Stiffness Method

约 1385 个字 3 张图片预计阅读时间 9 分钟

以下三种方法用于计算机编程

Matrix Partitioning

\[ \begin{bmatrix} K_{11}&K_{12} \\ K_{21}&K_{22} \end{bmatrix} \begin{Bmatrix} d_{fix} \\ d_{{?}} \end{Bmatrix} = \begin{Bmatrix} F_{?} \\ F_{fix} \end{Bmatrix} \]

用 \([\, ]_{fix}\) 表示已知位移或应力，用 \([\, ]_{?}\) 表示未知量，因此求解的步骤为：

求解： \(K_{22}d_{?} = F_{fix}-K_{21}d_{fix}\)
求解： \(F_? =K_{11}d_{fix}+K_{12}d_{?}\)

Note

如果此时已知量为 \(0\) （固定约束），我们可以删除对应行列的元素，比如说 \(d_{11}\) 位移为零，那么我们就可以删除第一行和第一列的元素，此时求解步骤为

\[ \begin{align} &K_{22} d_{?} = F_{fix} \\ \implies &F_{?} = K_{12}d_{?} \end{align} \]

这样方便求解

Advantages:
- 待求的方程比较少
- 满足特定约束
Disadvantages:
- 需要改变方程数量
- 不易编程

Row Substitution

假定约束条件给出 \(d_{i} = \delta\) ，则我们可以直接将其直接带入 Global Equation ：

\[ \begin{bmatrix} & & & \cdots & \\ K_{i_{1}} & K_{i_{2}} & \cdots & K_{ii} & \cdots \\ & & & \cdots & \end{bmatrix} \begin{Bmatrix} \\ \delta \\ \\ \end{Bmatrix} = \begin{Bmatrix} \\ F_{i} \\ \\ \end{Bmatrix} \]

同时保留位移信息

\[ \begin{bmatrix} & & & \cdots & \\ 0 & 0 & \cdots & 1 & \cdots \\ & & & \cdots & \end{bmatrix} \begin{Bmatrix} \\ d_{i} \\ \\ \end{Bmatrix} = \begin{Bmatrix} \\ \delta \\ \\ \end{Bmatrix} \]

Penalty Method

我们也可以将约束转换成一个比较大的惩罚项：

\[ \begin{bmatrix} & & & \cdots & \\ K_{i_{1}} & K_{i_{2}} & \cdots & K_{ii} +BIG& \cdots \\ & & & \cdots & \end{bmatrix} \begin{Bmatrix} \\ d_{i} \\ \\ \end{Bmatrix} = \begin{Bmatrix} \\ F_{i}+BIG \times\delta \\ \\ \end{Bmatrix} \]

展开后：

\[ \begin{align} \text{small} + (BIG)d_{i} &= \text{small} + BIG \times \delta \\ \implies \qquad d_{i } &= \delta \end{align} \]

一般取 \(BIG = 10^{15}(K_{ii})_{rep}\)

考虑两个弹簧的简单串联问题：

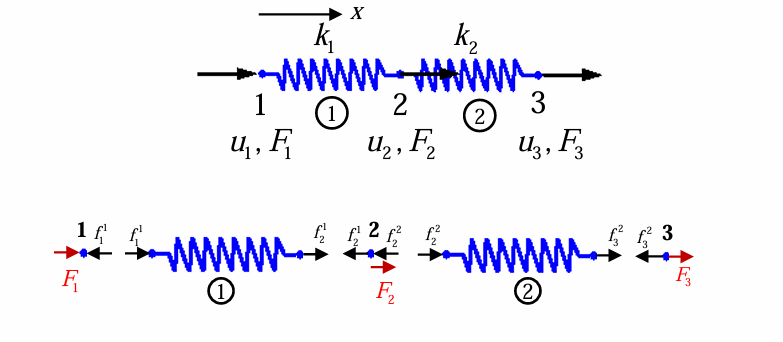
Pasted image 20250304135852.png

给出两个弹簧满足的平衡方程

\[ \begin{bmatrix} k_{1}&-k_{1} \\ -k_{1}&k_{1} \end{bmatrix} \begin{Bmatrix} u_{1} \\ u_{2} \end{Bmatrix} = \begin{Bmatrix} f_{1}^{1} \\ f_{2}^{1} \end{Bmatrix} \qquad \begin{bmatrix} k_{2}&-k_{2} \\ -k_{2}&k_{2} \end{bmatrix} \begin{Bmatrix} u_{2} \\ u_{3} \end{Bmatrix} = \begin{Bmatrix} f_{2}^{2} \\ f_{3}^{2} \end{Bmatrix} \]

考虑节点处的平衡条件可得装配后全局刚度矩阵：

\[ \begin{bmatrix} k_{1}&-k_{1} & 0 \\ -k_{1}&k_{1}+k_{2} & -k_{2} \\ 0 & -k_{2} & k_{2} \end{bmatrix} \begin{Bmatrix} u_{1} \\ u_{2} \\ u_{3} \end{Bmatrix} = \begin{Bmatrix} F_{1} \\ F_{2} \\ F_{3} \end{Bmatrix} \]

Note

如果通过组合元素刚度来创建全局刚度矩阵，\(k_{22}\) 是由作用于节点 2 的直接刚度之和给出，这是兼容性条件所要求的。 \(k_{ij}\) 一般是负的（反作用力）或者是零（无作用效果）

Tip

位置 \(ii\) 中的项由所有在节点 \(i\) 处汇合的元素的直接刚度总和组成
位置 \(ij\) 项由连接节点 \(i\) 和 \(j\) 的所有元素与节点 \(i\) 和 \(j\) 有关的间接刚度综合构成
反作用力项添加负值
为不发生相互作用的节点组合添加一个零

\(N\) 个自由度会产生一个 \(N\times N\) 的刚度矩阵（方阵）

（全局）刚度矩阵的 \(i\) 行与位移的积等于作用在系统第 \(i\) 个自由度的外力
刚度矩阵的第 \(j\) 列表示使 \(j\) 节点产生单位位移，其余节点不变所需要的力。
一般而言刚度矩阵为对称矩阵，对角线元素为正，矩阵为奇异矩阵

举个🌰

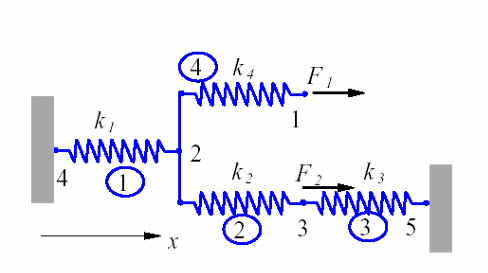
屏幕截图 2025-03-04 185842.png|300

考虑如图系统，对于节点 \((1)\) 直接刚度为 \(k_{4}\) ，节点 \((1)\) 和节点 \((2)\) 之间的连接弹簧刚度为 \(k_{4}\) 其作用效果为反作用力；对于节点 \((2)\) ，直接相连的弹簧有 \(k_{1},k_{2},k_{4}\) ，节点 \((2)\) 与节点 \((4)\) 之间的连接弹簧刚度为 \(k_{1}\) ，节点 \((2)\) 和节点 \((3)\) 之间的连接刚度弹簧节点为 \(k_{2}\)；对于节点 \((3)\) ，直接相连的弹簧有 \(k_{2},k_{3}\) ，除了节点 \((2)\) 外还与节点 \((5)\) 相连；对于节点 \((4)\) ，直接刚度为 \(k_{1}\) ，与节点 \((2)\) 相连；对于节点 \((5)\) ，直接刚度为 \(k_{3}\) ，与节点 \((3)\) 相连，所以全局刚度矩阵为

\[ \mathbf{K} = \begin{bmatrix} k_{4} & -k_{4} & 0 & 0 & 0 \\ -k_{4} & k_{4}+k_{2}+k_{1} & -k_{2} & -k_{1} & 0 \\ 0 & -k_{2} & k_{2}+k_{3} & 0 & -k_{3} \\ 0 & -k_{1} & 0 & k_{1} & 0 \\ 0 & 0 & -k_{3} & 0 & k_{3} \end{bmatrix} \]

还有一种求法，其思想与上面的两个弹簧装配问题类似，对于弹簧 \(k_{l}\) ，其两端节点的位移分别为 \(u_{i},u_{j}\) （\(i,j,l\) 不一定要相等），则此时局部刚度矩阵

\[ \mathbf{k}_{l} = \begin{bmatrix} k_{l} & -k_{l} \\ -k_{l} & k_{l} \end{bmatrix} \]

将其叠加就可得到全局装配矩阵

在这个例子中，对于弹簧 \({k}_{1}\) ，其作用两端节点位移为 \(u_{2},u_{4}\)；对于弹簧 \({k}_{2}\) ，其作用两端节点位移为 \(u_{2},u_{3}\)，对于弹簧 \({k}_{3}\) ，其作用两端节点位移为 \(u_{3},u_{5}\)；对于弹簧 \(k_{4}\) ，其作用两端节点位移为 \(u_{1},u_{2}\)，将其叠加可得全局刚度矩阵。

我们还能利用 Lagrange 方程或者能量最小原理得到上述方程。

由于刚度矩阵是一个奇异矩阵，也就是意味着其不可逆，\(\left\{ u \right\}\) 没有解。因此此时需要引入边界条件，从而将刚度矩阵变为一个可逆矩阵。

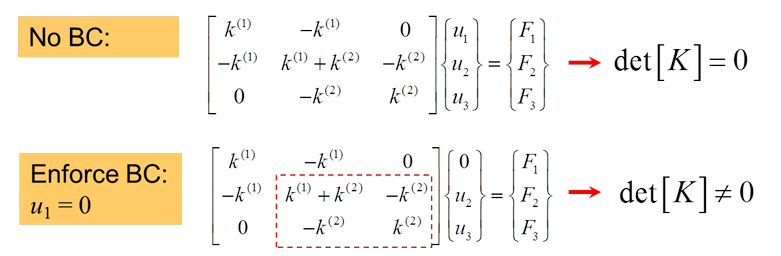
Pasted image 20250311191657.png

一个简单的例子就是，假定 \(u_{1}\) 为固定约束时，我们可以删去第一行和第一列的元素，剩下的元素构成一个刚度矩阵，如上图，变换后的刚度矩阵为

\[ [K] = \begin{bmatrix} k_{1}+k_{2} & -k_{2} \\ -k_{2} & k_{2} \end{bmatrix} \]

此时行列式 \(\det K = k_{1}k_{2}\) 变成一个可逆元素，系统存在唯一解。