Bar Beam and Plate
约 5493 个字 17 张图片 预计阅读时间 37 分钟
Bar
我们先推导局部(Local)坐标中杆单元方程
Features of a Bar
- 只受轴向力（tension or compressin）
- 沿轴向变形
- 不受剪力和弯矩
位移函数：
\[
\begin{align}
&u(x) = u_{i} + \frac{u_{j}-u_{i}}{L}x \\
\implies& u(x) = \left( 1-\frac{x}{L} \right) u_{i}+\frac{x}{L}u_{j} = \begin{bmatrix}
N_{i} & N_{j}
\end{bmatrix} \begin{Bmatrix}
u_{i} \\
u_{j}
\end{Bmatrix} \\
& \text{where} N_{i}=1-\frac{x}{L}\quad N_{j}= \frac{x}{L}
\end{align}
\]
\(N_{i},N_{j}\) 称为形函数，表示在定义域上元素假定位移函数的形状
应力和应变：
\[
\begin{align}
&\varepsilon = \frac{{\rm{d}} u }{{\rm {d}} x } =\frac{u_{j}-u_{i}}{L} \\
&\sigma = E\varepsilon = E \frac{u_{j}-u_{i}}{L}
\end{align}
\]
刚度矩阵：
\[
\frac{EA}{L}\begin{bmatrix}
1 & -1 \\
-1 & 1
\end{bmatrix}
\]
用能量法获取刚度矩阵：
- 位移
\[
u(x) =\begin{bmatrix}
N_{i} & N_{j}
\end{bmatrix} \begin{Bmatrix}
u_{i} \\
u_{j}
\end{Bmatrix} = [\mathbf{N}]\left\{\mathbf{u} \right\}
\]
- 应变
\[
\varepsilon_{x} = \frac{{\rm{d}} u(x) }{{\rm {d}} x } = \frac{{\rm{d}} [\mathbf{N}] }{{\rm {d}} x }\left\{\mathbf{u} \right\} = \left[ \mathbf{B} \right] \left\{\mathbf{u} \right\}
\]
- 应力
\[
\sigma_{x} =E\varepsilon_{x} = [\mathbf{D}][\mathbf{B}]\left\{\mathbf{u} \right\} \quad [\mathbf{D}]=[E]
\]
应变矩阵 \([\mathbf{B}]\) 计算了节点位移而产生的应变，材料性质矩阵 \([\mathbf{D}]\) 一般是一个对称矩阵。
杆的势能
\[
\Pi _{p}(u) = U(u)+\Omega(u)
\]
其中 \(U\) 为应变能，在杆的问题中为：
\[
\begin{align}
U(u)&=\frac{1}{2}\iiint_{V}\sigma_{x}\varepsilon_{x}dV \\
&=\frac{A}{2}\int_{0}^{L}\sigma_{x}^{T}\varepsilon_{x}\mathrm{d}x = \frac{A}{2}\int_{0}^{L} \left\{\mathbf{u} \right\}^{T}[\mathbf{B}]^{T}[\mathbf{D}]^{T}[\mathbf{B}]\left\{\mathbf{u} \right\}\mathrm{d}x \\
&=\frac{AL}{2} \left\{\mathbf{u} \right\}^{T}[\mathbf{B}]^{T}[\mathbf{D}]^{T}[\mathbf{B}]\left\{\mathbf{u} \right\}
\end{align}
\]
\(\Omega\) 是功，
\[
\begin{align}
\Omega &= -\left( f_{i}u_{i}+f_{j}u_{j} \right) -\underbrace{\iint_{S_{1}}u_{s}^{T}T_{x}dS}_{表面载荷作用} \\
&=-\left\{\mathbf{u} \right\}^{T}\left\{ \mathbf{P} \right\}-\iint_{S_{1}}\left\{\mathbf{u} \right\}^{T}\left[ \mathbf{N}_{s} \right]^{T}T_{x}\mathrm{d}S \\
&=-\left\{\mathbf{u} \right\}^{T}\left\{ \mathbf{f} \right\} \\
&\quad \left\{ \mathbf{f} \right\} = \left\{ \mathbf{{P}} \right\}+\underset{ 等效节点力 }{ \iint_{S_{1}}\left[ \mathbf{N}_{s} \right]^{T}T_{x}\mathrm{d}S }
\end{align}
\]
因此势能可写作
\[
\Pi_{p}=\frac{AL}{2} \left\{\mathbf{u} \right\}^{T}[\mathbf{B}]^{T}[\mathbf{D}]^{T}[\mathbf{B}]\left\{\mathbf{u} \right\}-\left\{\mathbf{u} \right\}^{T}\left\{ \mathbf{f} \right\}
\]
由最小势能原理可得
\[
\frac{\partial \Pi_{p} }{\partial \left\{ \mathbf{u} \right\} } \implies AL \left[ \mathbf{B} \right] ^{T}\left[ \mathbf{D} \right] ^{T}\left[ \mathbf{B} \right] \left\{ \mathbf{u} \right\} =\left\{\mathbf{f} \right\} \triangleq[\mathbf{k}] \left\{ \mathbf{u} \right\}=\left\{ \mathbf{f} \right\}
\]
将均布载荷转换成节点上的集中力。
\[
\begin{align}
&\left\{ \mathbf{f }_{s} \right\} =\iint_{S_{1}}\left[ \mathbf{N}_{s} \right]^{T}T_{x}dS \\
\text{Here }& \left[ \mathbf{N}_{s} \right] =\begin{bmatrix}
1-x/L & x/L
\end{bmatrix},\quad T_{x} = q ,\quad dS =dx \\
\implies& \left\{ \mathbf{f}_{s} \right\} =\iint_{S_{1}} \left[ \mathbf{N}_{s} \right]^{T}T_{x}dS = q\int_{0}^{L}\begin{Bmatrix}
1-x/L \\
x/L
\end{Bmatrix} \, {\rm d} x = \begin{Bmatrix}
qL /2 \\
qL /2
\end{Bmatrix}
\end{align}
\]
这是为了在运用 \(\mathbf{Ku=F}\) 的时候能确定节点上对应的集中力
在比如说，假定杆上的载荷服从线性关系，即 \(\hat{T}_{x}= C \hat{x}\) ，那么作用在前后节点上的集中力为
\[
\left\{ \mathbf{f}_{s} \right\} =\iint_{S_{1}} \left[ \mathbf{N}_{s} \right]^{T}T_{x}dS = q\int_{0}^{L}\begin{Bmatrix}
1-x/L \\
x/L
\end{Bmatrix} Cx\, {\rm d} x = \begin{Bmatrix}
CL^{2} /6 \\
CL^{2} /3
\end{Bmatrix}
\]
Example
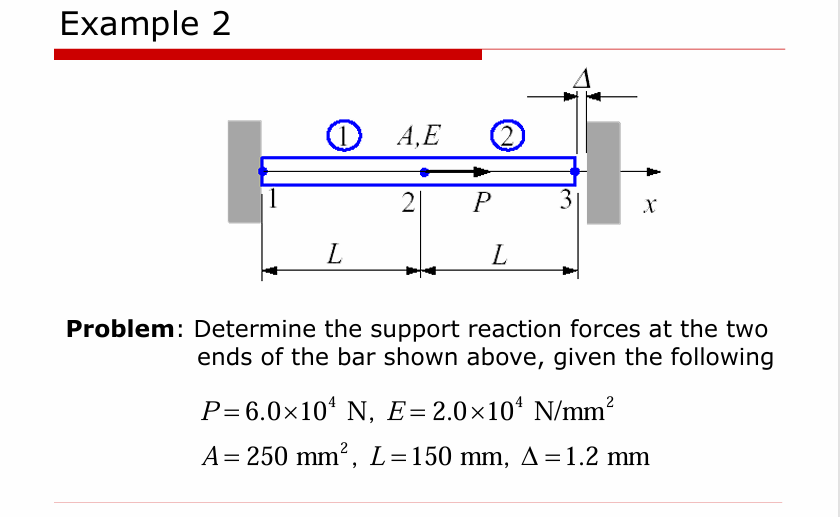
我们先考虑杆会不会接触到墙面，当右端没有墙时，\(3\) 点位移为
\[
\Delta_{0} = \frac{PL}{EA} = 1.8\mathrm{mm}> 1.2 \mathrm{mm}
\]
所以杆会接触到墙壁。
Global 刚度矩阵：
\[
\mathbf{K} =\frac{EA}{L}\begin{bmatrix}
1 & -1 & 0 \\
-1 & 2 & -1 \\
0 & -1 & 1
\end{bmatrix}
\]
所以待定方程为：
\[
\frac{EA}{L}\begin{bmatrix}
1 & -1 & 0 \\
-1 & 2 & -1 \\
0 & -1 & 1
\end{bmatrix}\begin{Bmatrix}
u_{1} \\
u_{2} \\
u_{3}
\end{Bmatrix}= \begin{Bmatrix}
F_{1} \\
F_{2} \\
F_{3}
\end{Bmatrix}
\]
边界条件：
\[
u_{1}= 0,u_{3} =\Delta,F_{2} = P
\]
可以解得
\[
u_{2} = \frac{1}{2}\left( \frac{PL}{EA}+\Delta \right)=1.5 \mathrm{ mm}
\]
收敛性
- 位移在每个节点（node）上都是准确的，但是在节点之间不一定
- 每个元素(elements)所受的应力为常量，但是元素之间的应力不是连续的
- 解的准确性会随着元素数量的增加而提高
在FEA 中，我们采用多项式来描述一个元素的位移。
\[
\begin{align}
u(x,y,z) &= a_{0} +a_{1} x+b_{1} y +c_{1}z+\dots \\
&= N_{1}(x,y,z) u_{1}+N_{2}(x,y,z)u_{2}+\dots \\
& = \sum_{i}^{} N_{i}u_{i}
\end{align}
\]
形函数的性质： 1. 在节点 \(i,N_{i} = 1\)，在其他节点 \(N_{i}= 0\) 2. 允许刚体移动：\(\sum_{}^{}N_{i}=1\)
位移函数的完整性和相容性确保 FEA 的收敛性
- 完备性（Complete）：allow for a rigid-body displacement and a constant strain within the element
- 相容性（Compatible）：continuity between adjacent elements and within the elemen
- \(C^{m}\) 描述了多项式的连续程度，比如说 \(C^{0}\) 表述位移式连续的，\(C^{1}\) 表述位移和其一阶导数是连续的。
复杂杆
将局部(Local)元素和全局(Global)元素联系起来
取元素与水平方向的夹角为 \(\theta\) ，即定义
\[
C= \cos \theta = \frac{X_{j}-X_{i}}{L}\quad S =\sin \theta =\frac{Y_{j}-Y_{i}}{L}
\]
取 \(u'\) 表示局部元素，\(u\) 为全局元素，则坐标系的变换满足：
\[
\begin{Bmatrix}
u_{i}' \\
v_{i} '\\
u_{j} '\\
v_{j}'
\end{Bmatrix}
=\begin{bmatrix}
C & S & 0 & 0 \\
-S & C & 0 & 0 \\
0 & 0 & C & S \\
0 & 0 & -S & C
\end{bmatrix}\begin{Bmatrix}
u_{i} \\
v_{i} \\
u_{j} \\
v_{j}
\end{Bmatrix}\triangleq \mathbf{u}' = \mathbf{Tu}
\]
称 \(\mathbf{T}\) 为变换矩阵，其满足 \(\mathbf{T}^{-1}=\mathbf{T}^{T}\)
节点上的力也遵循变换规则
\[
\mathbf{f}' = \mathbf{Tf}
\]
对应刚度矩阵
\[
\mathbf{k}=\mathbf{T}^{T}\mathbf{k}'\mathbf{T}
\]
展开为
\[
\mathbf{k}=\frac{EA}{L}\begin{bmatrix}
C^{2} & CS & -C^{2} & -CS \\
CS & S^{2} & -CS & -S^{2} \\
-C^{2} & -CS & C^{2} & CS \\
-CS & -S^{2} & CS & S^{2}
\end{bmatrix}
\]
注：每一根杆都有自己的旋转矩阵
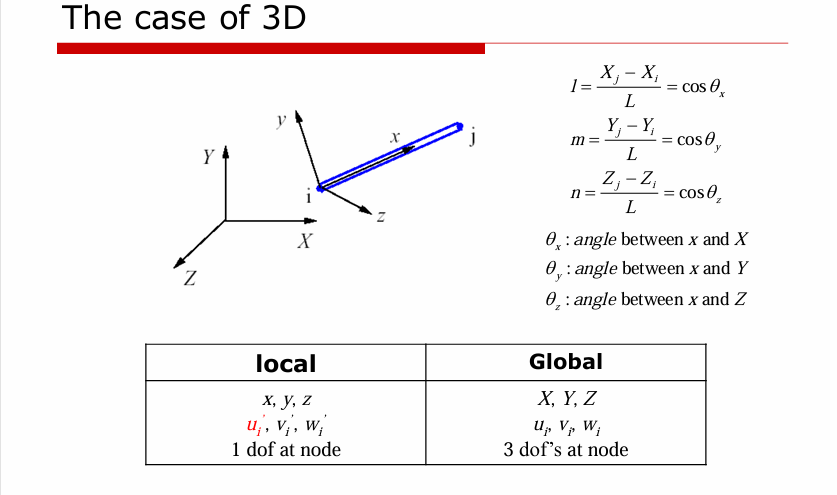
如果全局元素是一个三维问题，则取
\[
\begin{align}
l& = \frac{X_{j}-X_{i}}{L}= \cos \theta_{x} \\
m& = \frac{Y_{j}-Y_{i}}{L}= \cos \theta_{y} \\
n& = \frac{Z_{j}-Z_{i}}{L}= \cos \theta_{z}
\end{align}
\]
则刚度矩阵为
\[
\left[ \mathbf{k} \right] = \frac{AE}{L}\begin{bmatrix}
l^{2} & lm & ln & -l^{2} & -lm & -ln \\
lm & m^{2} & mn & -lm & -m^{2} & -mn \\
ln & mn & n^{2} & -ln & -mn & -n^{2} \\
-l^{2} & -lm & -ln & l^{2} & lm & ln \\
-lm & -m^{2} & -mn & lm & m^{2} & mn \\
-ln & -mn & -n^{2} & ln & mn & n^{2}
\end{bmatrix}
\]
Example
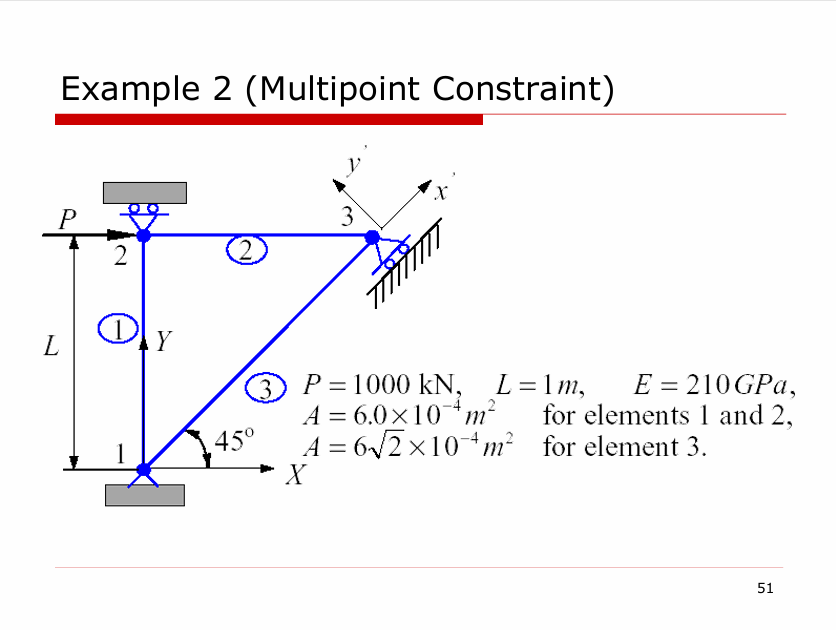
对于杆 \(1\) ，\(\theta = 90^{\circ},C= 0,S=1\) ，对应的 Global 刚度矩阵：
\[
\mathbf{k}_{1} = \frac{EA}{L}\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 1 & 0 & -1 \\
0 & 0 & 0 & 0 \\
0 & -1 & 0 & 1
\end{bmatrix}
\]
对于杆 \(2\) \(\theta =0^{\circ},C=1,S=0\)，对应的 Global 刚度矩阵：
\[
\mathbf{k}_{2} = \frac{EA}{L} \begin{bmatrix}
1 & 0 & -1 & 0 \\
0 & 0 & 0 & 0 \\
-1 & 0 & 1 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
\]
对于杆 \(3,\theta =45^{\circ},C = \sqrt{ 2 } /2,S =\sqrt{ 2 } /2\) 对应的 Global 刚度矩阵
\[
\mathbf{k}_{3} =\frac{EA}{L}\begin{bmatrix}
0.5 & 0.5 & -0.5 & -.05 \\
0.5 & 0.5 & -0.5 & -0.5 \\
-0.5 & -0.5 & 0.5 & 0.5 \\
-0.5 & -0.5 & 0.5 & 0.5
\end{bmatrix}
\]
装配后的矩阵
\[
\frac{EA}{L}
\begin{bmatrix}
0.5 & 0.5 & 0 & 0 & -0.5 & -0.5 \\
0.5 & 1.5 & 0 & -1 & -0.5 & -0.5 \\
0 & 0 & 1 & 0 & -1 & 0 \\
0 & -1 & 0 & 1 & 0 & 0 \\
-0.5 & -0.5 & -1 & 0 & 1.5 & 0.5 \\
-0.5 & -0.5 & 0 & 0 & 0.5 & 0.5
\end{bmatrix}
\begin{Bmatrix}
u_{1} \\
v_{1} \\
u_{2} \\
v_{2} \\
u_{3} \\
v_{3} \\
\end{Bmatrix}
=\begin{Bmatrix}
F_{1X} \\
F_{1Y} \\
F_{2X} \\
F_{2Y} \\
F_{3X} \\
F_{3Y}
\end{Bmatrix}
\]
引入边界条件，此时有两个特殊的边界条件：\(v_{3}' =0,F_{3x'}=0\)，对应几何关系
\[
\begin{align}
u_{3}-v_{3} &= 0 \\
F_{3X}-F_{3Y} &= 0
\end{align}
\]
其余边界条件： \(u_{1} =v_{1}=v_{2} =0,F_{2X}=P\) ，对应待定方程：
\[
\frac{EA}{L}\begin{bmatrix}
1 & -1 & 0 \\
-1 & 1.5 & 0.5\\
0 & 0.5 & 0.5
\end{bmatrix}\begin{Bmatrix}
u_{2} \\
u_{3} \\
u_{3}
\end{Bmatrix}=
\begin{Bmatrix}
P \\
F_{3X} \\
F_{3X}
\end{Bmatrix}
\]
带入求解即可
Beam
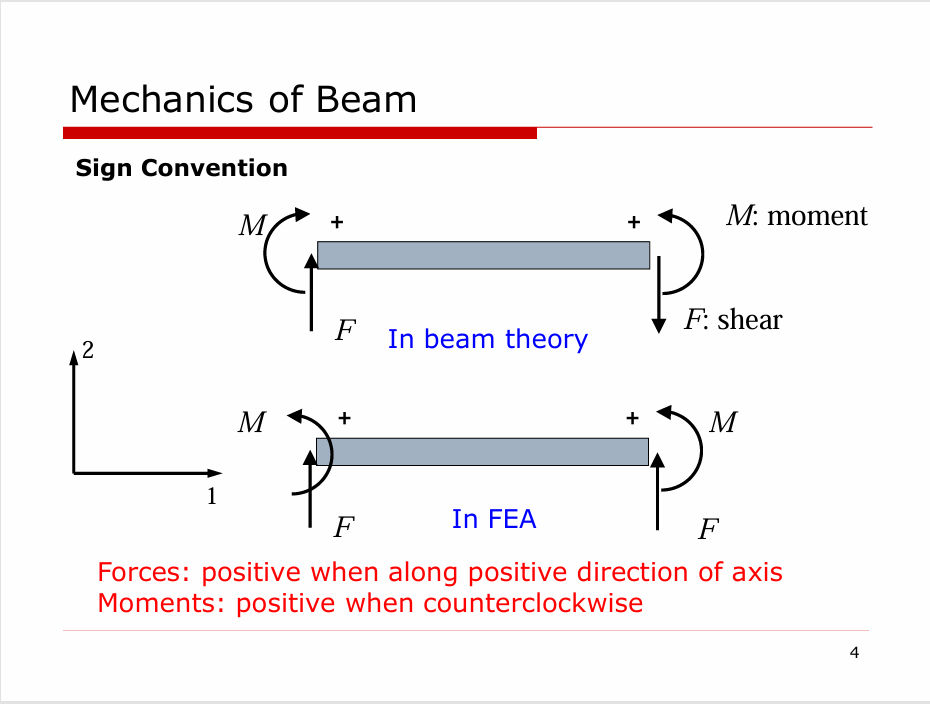
与材料力学中不同，在有限元方法中，我们定义力沿坐标轴正方向为正，力矩逆时针为正
- 挠曲线： \(v(x,t)\)
- 转角：\(\theta = \frac{\partial v}{\partial x}\)
- 弯矩： \(M(x,t) = E(x)I(x)\frac{\partial^2 v}{\partial^2 x}\)
- 剪力：\(P(x,t) = \frac{\partial M}{\partial x}\)
- 分布力：\(f(x,t) =\frac{\partial P}{\partial x}\)
对于一个梁单元，其有四个自由度（两端挠度和转角）
挠度
\[
v(x) = a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}
\]
引入边界条件：
\[
\begin{align}
v(0) = v_{i}&,v(L)= v_{j } \\
\frac{{\rm{d}} v }{{\rm {d}} x }(x=0) = \theta_{i}&,\frac{{\rm{d}} v }{{\rm {d}} x }(x=L)=\theta_{j}
\end{align}
\]
解得：
\[
\begin{align}
&a_{0}=v_{i} \\
&a_{1} = \theta i \\
&a_{2} = -\frac{3}{L^{2}}(v_{i}-v)-\frac{1}{L}(2\theta_{i}+\theta_{j}) \\
&a_{3} = \frac{2}{L}(v_{i}-v_{j})+\frac{1}{L^{2}}(\theta_{i}+\theta_{j})
\end{align}
\]
型函数
\[
v=N_{1}v_{i}+N_{2}\theta_{i}+N_{3}v_{j}+N_{4}\theta_{j}
\]
\[
\begin{align}
&N_{1}(x)=1-3 \frac{x^{2}}{L^{2}}+2\frac{x^{3}}{L^{3}} \\
&N_{2}(x) = x - 2\frac{x^{2}}{L}+\frac{x^{3}}{L^{2}} \\
&N_{3}(x)=3\frac{x^{2}}{L^{2}}-2 \frac{x^{3}}{L^{3}} \\
&N_{4}(x) =- \frac{x^{2}}{L}+ \frac{x^{3}}{L^{2}}
\end{align}
\]
Tip
注意前面所讲，FEM 给出的解在节点上是准确的，但是节点和节点之间不一定是准确的，对于受均布载荷的梁方程，根据常微分理论对应位移函数应该是一个四次多项式，型函数给出的位移解最多为三次多项式。
待定方程
\[
\frac{EI}{L^{3}}\begin{bmatrix}
12 & 6L & -12 & 6L \\
6L & 4L^{2} & -6L & 2L^{2} \\
-12 & -6L & 12 & -6L \\
6L & 2L^{2} & -6L & 4L^{2}
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
\theta_{i} \\
v_{j} \\
\theta_{j} \\
\end{Bmatrix}
=\begin{Bmatrix}
F_{i} \\
M_{i} \\
F_{j} \\
M_{j}
\end{Bmatrix}
\]
能量法求解平衡方程
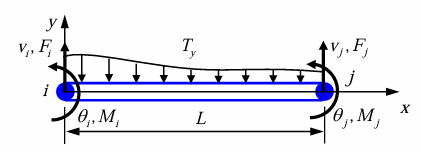
对挠度取二阶导数
\[
\frac{{\rm{d}} ^{2}v }{{\rm {d}} x^{2} } = \frac{{\rm{d}} ^{2} }{{\rm {d}} x^{2} } (\mathbf{Nu})=\mathbf{Bu}
\]
其中
\[
\begin{align}
\mathbf{B}&= \frac{{\rm{d}} ^{2} }{{\rm {d}} x^{2} } \mathbf{N} = \begin{bmatrix}
N_{1}'' & N_{2}'' & N_{3}'' & N_{4}''
\end{bmatrix} \\
&=\begin{bmatrix}
-\frac{6}{L^{2}}+\frac{12x}{L^{3}} & -\frac{4}{L}+\frac{6x}{L^{2}} & \frac{6}{L^{2}}-\frac{12x}{L^{3}} & -\frac{2}{L}+\frac{6x}{L^{2}}
\end{bmatrix}
\end{align}
\]
应力应变:
\[
\begin{align}
&\varepsilon_{x} = -y \frac{{\rm{d}} ^{2} v}{{\rm {d}} x^{2} } -y\mathbf{Bu} \\
&\sigma_{x}=E\varepsilon_{x} = - yE\mathbf{Bu}
\end{align}
\]
应变能：
\[
\begin{align}
U&=\frac{1}{2}\iiint_{V}\sigma_{x}\varepsilon_{x}dV =\frac{1}{2}\int_{x}\iint_{A}\sigma_{x}^{T}\varepsilon_{x}\,\mathrm{d}A\mathrm{dx} \\
&=\frac{1}{2}\int_{x}\iint_{A}y^{2}\mathbf{u}^{T}\mathbf{B}^{T}E\mathbf{Bu}\, \mathrm{d}A\mathrm{d}x = \frac{1}{2}\mathbf{u}^{T}\int_{0}^{L}\mathbf{B}^{T}EI\mathbf{B}\,\mathrm{d}x\mathbf{u}
\end{align}
\]
外力施加的势能
\[
\Omega = -\mathbf{u}^{T}\mathbf{p}-\iint_{S}\mathbf{u}^{T}\mathbf{N}_{s}^{T}T_{y}dS = -\mathbf{u}^{T}\mathbf{p}-\mathbf{u}^{T}\int_{0}^{L} \mathbf{N}_{s}^{T}bT_{y} \, {\rm d} x
\]
最小势能原理给出
\[
\begin{align}
&\frac{\delta(U+\Omega)}{\delta \mathbf{u}^{T}}=0 \\
\implies&\left(\int_{0}^{L}\mathbf{B}^{T}EI\mathbf{B}\,\mathrm{d}x\right)\mathbf{u} = \mathbf{p}+\int_{0}^{L} \mathbf{N}_{s}^{T}bT_{y} \, {\rm d} x
\end{align}
\]
一般取 \(bT_{y}\) 为作用在梁上的载荷或力
Example
将一个均布载荷转换成了作用在节点上的力和弯矩:
\[
\int_{0}^{L} \mathbf{N}_{s}^{T}bT_{y} \, {\rm d} x = \int_{0}^{L} \mathbf{N}_{s}^{T}q \, {\rm d} x = q \int_{0}^{L}\begin{Bmatrix}
1-3 \frac{x^{2}}{L^{2}}+2\frac{x^{3}}{L^{3}} \\
x - 2\frac{x^{2}}{L}+\frac{x^{3}}{L^{2}} \\
3\frac{x^{2}}{L^{2}}-2 \frac{x^{3}}{L^{3}} \\
- \frac{x^{2}}{L}+ \frac{x^{3}}{L^{2}}
\end{Bmatrix}dx = \begin{Bmatrix}
\frac{qL}{2} \\
\frac{qL^{2}}{12} \\
\frac{qL}{2} \\
-\frac{qL^{2}}{12}
\end{Bmatrix}
\]
Example
对于作用在梁上一点的力，我们可以采用 Dirac 函数 处理。对于上述情况，在梁上 \(x= \frac{L}{2}\) 处作用力 \(F= P\) ，取 \(\delta\) 函数 \(\delta\left( \frac{L}{2} \right)\) ，则
\[
\int_{0}^{L} \mathbf{N}_{s}^{T}P\delta\left( \frac{L}{2} \right) \, {\rm d} x = P\int_{0}^{L}\delta \left( \frac{L}{2} \right) \begin{Bmatrix}
1-3 \frac{x^{2}}{L^{2}}+2\frac{x^{3}}{L^{3}} \\
x - 2\frac{x^{2}}{L}+\frac{x^{3}}{L^{2}} \\
3\frac{x^{2}}{L^{2}}-2 \frac{x^{3}}{L^{3}} \\
- \frac{x^{2}}{L}+ \frac{x^{3}}{L^{2}}
\end{Bmatrix}dx = \begin{Bmatrix}
-\frac{P}{2} \\
-\frac{PL}{8} \\
-\frac{P}{2} \\
\frac{PL}{8}
\end{Bmatrix}
\]
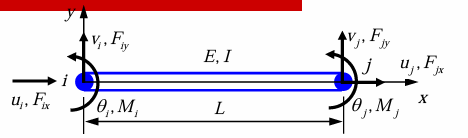
如果梁上作用横向力，则引入轴向的自由度（也就是在上述梁分析方法的基础上增加杆的分析），此时自由度为 \(6\) ，对应刚度矩阵方程：
\[
\begin{bmatrix}
\frac{EA}{L} & 0 & 0 & -\frac{EA}{L} & 0 & 0 \\
0 & \frac{12EI}{L^3} & \frac{6EI}{L^2} & 0 & -\frac{12EI}{L^3} & \frac{6EI}{L^2} \\
0 & \frac{6EI}{L^2} & \frac{4EI}{L} & 0 & -\frac{6EI}{L^2} & \frac{2EI}{L} \\
-\frac{EA}{L} & 0 & 0 & \frac{EA}{L} & 0 & 0 \\
0 & -\frac{12EI}{L^3} & -\frac{6EI}{L^2} & 0 & \frac{12EI}{L^3} & -\frac{6EI}{L^2} \\
0 & \frac{6EI}{L^2} & \frac{2EI}{L} & 0 & -\frac{6EI}{L^2} & \frac{4EI}{L}
\end{bmatrix}\begin{Bmatrix}
u_{i} \\
v_{i} \\
\theta_{i} \\
u_{j} \\
v_{j} \\
\theta_{j}
\end{Bmatrix}=
\begin{Bmatrix}
F_{ix} \\
F_{iy} \\
M_i \\
F_{jx} \\
F_{jy} \\
M_j
\end{Bmatrix}
\]
Tip
如果梁的某一端为弹性支撑（弹簧），其自由度为 4 （梁的自由度）+ 1(弹簧的自由度) = 5 ,我们依旧可以装配法装配我们的刚度矩阵
Example
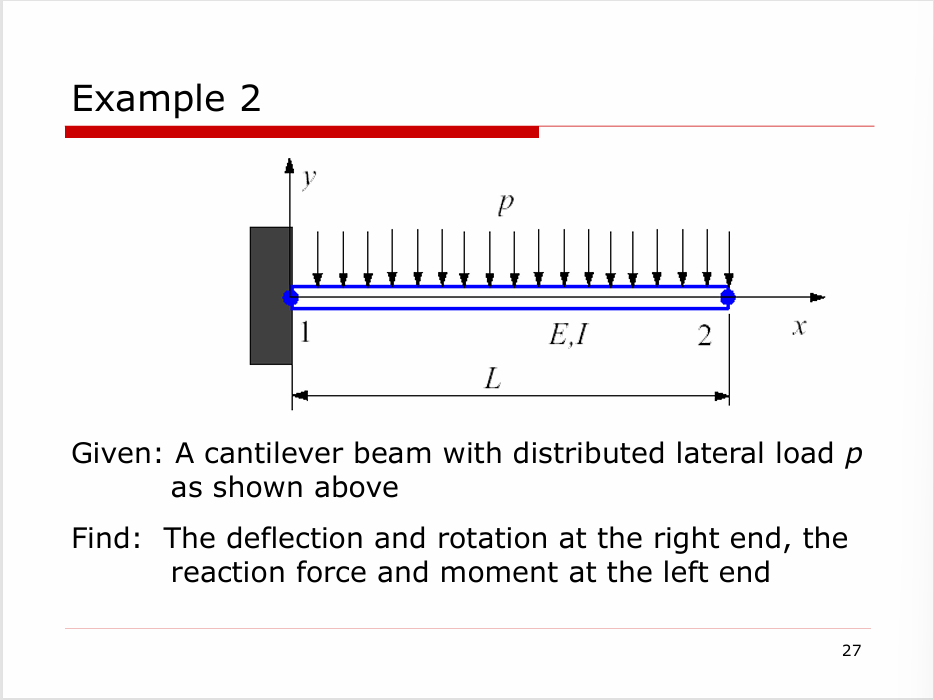先将均布载荷转换成作用在节点上的力和力矩。取 \(F_{2y}=-f,M_{2}=m,\left( f=\frac{pL}{2},m = \frac{pL^{2}}{12} \right)\) ，刚度矩阵方程
\[\begin{align}
&\frac{EI}{L^{3}}\begin{bmatrix}
12 & 6L & -12 & 6L \\
6L & 4L^{2} & -6L & 2L^{2} \\
-12 & -6L & 12 & -6L \\
6L & 2L^{2} & -6L & 4L^{2}
\end{bmatrix}\begin{Bmatrix}
0\\
0\\
v_{2} \\
\theta_{2} \\
\end{Bmatrix}
=\begin{Bmatrix}
F_{1y} \\
M_{1} \\
-f \\
m
\end{Bmatrix} \\
\implies & \frac{EI}{L^{3}}\begin{bmatrix}
12 & -6L \\
-6L & 4L^{2}
\end{bmatrix} \begin{Bmatrix}
v_{2} \\
\theta_{2}
\end{Bmatrix} = \begin{Bmatrix}
-f \\
m
\end{Bmatrix} \\
\implies& \begin{Bmatrix}
v_{2} \\
\theta_{2}
\end{Bmatrix} =\begin{Bmatrix}
-\frac{pL^{4}}{8EI} \\
-\frac{pL^{3}}{6EI}
\end{Bmatrix}
\end{align}
\]
如果要求取作用在作用在 \(1\) 处的反作用力，先求取 \(F_{1y},M_{1}\)
\[
\begin{Bmatrix}
F_{1y} \\
M_{1}
\end{Bmatrix}= \frac{EI}{L^{3}}\begin{bmatrix}
-12 & 6L \\
-6L & 2L^{2}
\end{bmatrix}\begin{Bmatrix}
v_{2} \\
\theta_{2}
\end{Bmatrix} = \begin{Bmatrix}
\frac{pL}{2} \\
\frac{5pL^{2}}{12}
\end{Bmatrix}
\]
但注意此时求出来的是在节点 \(1\) 总的作用力，要扣除均布载荷的作用效果
\[
\begin{Bmatrix}
F'_{1y} \\
M_{1}
\end{Bmatrix} = \begin{Bmatrix}
\frac{pL}{2} \\
\frac{5pL^{2}}{12}
\end{Bmatrix}- \begin{Bmatrix}
-\frac{pL}{2} \\
-\frac{pL^{2}}{12}
\end{Bmatrix}= \begin{Bmatrix}
{pL} \\
\frac{pL^{2}}{2}
\end{Bmatrix}
\]
考虑带有铰链的梁，铰链使得梁在铰接处的斜率不连续。因此，我们将其拆分成两个部分，将铰接点归入某一部分处理，构造一个新的刚度矩阵，而对于另一部分，由于不包含铰接点，所以视作正常的梁问题
先考虑右端的梁，对于铰接处，其满足 \(\theta_{j}\neq 0,M_{j}=0\) ，由于作用在节点的弯矩为零，做如下分块矩阵
\[
\frac{EI}{L^{3}}\left[\begin{array}{ccc:c}
12 & 6L & -12 & 6L \\
6L & 4L^{2} & -6L & 2L^{2} \\
-12 & -6L & 12 & -6L \\
\hdashline
6L & 2L^{2} & -6L & 4L^{2}
\end{array}
\right]\begin{Bmatrix}
v_{i} \\
\theta_{i} \\
v_{j} \\
\hdashline\theta_{j} \\
\end{Bmatrix}
=\begin{Bmatrix}
F_{i} \\
M_{i} \\
F_{j} \\
\hdashline M_{j}=0
\end{Bmatrix}
\]
简写成如下形式
\[
\begin{bmatrix}
K_{11} & K_{12} \\
K_{21} & K_{22}
\end{bmatrix}\begin{Bmatrix}
d_{1} \\
d_{2}
\end{Bmatrix}
= \begin{Bmatrix}
f_{1} \\
f_{2}=0
\end{Bmatrix}
\]
可以解得
\[
\begin{align}
d_{2} &= K_{22}^{-1}(f_{2}-K_{21}d_{1}) \\
(K_{11}-K_{12}K^{-1}_{22}K_{21})d_{1}&= f_{1}
\end{align}
\]
有第二个式子可以推出
\[
\frac{3EI}{L^{3}}\begin{bmatrix}
1 & L & -1 \\
L & L^{2} & -L \\
-1 & -L & 1
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
\theta_{i} \\
v_{j}
\end{Bmatrix} =\begin{Bmatrix}
F_{iy} \\
M_{i} \\
F_{jy}
\end{Bmatrix}
\]
扩展成刚度矩阵（这是为了后面能够装配全局刚度矩阵，但是要保持 \(M_{j}=0\) ）
\[
\frac{3EI}{L^{3}}\begin{bmatrix}
1 & L & -1 & 0\\
L & L^{2} & -L & 0\\
-1 & -L & 1 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
\theta_{i} \\
v_{j} \\
\theta_{j}
\end{Bmatrix} =\begin{Bmatrix}
F_{iy} \\
M_{i} \\
F_{jy} \\
M_{j}
\end{Bmatrix}
\]
如果我们将铰接点归入左端处理的话，则上两个方程改为：
\[
\frac{3EI}{L^{3}}\begin{bmatrix}
1 & -1 & L \\
-1 & 1 & -L \\
L & -L & L^{2}
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
v_{j}\\
\theta_{j} \\
\end{Bmatrix} =\begin{Bmatrix}
F_{iy} \\
F_{jy} \\
M_{j} \\
\end{Bmatrix}
\]
\[
\frac{3EI}{L^{3}}\begin{bmatrix}
1 &0 & -1 & L \\
0 & 0 & 0 & 0 \\
-1 &0 & 1 & -L \\
L & 0 & -L & L^{2}
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
\theta_{i} \\
v_{j}\\
\theta_{j} \\
\end{Bmatrix} =\begin{Bmatrix}
F_{iy} \\
M_{i} \\
F_{jy} \\
M_{j} \\
\end{Bmatrix}
\]
Example
我们将铰链归入右端，则可以写出
\[
\mathbf{k_{1}=}\frac{3EI}{a^{3}}\begin{bmatrix}
1 & a & -1 & 0\\
a & a^{2} & -a & 0\\
-1 & -a & 1 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
\]
\[
\mathbf{k}_{2} = \frac{EI}{b^{3}}\begin{bmatrix}
12 & 6b & -12 & 6b \\
6b & 4b^{2} & -6b & 2b^{2} \\
-12 & -6b & 12 & -6b \\
6b & 2b^{2} & -6b & 4b^{2}
\end{bmatrix}
\]
装备后的刚度矩阵方程
\[
EI \begin{bmatrix}
\frac{3}{a^3} & \frac{3}{a^2} & -\frac{3}{a^3} & 0 & 0 & 0 \\
\frac{3}{a^2} & \frac{3}{a} & -\frac{3}{a^2} & 0 & 0 & 0 \\
-\frac{3}{a^3} & -\frac{3}{a^2} & \frac{3}{a^3} + \frac{12}{b^3} & \frac{6}{b^2} & \frac{12}{b^3} & \frac{6}{b^2} \\
0 & 0 & \frac{6}{b^2} & \frac{4}{b} & -\frac{6}{b^2} & \frac{2}{b} \\
0 & 0 & -\frac{12}{b^3} & -\frac{6}{b^2} & \frac{12}{b^3} & -\frac{6}{b^2} \\
0 & 0 & \frac{6}{b^2} & \frac{2}{b} & -\frac{6}{b^2} & \frac{4}{b}
\end{bmatrix}
\begin{Bmatrix}
v_1 \\
\theta_1 \\
v_2 \\
\theta_2 \\
v_3 \\
\theta_3
\end{Bmatrix}
=
\begin{Bmatrix}
F_{1y} \\
M_1 \\
F_{2y} \\
M_2 \\
F_{3y} \\
M_3
\end{Bmatrix}
\]
引入边界条件，解出
\[
\begin{Bmatrix}
v_{2} \\
\theta_{2}
\end{Bmatrix}
=\begin{Bmatrix}
-a^{3}b^{3}P / [3(b^{3}+a^{3})EI] \\
a^{3}b^{2}P / [2(b^{3}+a^{3})EI]
\end{Bmatrix}
\]
复杂梁
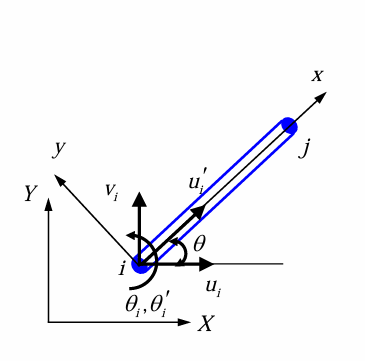
与杆类似，梁的二维变换满足：
\[
\begin{Bmatrix}
u_{i}' \\
v_{i} '\\
\theta_{i}'\\
u_{j} '\\
v_{j}' \\
\theta_j'
\end{Bmatrix}
=\begin{bmatrix}
C & S & 0 & 0 & 0 & 0 \\
-S & C & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0& C & S & 0\\
0 & 0 & 0 & -S & C & 0 \\
0 & 0 & 0 & 0 & 0 & 1
\end{bmatrix}\begin{Bmatrix}
u_{i} \\
v_{i} \\
\theta_{i} \\
u_{j} \\
v_{j} \\
\theta_{j}
\end{Bmatrix}\triangleq \mathbf{u}'=\mathbf{Tu}
\]
同样的我们有： \(\mathbf{f}'=\mathbf{Tf}\)
刚度矩阵方程
\[
\begin{bmatrix}
\frac{EA}{L} & 0 & 0 & -\frac{EA}{L} & 0 & 0 \\
0 & \frac{12EI}{L^3} & \frac{6EI}{L^2} & 0 & -\frac{12EI}{L^3} & \frac{6EI}{L^2} \\
0 & \frac{6EI}{L^2} & \frac{4EI}{L} & 0 & -\frac{6EI}{L^2} & \frac{2EI}{L} \\
-\frac{EA}{L} & 0 & 0 & \frac{EA}{L} & 0 & 0 \\
0 & -\frac{12EI}{L^3} & -\frac{6EI}{L^2} & 0 & \frac{12EI}{L^3} & -\frac{6EI}{L^2} \\
0 & \frac{6EI}{L^2} & \frac{2EI}{L} & 0 & -\frac{6EI}{L^2} & \frac{4EI}{L}
\end{bmatrix}
\begin{Bmatrix}
u_{i}' \\
v_{i} '\\
\theta_{i}'\\
u_{j} '\\
v_{j}' \\
\theta_j'
\end{Bmatrix}
=\begin{Bmatrix}
F_{ix} '\\
F_{iy} '\\
M_i '\\
F_{jx}' \\
F_{jy} '\\
M_j'
\end{Bmatrix}\triangleq \mathbf{k}'\mathbf{u}' = \mathbf{f'}
\]
可得刚度变换矩阵：
\[
\mathbf{k} = \mathbf{T}^{T}\mathbf{k'T}
\]
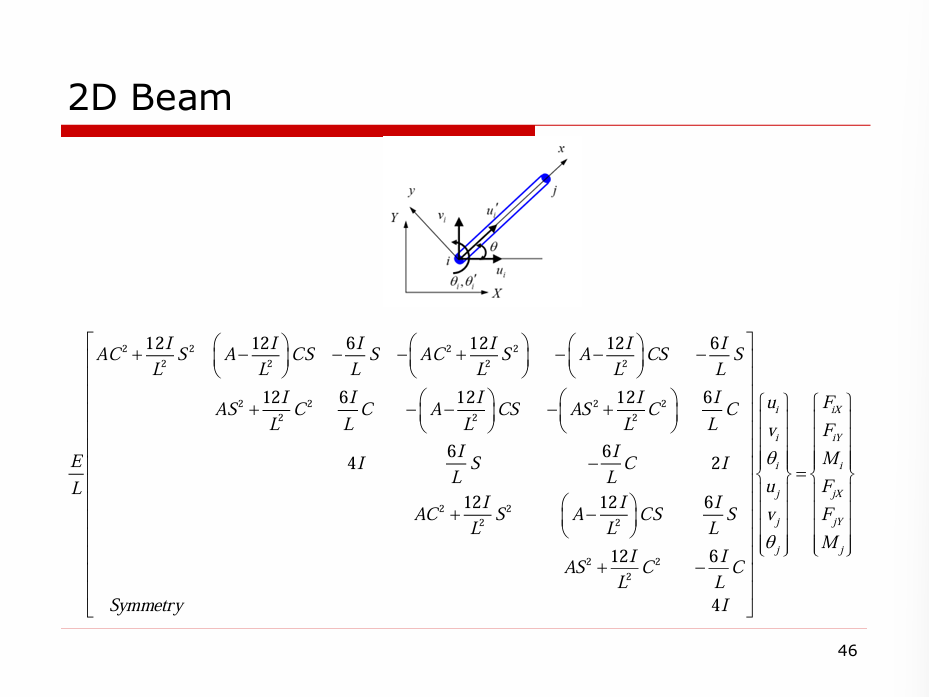
三维情况：
\[
u_{i} = \begin{bmatrix}
u_{i} & v_{i} & w_{i} & \theta_{ix} & \theta_{iy} & \theta_{iz}
\end{bmatrix}^{T}
\]
三维情况需要考虑扭转的作用；同样的，我们定义根据右手法则指向正方向为正。
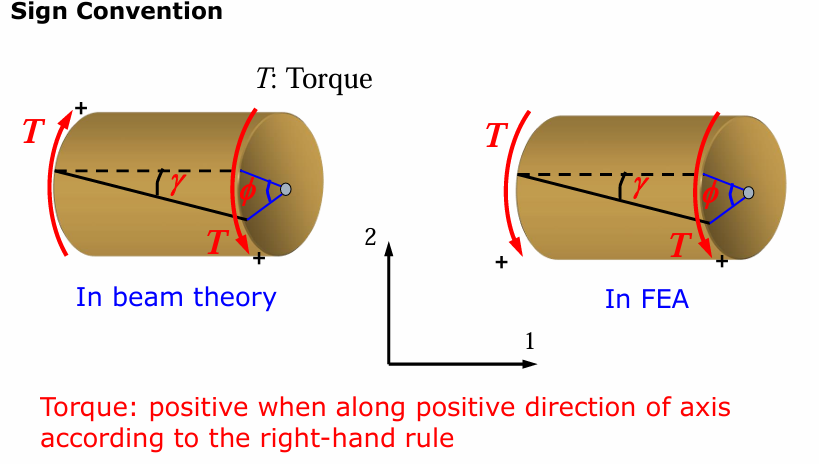
扭转对应的刚度矩阵： $$ \frac{GJ}{L}\begin{bmatrix} 1 & -1 \ -1 & 1 \end{bmatrix} $$ 其中 \(G\) 为剪切模量，\(J\) 为极惯性矩
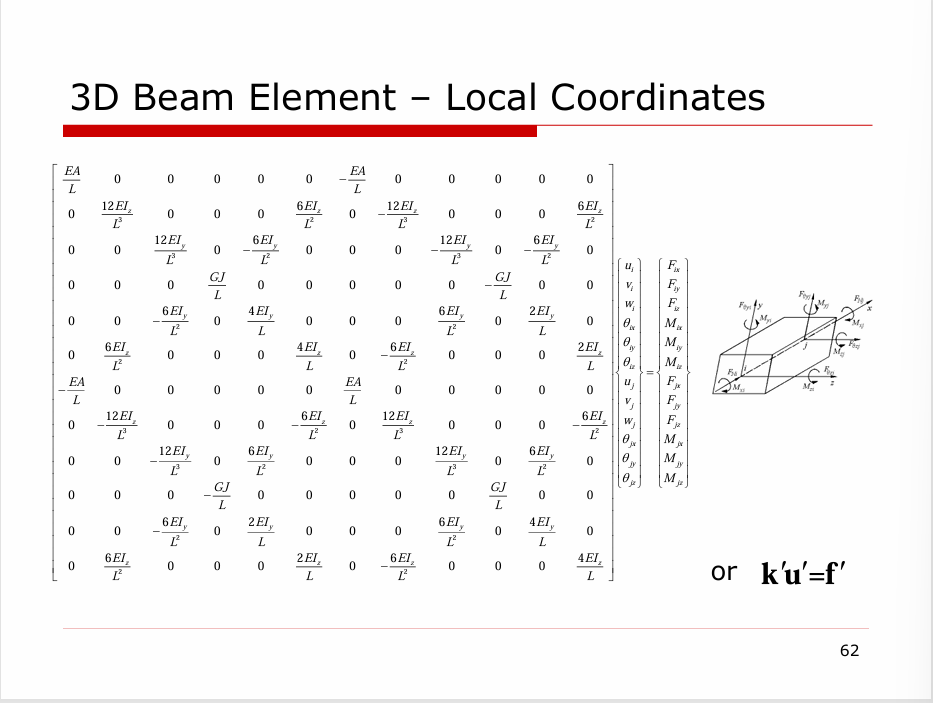
Plate
板可以视作梁的二维扩展形式。
- 只能承受法向载荷（transverse loading）
- 初始状态是平的（非平的板称为壳(shell)）
- 板可以抵抗两个轴方向的弯曲和扭转
基本假设：
- 厚度远小于板的长度或宽度(否则需要考虑切应力的作用)
- 挠度远小于厚度(否则需要考虑板内的屈曲作用，对于 von Karman 板)
基尔霍夫假设(Kirchhoff assumptions) ： （PS:来自弹性力学）
- 变形前垂直于薄板中面的直线段（法线），在薄板变形后仍保持为直线，且垂直于弯曲变形后的中面，其长度不变。如果我们选取薄板中面作为 \(Oxy\) 坐标平面，则有 \(\gamma_{xz}=0,\gamma_{yz} =0,\varepsilon_{z} = 0\)
- 与其他应力分量相比，垂直于中面的正应力 \(\sigma_{z}\) 和指向 \(z\) 轴的切应力 \(\tau_{xz},\tau_{yz}\) 很小，在计算应变时可略去不计。
- 薄板弯曲变形时，中面内各点只有垂直位移 \(w\) ,而无 \(x\) 方向和 \(y\) 方向的位移，因此中面应变分量 \(\varepsilon_{x},\varepsilon_{y},\gamma_{xy}\) 均等于零，即中面无应变发生，称中面内位移函数 \(w(x,y)\) 称为挠度函数
根据基尔霍夫假设给出
- 位移场：
\[
\begin{align} \\
&u = -z\frac{\partial w }{\partial x }
&v =-z\frac{\partial w }{\partial y }
\end{align}
\]
- 应变场：
\[
\varepsilon_{x}= - \frac{\partial^{2}w }{\partial x^{2} } z =-z \kappa_{x} \quad
\varepsilon_{y} = - \frac{\partial^{2} w}{\partial y^{2} }z = -z \kappa_{y} \quad
\gamma_{xy}= -2 \frac{\partial^{2}w }{\partial x \partial y } z =-z \kappa_{xy}
\]
- 应力场：
\[
\begin{align}
&\sigma _{x} = \frac{E}{1-\nu^{2}}(\varepsilon_{x}+\nu \varepsilon_{y}) \\
&\sigma_{y} = \frac{E}{1-\nu^{2}}(\varepsilon_{y}+\nu \varepsilon_{x}) \\
&\tau_{xy}=G\gamma_{xy}
\end{align}
\]
- 弯矩：
\[
M_{x}=D(\kappa_{x}+\nu \kappa_{y}) \quad M_{y} = D(\kappa_{y}+\nu \kappa_{x}) \quad M_{xy} =\frac{D(1-\nu)}{2}\kappa_{xy}
\]
其中
\[
D = \frac{Et^{3}}{12(1-\nu^{2})}
\]
称为抗弯刚度。
板满足的物理方程为：
\[
D \left( \frac{\partial^{4}w }{\partial x^{4} } + \frac{2\partial^{4}w }{\partial x^{2}\partial y^{2} } +\frac{\partial^{4}w }{\partial y^{4} } \right) = q
\]
- 应变能：
\[
U = \frac{1}{2}\int(M_{x}\kappa_{x}+M_{y}\kappa_{y}+M_{xy}\kappa_{xy})\mathrm{d}A
\]
对于一个节点，其节点位移矩阵
\[
\left\{ d_{i} \right\} = \begin{Bmatrix}
w_{i} \\
\theta_{xi} \\
\theta_{yi}
\end{Bmatrix}
\]
每个节点有三个自由度，对于一个板单元，我们有 \(12\) 个自由度，定义：
\[
\theta_{x} = + \frac{\partial w }{\partial y } \quad \theta_{y} = - \frac{\partial w }{\partial x }
\]
- 总单位位移矩阵：
\[
\left\{ d \right\} = \left\{ [d_{i}] \quad [d_{j}]\quad [d_{m}]\quad[d_{n}] \right\} ^{T}
\]
- 位移插值函数：
\[\begin{align}
w =& a_{1} +a_{2}x + a_{3} y+a_{4}x^{2}+a_{5}xy+a_{6} y^{2}+a_{7}x^{3}+a_{8}x^{2}y \\
&+a_{9}xy^{2}+a_{10}y^{3}+a_{11}x^{3}y +a_{12}xy^{3}
\end{align}
\]
将位移插值函数带入到节点位移矩阵可得系数方程，给出矩阵形式：
\[
\left\{ \psi \right\} = [P] \left\{ a \right\}
\]
为每一个节点计算如上方程，整合可得：
\[
\left\{ d \right\} = [C]\left\{ a \right\} \implies \left\{ a \right\} =[C]^{-1}\{d\}
\]
联系之前的系数方程有：
\[
\left\{ \psi \right\} = [P]\left\{ a \right\} \implies \left\{ \psi \right\} = [P][C]^{-1}\left\{ d \right\}
\]
定义形函数
\[
[N]= [P][C]^{-1}
\]
定义曲率矩阵：
\[
\left\{ \kappa \right\} = \begin{Bmatrix}
\kappa_{x} \\
\kappa_{y} \\
\kappa_{xy}
\end{Bmatrix}= \begin{Bmatrix}
-2a_{4}-6a_{7}x-2a_{8}y-6a_{11}xy \\
-2a_{6}-2a_{9}x-6a_{10}y-6a_{12}xy \\
-2a_{5}-4a_{8}x-4a_{9}-6a_{11}x^{2}-6a_{12}y^{2}
\end{Bmatrix}=[Q]\left\{ a \right\}
\]
由于 \(\left\{ a \right\} = [C]^{-1}\left\{ d \right\}\)，则曲率矩阵
\[
\left\{ \kappa \right\} =[Q]\left\{ a \right\} = [Q][C]^{-1}\left\{d \right\} = [B]\left\{ d \right\}
\]
其中 \([B]\) 称为梯度矩阵。
可以导出弯矩方程：
\[
\left\{ M \right\} = \begin{Bmatrix}
M_{x} \\
M_{y} \\
M_{xy}
\end{Bmatrix} = [D]\begin{Bmatrix}
\kappa_{x} \\
\kappa_{y} \\
\kappa_{xy}
\end{Bmatrix} = [D][B]\left\{ d \right\}
\]
其中 \([D]\) 是本构矩阵，对于各向同性材料，满足：
\[
[D] = \frac{Et^{3}}{12(1-\nu^{2})}\begin{bmatrix}
1 & \nu & 0 \\
\nu & 1 & 0 \\
0 & 0 & \frac{1-\nu}{2}
\end{bmatrix}
\]
刚度矩阵有如下形式给出：
\[
[k] = \iint[B]^{T}[D][B]\mathrm{d}x\mathrm{d}y
\]
分布载荷产生的表面力矩阵：
\[
\left\{ F_{s} \right\} = \iint[N_{s}]^{T}q \mathrm{d}x\mathrm{d}y
\]
对于在大小在 \(2b\times2c\) 的单元表面上作用均匀荷载 \(q\) 产生的力和力矩：
\[
\begin{Bmatrix}
f_{wi} \\
f_{\theta x i} \\
f_{\theta yi}
\end{Bmatrix} = 4cbq \begin{Bmatrix}
\frac{1}{4} \\
-\frac{c}{12} \\
\frac{b}{12}
\end{Bmatrix}
\]
组装可得全局矩阵