非线性振动
约 2451 个字 2 张图片 预计阅读时间 16 分钟
保守系统的非线性振动
根据能量守恒原理,保守系统的总能总是保持不变的,即
\[
\frac{1}{2} m \dot{x}^{2}+U(x) =E
\]
\(U(x)\) 为系统势能, \(E\) 满足一定非线性条件。可以得出
\[
\frac{dx}{\pm \sqrt{ \frac{2(E-U(x))}{m} }} = dt
\]
假定系统满足一定的周期性,且有一定的对称性。我们可以解出周期满足
\[
4 \int_{0}^{x_\max} \frac{dx}{ \sqrt{ \frac{2(E-U(x))}{m} }} = T
\]
对于简单的非线性恢复力 \(F(x) = x,x^{3},\dots x^{2n+1}\) 我们可以求出对应的解析解
如果恢复力中包含偶函数,例如 \(F(x) = k_{1}x +k_{2}x^{2}\) ,那么对应的势能为 \(U(x) = \frac{1}{2}k_{1}x^{2}+\frac{k_{2}}{3}x^{3}\) 。势能函数大概如图所示
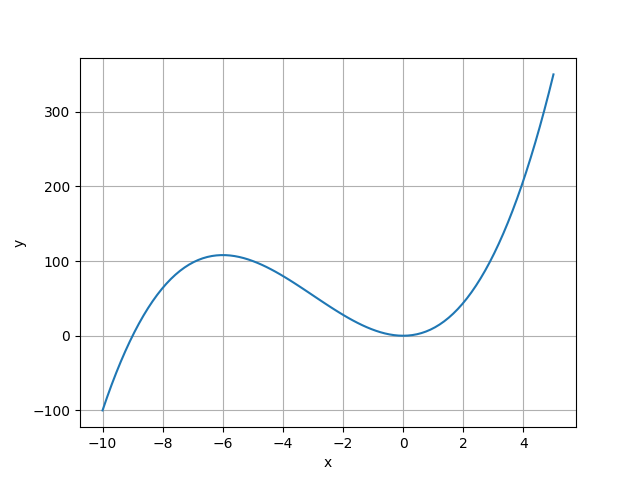
因为势能不能为零,为了保证其在 \(x\) 负半轴处有解。所以负半轴的势能取值限制了系统运动。取负半轴处最大值为 \(E_{\max}\)。所以总能量应满足关系式
\[
0< E <E_{\max}
\]
此时我们无法利用对称性求解周期,但在系统运动中,无论是从位移最大处 \(x_{\max}\) 到位移最小处 \(x_{\min}\) ,还是从位移最小处到位移最大处,两者的时间应当是相同的,因此
\[
T = 2 \int_{x_{\min}}^{x_{max}} \frac{{\, {\rm d}x }}{\sqrt{ \frac{2(E-U(x))}{m} }}
\]
非线性振动
对于非线性振动系统,将方程成线性部分和非线性部分
\[
\ddot{x} + \omega^{2} x = \varepsilon f(x,\dot{x})
\]
因为非线性部分源自刚度和阻尼;非线性振动中有两个比较典型的物理模型,分别对应不同的非线性项。
\[
\ddot{x} + 2c \dot{x} +k_{1}x+k_{3}x^{3} = f(t)
\]
\[
\ddot{x} +(c_0+c_1x^2+c_2\dot{x}^2)\dot{x} + kx = f(t)
\]
对于一般的非线性振动系统,我们很难给出准确的解析解,如果满足 \(0< \varepsilon\ll 1\) 也就是弱非线性情况,我们能给出近似解;对于强非线性情况,我们只有数值解。
平均摄动法
对于微分方程
\[
\ddot{x} +\omega^{2}x = \varepsilon f(x,\dot{x})
\]
由于 \(\varepsilon\) 是小参数,我们可以将解按 \(\varepsilon\) 直接展开的幂级数形式,即
\[
x(t,\varepsilon) =x_{0}(t)+\varepsilon x_{1}(t) +\varepsilon^{2} x_{2}(t)+\dots
\]
这里取非线性项为三次刚度 \(f(x) = x^{3}\) 我们将这个解带入我们的方程,一一比较系数显然可得
\[
\begin{align}
&\varepsilon^{0} : \ddot{x}_{0}+\omega^{2} x_{0} = 0 \\
&\varepsilon^{1} : \ddot{x}_{1} + \omega^{2} x_{1}=f(x_{0},\dot{x}_{0})\\
&\dots
\end{align}
\]
此时初始条件为
\[
x(0) = A \quad \dot{x}(0) = 0
\]
所以第一个方程给出解
\[
x_{0} = A \cos \omega t
\]
显然这是一个无外加激励时,保守系统的解。我们将这个解带入第二个方程
\[
\ddot{x}_{1} +\omega^{2} x =-\alpha A^{3} \cos ^{3}\omega t
\]
杜哈梅积分给出解的形式
\[
x_{1}(t) = C_{1} \cos \omega t +C_{2} \sin \omega t +\beta t \cos \omega t + \Gamma \cos \omega t
\]
\(C_{1},C_{2},\beta,\Gamma\) 为系数。注意第三项为一个含有 \(t\) 的长期项。尽管在一定时间内,方程的解具有的渐进性,但是随着时间的增加显然会出现发散解的现象。
L-P 法
引入新的时间变量
\[
\tau = \omega t
\]
其中 \(\omega\) 是关于 \(\varepsilon\) 的未知函数,满足
\[
\omega = \omega_{0} + \omega_{1}\varepsilon + \omega_{2}\varepsilon^{2}+\dots
\]
于是方程变为
\[
\omega^{2} x'' + \omega_{0}^{2}x = \varepsilon f\left( x(\tau),\omega \frac{{\rm{d}} x }{{\rm {d}} \tau } \right)
\]
我们依旧考虑三次刚度项,所以基本摄动法给出
\[
\begin{align}
&\varepsilon^{0} : \omega _{0}^{2}x''_{0}+\omega_{0}^{2} x_{0} = 0 \\
&\varepsilon^{1} :\omega_{0}^{2}x_{1}'' +2 \omega_{0} wx_{0}''+\omega_{0} ^{2} x_{1}= -x_{0}^{3} \\
&\dots
\end{align}
\]
初始条件仍相同,所以给出第一个方程的解
\[
x_{0} = A \cos \tau
\]
将上述解带入第二个方程可得
\[
\omega_{0}^{2} x_{1}''+\omega_{0}^{2}x_{1} = \frac{1}{4} \omega_{0}A_{0}\left( 8 \omega_{1}-\frac{3}{\omega_{0}} A_{0}^{2} \right) \cos \tau - \frac{1}{4} A_{0}^{3} \omega_{0}^{2}\cos 3 \tau
\]
右端第一项将引起共振从而出现长期项,为了使得长期项不出现,需令其系数为零,因此有
\[
\omega_{1} = \frac{3A^{2}}{8\omega_{0}}
\]
同样的可以求得剩下的 \(\omega_{i}\) 所以时间变量满足
\[
\tau = \omega t = \left( \omega_{0} + \frac{3A^{2}}{8\omega_{0}} \varepsilon+\dots\right) t
\]
如果我们取的级数项够多,有效的区域也就会又大
平均法(K-B 法)
\[
\ddot{x} +\omega_{0}^{2}x = \varepsilon f(x,\dot{x})
\]
对于上述方程,我们做如下假定
\[
\begin{align}
&\varepsilon = 0:\cases{x(t) = A \cos (\omega_{0}t+\varphi_{0})\\
\dot{x}(t) = -\omega_{0} A \sin(\omega_{0}t+\varphi_{0})} \\
&\varepsilon \neq {0}:
\cases{x(t) = a(t) \cos (\omega_{0}t+\varphi(t))\\
\dot{x}(t) = -\omega_{0} a(t) \sin(\omega_{0}t+\varphi(t))}
\end{align}
\]
此时补充条件
\[
\dot{a} \cos (\omega_{0}t+\varphi(t))-a \dot{\varphi}(t)\sin (\omega_{0}t+\varphi(t))=0
\]
将上述 \(\varepsilon\neq 0\) 的假设带入方程中 (考虑 \(\varepsilon=0 ,\varepsilon\neq 0\) ) 可得
\[
\begin{align}
&\dot{ a} = - \frac{\varepsilon}{\omega_{0}} f[ \quad] \sin (\omega_{0}t +\varphi) \\
& \dot{\varphi} = - \frac{\varepsilon}{\omega_{0}a} f[\quad] \cos (\omega_{0} t+\varphi )
\end{align}
\]
(PS:老师上课没写中间的东西那我不写也是合理的)
对于上述两项,等式的右边含有小量 \(\varepsilon\) 说明这两项也是一个小量,因此 \(a\) 和 \(\varphi\) 的变换过程是很缓慢的,也就是随 \(t\) 慢变的量,因此我们可以将其视作是一个平稳变化项和微小扰动的叠加。为了方便起见,我们记 \(\omega_{0}t +\varphi(t)\triangleq \psi\) 。那么右边就是一个关于变量 \(\psi\) 周期为 \(2\pi\) 的周期函数,那么我们总可以用三角函数展开,展开后我们只取一个近似项,便可以将上述转换为如下形式(具体细节参照季文美《机械振动》P516)
\[
\begin{align}
&\dot{ a} = - \frac{\varepsilon}{2 \pi\omega_{0}} \int_{0}^{2\pi} \sin \psi f(a \cos \psi,-\omega_{0}a\sin \psi) \, {\rm d} \psi \\
& \dot{\varphi} = - \frac{\varepsilon}{2\pi\omega_{0}a}\int_{0}^{2\pi} \cos \psi f(a\cos \psi,-\omega_{0} a \sin \psi) \, {\rm d} \psi
\end{align}
\]
因为这是一个慢变过程,所以在一个周期 \(t = \frac{2\pi}{\omega_{0}}\) 内可以将 \(a\) 和 \(\varphi\) 视作常数
Tip
例题源自季文美《机械振动》P518参数不重要,重要的是大概的解题过程(
求杜芬方程的周期解:
\[
\ddot{x} + \omega_{0}^{2}(x+\varepsilon x ^{3}) = 0
\]
当 \(\varepsilon = 0\) 时,方程有解
\[
\begin{align}
& x = a \cos \psi ,\quad \psi = \omega_{0} t +\theta \\
&\dot{x} = - \omega_{0}a \sin \psi
\end{align}
\]
当 \(\varepsilon \neq 0\) 时,我们仍然保留解的形式,但此时 \(a\) 和 \(\theta\) 都是时间 \(t\) 的函数。将解带入杜芬方程中可得
\[
\omega_{0} \dot{a} \sin \psi + \omega_{0} a \dot{\theta} \cos \psi= \varepsilon \omega^{2} a^{3} \cos ^{3} \psi
\]
补充方程
\[
\dot{a} \cos \psi = a \dot{\theta} \sin \psi
\]
将上述两个方程联立求解可得标准方程
\[
\begin{align}
& \dot{a} = \frac{1}{8} \varepsilon \omega_{0} a^{3} \left( 2 \sin 2 \psi + \sin 4 \psi \right) \\
& \dot{\theta} = \frac{1}{8} \varepsilon \omega_{0} a ^{2} \left( 3+ 4 \cos 2\psi + \cos 4 \psi \right)
\end{align}
\]
在 \(\frac{2\pi}{\omega_{0} }\) 时间内对时间项取平均
\[
\begin{align}
&\dot{ a} = 0 \\
& \dot{\theta} = \frac{3}{8} \varepsilon \omega_{0}a^{2}
\end{align}
\]
得到一次近似解
\[\begin{align}
&\overline{a}_{1} = a_{0} = \text{const} \\
&\overline{ \theta}_{1 }= \frac{3}{ 8} \varepsilon \omega_{0}a^{2} t + \theta_{0} \quad \psi_{1}=\omega_{0}\left( 1+ \frac{3}{8} \varepsilon a_{0}^{2} \right)t + \theta_{0}
\end{align}
\]
范德波方程
\[
\ddot{x} + \varepsilon(x^{2}-1) \dot{ x}+ x= 0
\]
同样取变换
\[
\begin{align}
& x = a \cos \psi ,\quad \psi = t +\theta \\
&\dot{x} = - a \sin \psi
\end{align}
\]
所以可得标准方程
\[
\begin{align}
&\dot{a} = \frac{1}{8}\varepsilon a [4-a ^{2}-4 \cos 2 \psi + a ^{2} \cos 4\psi] \\
&\dot{\theta} =\frac{1}{8}\varepsilon [(4-2a^{2})\sin 2 \psi - a ^{2} \sin 4 \psi]
\end{align}
\]
做平均化可得平均方程:
\[\begin{align}
&\dot{ a} = \frac{1}{ 8}\varepsilon a (4- a ^{2}) \\
&\theta = 0
\end{align}
\]
积分得
\[
\overline{a}^{2}_{1} = \frac{4}{1+\left( \frac{4}{a_{0}^{2}}-1 \right)e^{-\varepsilon t} } \quad \overline{\theta}_{1} = \theta_{0}
\]
极限环
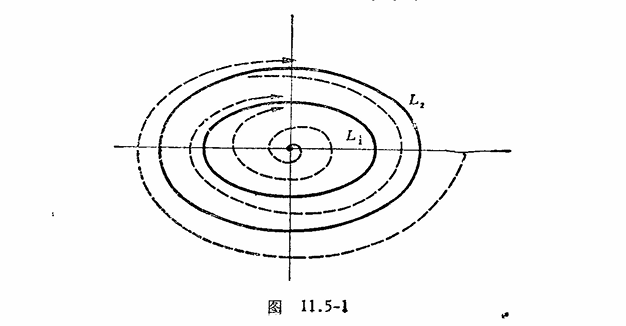
对于一个 VanderPol 振子我们所考虑的非线性阻尼是一个正的阻尼,而线性阻尼是一个负的阻尼。此时相平面上会出现一个闭轨线(图中L1)当初始时刻在闭轨线内部时,阻尼整体表现出负阻尼特性,由于负阻尼使得振荡系统发散,所以振幅逐渐变大,但是负阻尼特性会随振幅变大而减小,逐渐趋近闭轨线;同理,当初始时刻在闭轨线外部是,阻尼整体表现出正阻尼特性;正阻尼特性使得振荡系统衰减,但是正阻尼特性也随之减弱,所以也表现出逐渐趋近闭轨线,这样的闭轨线成为极限环。
如果极限环的两侧相轨线都逐渐趋于它,则极限环是稳定的。如果哪怕有一侧的相轨迹是离开它的,极限环是不稳定的。稳定的极限环对应于系统的稳态周期运动,这样的稳态运动称为自激振动或者简称自振。自振发生于系统受到某些不可避免的干扰而自发地开始振动,振幅一直增长至系统的非线性因素起作用而限制振幅为止。这种运动之所以能够维持,是由于存在一个系统有关的外部恒定能源,又由于系统固有的非线性机制,在运动着的系统与恒定能源之间引起交变力的出现,使系统周期性地从恒定能源获取能量,平衡由于阻尼而造成地能量损耗。

