Convolutional Networks

约 2864 个字 8 张图片 预计阅读时间 19 分钟

Components of a Convolutional Network

• Fully-Connected Layers
• Convolution Layers
• Activation Function
• Pooling Layers
• Normalization

Fully-Connected Layers

在全连接层中，神经元对于前一层中的所有激活数据是全部连接的，这个常规神经网络中一样。它们的激活可以先用矩阵乘法，再加上偏差。

对于高维感知数据，单纯的全连接层可能会变得不适用，假设我们有一个足够充分的照片数据集，数据集中是拥有标注的照片，每张照片具有百万级像素，这意味着网络的每次输入都有一百万个维度。 即使将隐藏层维度降低到1000，这个全连接层也将有\(10^6\times10^3=10^9\)个参数。 想要训练这个模型将不可实现，因为需要有大量的GPU、分布式优化训练的经验和超乎常人的耐心。在真实的系统中我们仍然需要数十亿个参数。 此外，拟合如此多的参数还需要收集大量的数据。

Convolution Layers

卷积层是构建卷积神经网络的核心层，它产生了网络中大部分的计算量。

一次卷积操作：

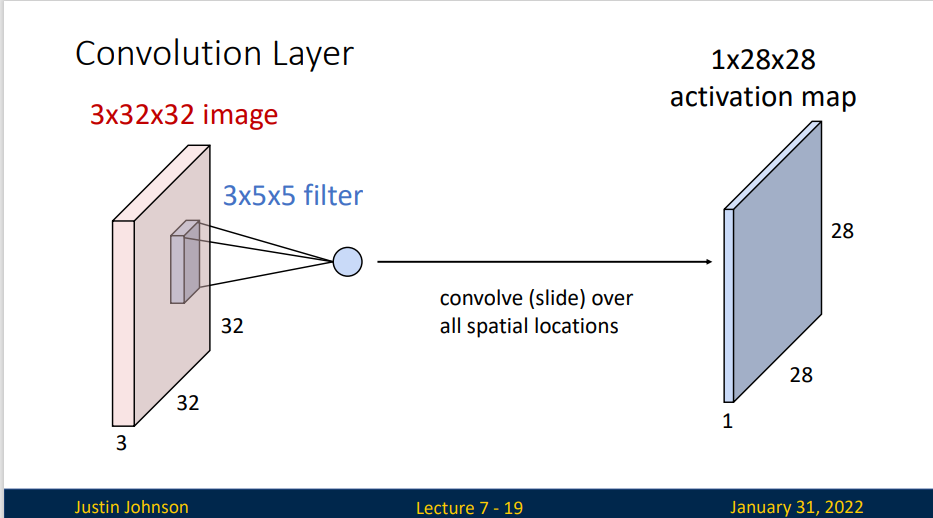
我们使用一个卷积核或过滤器，进行卷积操作，并且将输出结果组成一个特征图，这个过程是线性的，一个核就是一个模板，输出结果就是这块图像与模版的匹配程度

比如，我们选择了一个 \(3\times 5\times 5\) 过滤器，对图像数据操作后得到了一个\(1\times 28\times 28\)的激活映射图（activation map）（过滤器需要选取图像中的有效数据，我们并没有设置额外的边界条件，所以输出的结果的大小会减少） spatial dimensions: Input：W Filter：K Output：W-K+1

Filters always extend the full depth of the input volume.

事实上，一个卷积核往往是不够的，因此我们会选取多个卷积核，并且以多维张量形式表示.

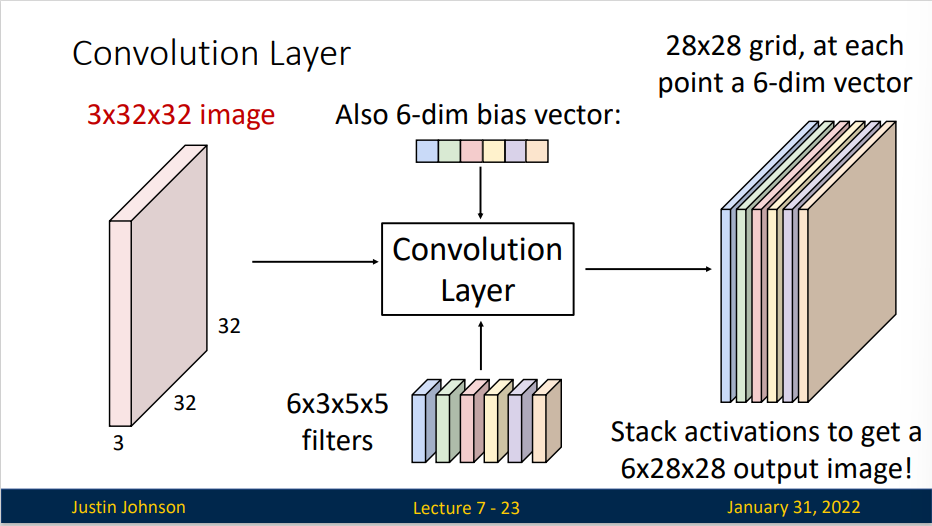
一个卷积层结构类似于上图，有六个卷积核，所以卷积核为一个四维张量，每个卷积核大小为 \(3\times5\times 5\)。于是一个 \(3\times32\times32\)的图片，经过大小为\(6\times 3\times5\times5\)的卷积核卷积，并加上一个6维的偏差向量（bias vector）得到六张特征图 \(6\times 28\times 28\)

但是单纯的多次卷积操作并不能得到更好的结果，因为实际上卷积是线性操作，多个卷积仍是线性网络，所以我们还需要加上激活函数，这样才能更好的学习。

3个超参数控制着输出数据体的尺寸：深度（depth），步长（stride）和零填充（zero-padding）。下面是对它们的讨论：

1. 首先，输出数据体的深度是一个超参数：它和使用的滤波器的数量一致，而每个滤波器在输入数据中寻找一些不同的东西。举例来说，如果第一个卷积层的输入是原始图像，那么在深度维度上的不同神经元将可能被不同方向的边界，或者是颜色斑点激活。我们将这些沿着深度方向排列、感受野相同的神经元集合称为深度列（depth column），也有人使用纤维（fiber）来称呼它们。
2. 其次，在滑动滤波器的时候，必须指定步长。当步长为1，滤波器每次移动1个像素。当步长为2（或者不常用的3，或者更多，这些在实际中很少使用），滤波器滑动时每次移动2个像素。这个操作会让输出数据体在空间上变小。
3. 有时候将输入数据体用0在边缘处进行填充是很方便的。这个零填充（zero-padding） 的尺寸是一个超参数。零填充有一个良好性质，即可以控制输出数据体的空间尺寸（最常用的是用来保持输入数据体在空间上的尺寸，这样输入和输出的宽高都相等）。

输出数据体在空间上的尺寸可以通过输入数据体尺寸（W），卷积层中神经元的感受野尺寸（F），步长（S）和零填充的数量（P）的函数来计算。

对于零填充，一般取零填充的值\(P=(F-1)/2\)，这样就能保证输入核输出数据体有相同的空间尺寸。输出数据体的空间尺寸为\((W-F +2P)/S+1\)。

步长的限制：这些空间排列的超参数之间是相互限制的。这些超参数会影响着输出数据体的空间尺寸大小，而当其值不为整数时，也就是说神经元不能整齐对称地滑过输入数据体，这些超参数地设定就被认为是无效的。于是，这些超参数的设定就被认为是无效的，一个卷积神经网络库可能会报出一个错误，或者修改零填充值来让设置合理，或者修改输入数据体尺寸来让设置合理，或者其他什么措施。

• Receptive Fields
  • For convolution with kernel size \(K\), each element in the output depends on a \(K\times K\) receptive field in the input.
  • Each successive convolution adds \(K-1\) to the receptive field size With \(L\) layers the receptive field size is \(1+L*(K-1)\)

在处理图像这样的高维度输入时，让每个神经元都与前一层中的所有神经元进行全连接是不现实的。相反，我们让每个神经元只与输入数据的一个局部区域连接。该连接的空间大小叫做神经元的感受野（receptive field），它的尺寸是一个超参数（其实就是滤波器的空间尺寸）。在深度方向上，这个连接的大小总是和输入量的深度相等。需要再次强调的是，我们对待空间维度（宽和高）与深度维度是不同的：连接在空间（宽高）上是局部的，但是在深度上总是和输入数据的深度一致。

Pooling Layers

Another way to downsample

Hyperparameters:

• Kernel Size
• Stride
• Pooling function

通常，在连续的卷积层之间会周期性地插入一个汇聚层。它的作用是逐渐降低数据体的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合。汇聚层使用MAX操作，对输入数据体的每一个深度切片独立进行操作，改变它的空间尺寸。最常见的形式是汇聚层使用尺寸2x2的滤波器，以步长为2来对每个深度切片进行降采样，将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值（也就是在深度切片中某个2x2的区域）。深度保持不变。

在实践中，最大汇聚层通常只有两种形式：一种是 \(F=3,S=2\) 也叫重叠汇聚（overlapping pooling），另一个更常用的是 \(F =2,S =2\) 。对更大感受野进行汇聚需要的汇聚尺寸也更大，而且往往对网络有破坏性。

普通汇聚（General Pooling）：除了最大汇聚，汇聚单元还可以使用其他的函数，比如平均汇聚（average pooling）或L-2范式汇聚（L2-norm pooling）。平均汇聚历史上比较常用，但是现在已经很少使用了。因为实践证明，最大汇聚的效果比平均汇聚要好。

不使用汇聚层：很多人不喜欢汇聚操作，认为可以不使用它。比如在Striving for Simplicity: The All Convolutional Net一文中，提出使用一种只有重复的卷积层组成的结构，抛弃汇聚层。通过在卷积层中使用更大的步长来降低数据体的尺寸。有发现认为，在训练一个良好的生成模型时，弃用汇聚层也是很重要的。比如变化自编码器（VAEs：variational autoencoders）和生成性对抗网络（GANs：generative adversarial networks）。现在看起来，未来的卷积网络结构中，无汇聚层的结构不太可能扮演重要的角色。

Batch Normalization

"Normalize" the outputs of a layer so they have zero mean and unit variance

We can normalize a batch of activations like this:

\[ \hat{x }= \frac{x-E[x]}{\sqrt{Var [x]}} \]

This is a differentiable function, so we can use it as an operator in our networks and backprop through it.

训练神经网络出现问题：

1. 数据预处理的方式会对最终结果产生巨大影响。
2. 对于典型的多层感知机或卷积神经网络，当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型参数的随着训练更新变幻莫测。
3. 更深层的网络很复杂，容易过拟合。

批量规范化（Batch Normalization）可应用于单个可选层，其原理如下：在每次训练迭代中，我们首先规范化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。 接下来，我们应用比例系数和比例偏移。

请注意，如果我们尝试使用大小为1的小批量应用批量规范化，我们将无法学到任何东西。 这是因为在减去均值之后，每个隐藏单元将为0。 所以，只有使用足够大的小批量，批量规范化这种方法才是有效且稳定的。 请注意，在应用批量规范化时，批量大小的选择可能比没有批量规范化时更重要。

批量规范化表达式：

\[ y_{i,j}= \gamma_j\hat{x}_{i,j}+\beta_j \]

其中 \(\gamma\) 称为拉伸参数， \(\beta\) 称为偏移参数，是需要与其他模型参数一起学习的参数

Per-channel mean, shape is D

\[ \mu_j= \frac{1}{N}\sum^{N}_{i=1}x_{ij} \]

Per-channel std, shape is D

\[ \sigma^2_j = \frac{1}{N}\sum^{N}_{i=1}(x_{i,j}-\mu_j)^2 \]

有些时候会在方差估计值中添加一个小的常量 \(\varepsilon>0\)，以确保我们永远不会尝试除以零，即使在经验方差估计值可能消失的情况下也是如此。

Normalized x, Shape is N x D

\[ \hat{x}_{i,j}=\frac{x_{i,j}-\mu_j}{\sqrt{\sigma^2_j+\varepsilon}} \]

Problem: Esitmates depend on minibatch; can't do this at test-time

\[ \begin{align} &\mu_j = \text{(Running) average of values seen during training}\\ &\sigma^2_j = \text{(Running) average of values seen during training} \end{align} \]

That is

\[ \begin{align} &\mu_i^{test} = 0\\ &\text{For each training iteration:}\\ &\qquad \mu_j= \frac{1}{N}\sum^{N}_{i=1} x_{i,j}\\ &\qquad \mu_j^{test} = 0.99 \mu_j^{test}+0.01\mu_j \end{align} \]

(Similar for \(\sigma\)) During testing batchnorm becomes a linear operator! Can be fused with the previous fully-connected or cov layer

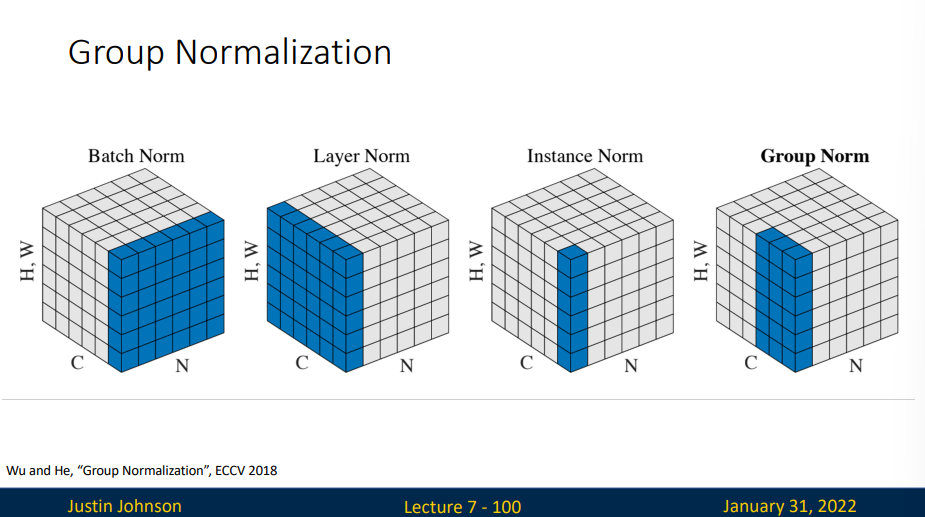
Convolutional Networks

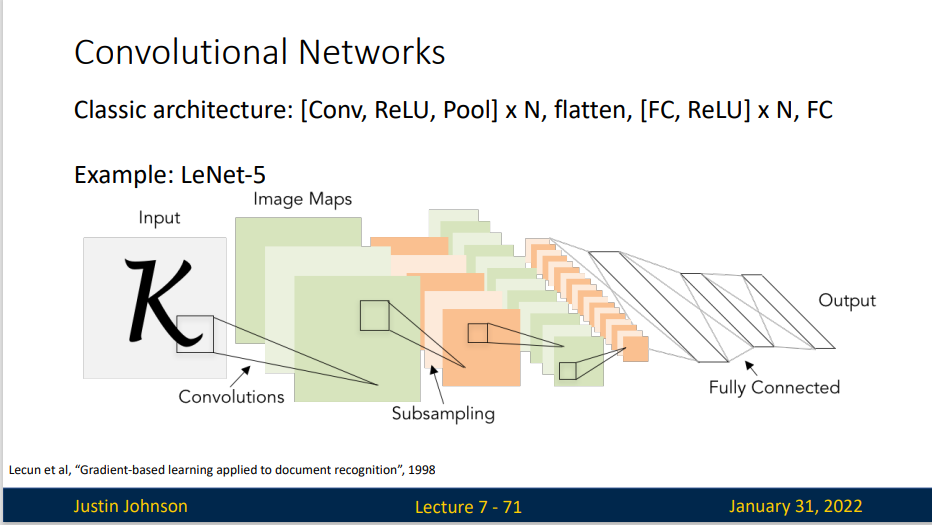
卷积神经网络最常见的形式就是将一些卷积层和ReLU层放在一起，其后紧跟汇聚层，然后重复如此直到图像在空间上被缩小到一个足够小的尺寸，在某个地方过渡成成全连接层也较为常见。最后的全连接层得到输出，比如分类评分等

As we go through the network: Spatial size decreases (using pooling or strided conv) Number of channels increases (total “volume” is preserved!) Some modern architectures break this trend -- stay tuned!