Linear System

约 1372 个字 2 张图片 预计阅读时间 9 分钟

Linear Systems

简单的线性控制系统可以为描述为：

\[ \dot{x} = Ax +Bu \]

其中 \(Bu\) 表示我们的控制。当不考虑控制影响时，即考虑 \(\dot{x} =Ax\) 对应解：

\[ x(t) = e^{At}x(0) \]

\(A\) 是一个矩阵，我们可以利用如下泰勒展开计算结果：

\[ e^{At} = I+At +\frac{A^{2}t^{2}}{2} +\frac{A^{3} t^{3}}{3!} + \dots \]

---

考虑一个如下坐标变换

\[ x = T z \]

其中 \(T\) 是矩阵 \(A\) 对应的特征向量构成的矩阵，满足 \(A = TDT^{-1}\) ，\(z\) 是特征向量方向上的坐标。

\[ \begin{align} \dot{x} = T \dot{z} & = Ax \\ T\dot{z} & = ATz \\ \dot{z} &= T^{-1}ATz \\ \dot{z} &= Dz \end{align} \]

此时我们将原本动力学系统变换到了一个特殊 \(z\) 坐标系中，在这个坐标系中，系统的方程变成了一个简洁的对角形式，这也意味着各个分量之间相互解耦。带回到泰勒展开表达式：

\[ \begin{align} e^{TDT^{-1}t} &= TT^{-1} + TDT^{-1}t +\frac{TD^{2}T^{-1}}{2}t^{2}+\dots \\ &=T\left[ I+D+\frac{D^{2}t^{2}}{2!}+\dots \right]T^{-1} \\ &=T[e^{Dt}]T^{-1} \end{align} \]

所以

\[ x(t) = Te^{Dt}T^{-1}x(0) = Te^{Dt}z(0) = Tz(t) \]

所以我们分解线性系统中的特征值和特征向量，在这些特征向量坐标中，动力学系统变得很简单

Stability

接下来讨论系统的稳定性，也就是当时间趋于无穷大时，系统会呈现出怎样的行为，这与 \(e^{Dt}\) ，注意这时候 \(D\) 是对角特征矩阵：

\[ e^{Dt} = \begin{bmatrix} e^{\lambda_{1}t} & & &0 \\ & e^{\lambda_{2}t} & & \\ & & \ddots & \\ 0& & & e^{\lambda_{n}t} \end{bmatrix} \]

这些项中，即使其中只有一个趋向于无穷大也会导致 \(x\) 在某个方向趋向于无穷大，这并不是我们想要的事情。

考虑特征值 \(\lambda = a +\mathrm{i} b\) ，这里有点奇怪，因为我们在一个实值系统中考虑了复数，但是当我们考虑复数时，虚部总是以相反数的形式出现，即 \(\lambda = a\pm \mathrm{i} b\) ，从物理或数学的角度来说，当我们将混合项相加后，虚部会抵消，最终会得到实数的输出。

利用欧拉公式：

\[ e^{\lambda t} = e^{a t}\left[ \cos (bt) +\mathrm{i} \sin (bt) \right] \]

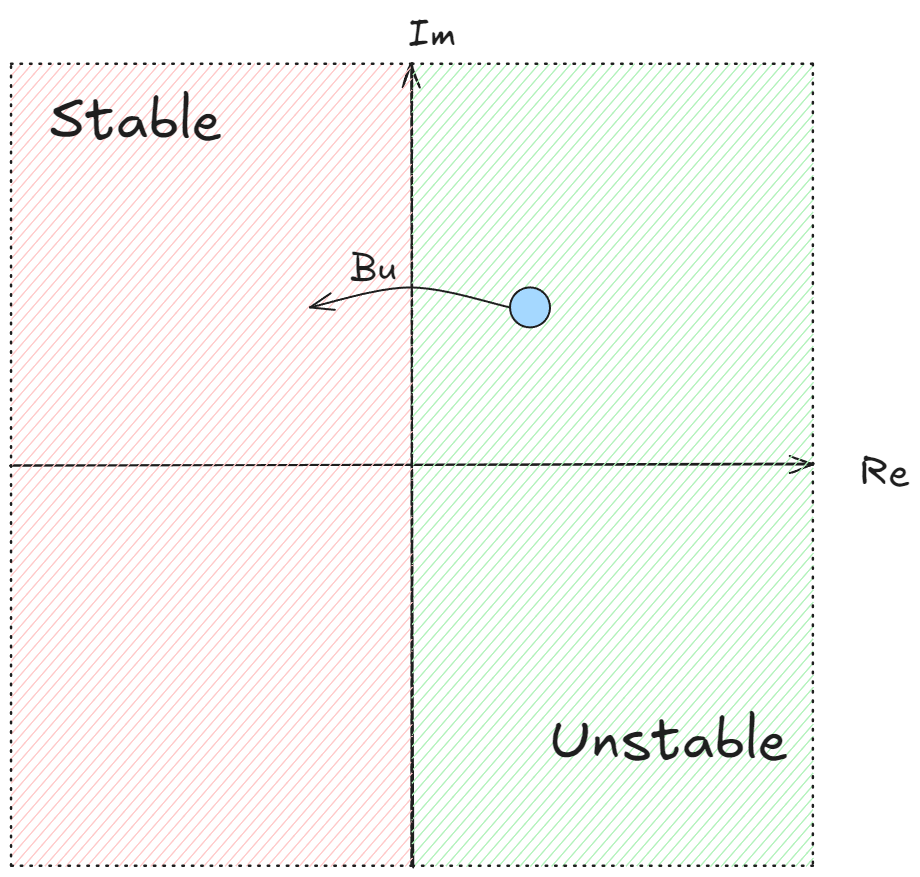
• 当 \(a > 0\) 系统以正弦波形式震荡，但是振幅以指数形式增大（指数增长的包络）
• 当 \(a < 0\) 系统以正弦波形式震荡，但是振幅以指数形式衰减（指数衰减的包络）

因此，当所有的特征值实部小于零时，系统是稳定的。在设计时，我们原本的线性系统的一部分特征值落在不稳定的区域，但是我们的驱动项 \(Bu\) 可以迫使其到达稳定区域

---

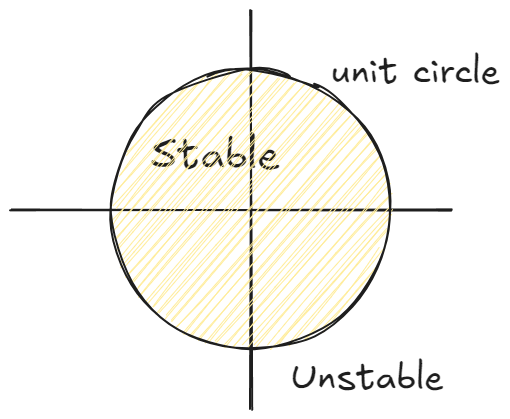
如果考虑一个离散系统

\[ X_{k+1} = \tilde{A}x_{k} ,x_{k} = x(k\Delta t) \]

\[ \tilde{A} = e^{ A\Delta t } \]

在离散时间中也存在稳定性的问题。我们将特征值以极坐标形式表示：\(\lambda = Re^{i\theta}\) 。对于第 N 时刻 \(x_{N}= \tilde{A}^{N}x_{0}\) ，对应的特征值为 \(\lambda^{N} = R^{N} e^{iN\theta}\) ，对应在复平面上半径要么增大要么减小，而角度发生不停的旋转。因此当半径大于 \(1\) 时，\(\lambda^{N}\) 会无穷增大，当半径小于 \(1\) 时， \(\lambda^{N}\) 会衰减到零。所以所有特征值必须位于单位圆内系统才能保持稳定。

Linearizing around a fixed point

考虑一个非线性系统：

\[ \dot{x} = f(x) \]

可以通过以下步骤获得一个线性系统：

• 先找到固定点 \(f(\bar{x}) = 0\)
• 在 \(\bar{x}\) 附近进行线性化，即计算 \(\left .\frac{{\rm{D}} f }{{\rm {D}} x }\right\vert_{\bar{x}} =\left[ \frac{\partial f_{i} }{\partial x_{j} } \right]\)

利用泰勒展开可以知道，在非线性系统的固定点附近系统的表现近似线性：

\[ \Delta \dot{x} = A\Delta x = \frac{{\rm{D}} f }{{\rm {D}} x }\Big|_{\bar{x}}\Delta x \]

如果我们的控制项 \(Bu\) 有效，我们能够使系统保持在该固定点附近，它能够稳定该系统并使其维持在固定点附近且表现良好。

但是线性化并不能总是准确描述非线性周围的动态特性。

Hartman-Grobman theorem

动力系统在双曲平衡点（特征值有非零实部）附近的域中的行为与其在该平衡点附近的线性化行为近似相同。因此，在处理此类动力系统时，可以使用系统的更简单的线性化来分析其围绕平衡的行为

但如果特征值是纯虚数的话，线性化会失效。

Example

考虑一个简单的摆系统：

\[ \ddot{\theta} = -\sin\theta -\delta \dot{\theta} \]

系统状态：

\[ \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}= \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix}\quad \frac{{\rm{d}} }{{\rm {d}} t }\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} x_{2} \\ -\sin(x_{1})-\delta x_{2} \end{bmatrix} \]

先寻找固定点

\[ \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \end{bmatrix}\quad\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}= \begin{bmatrix} \pi \\ 0 \end{bmatrix} \]

Jacobian 矩阵

\[ A =\begin{bmatrix} 0 & 1 \\ -\cos(x_{1}) & -\delta \end{bmatrix} \]

将固定点带入：

\[ A|_{\bar{x}=[0,0]} = \begin{bmatrix} 0 & 1 \\ -1& -\delta \end{bmatrix}\quad A|_{\bar{x}=[\pi,0]} = \begin{bmatrix} 0 & 1 \\ 1& -\delta \end{bmatrix} \]

可以求得在第二个固定点的 Jacobian 对应的特征值存在大于零的，换言之这是一个不稳定的定点，而 \([0,0]\) 是一个稳定的定点