Deep RL with Q-Functions

约 3330 个字 4 张图片 预计阅读时间 22 分钟

slides

online Q iteration 算法还有一个问题，当选取一次转移后采样，得到的样本和上一个样本有高度的相似性，将其带入计算梯度时会违反随机梯度的假设，而且效果不好。

总结一下，在线 Q 学习中主要有两个问题：

1. 相邻状态高度相关
2. 目标值总是在变化，这有点像追逐自己的尾巴。

回到行为克隆所讨论的一个问题：在模仿学习中考虑的是一个序列决策的问题，训练点之间是会相互影响的。在线 Q 学习所作的更像是在一段函数的局部做一个过拟合（因为样本之间高度相似），然后你获得了下一段的样本，然后再做过拟合，重复这些动作，当你开始新的动作以后，函数逼近器实际上停留在上一段的过拟合状态，因此导致效果不佳，显然，当我们同时对这些样本进行拟合的效果会比在一小段局部上过拟合的效果要好。

借鉴 Actor-Critic 的并行化算法，我们让多个工作者同时收集不同的样本，然后再这些样本上进行更新，原则上可以解决高度相关的问题，不过我们也并没有解决这个问题，只不过是缓解他。当然也有异步的方法，实际上，对于 Q 学习，这个方法理论上效果更好，这是因为在 Q 学习中，我们并不需要工作者使用最新的策略

Replay Buffer

Replay Buffer 就像在考试前，不是只复习刚刚学的新知识，而是反复温习以前学过的内容，让记忆更加巩固、泛化能力更强。

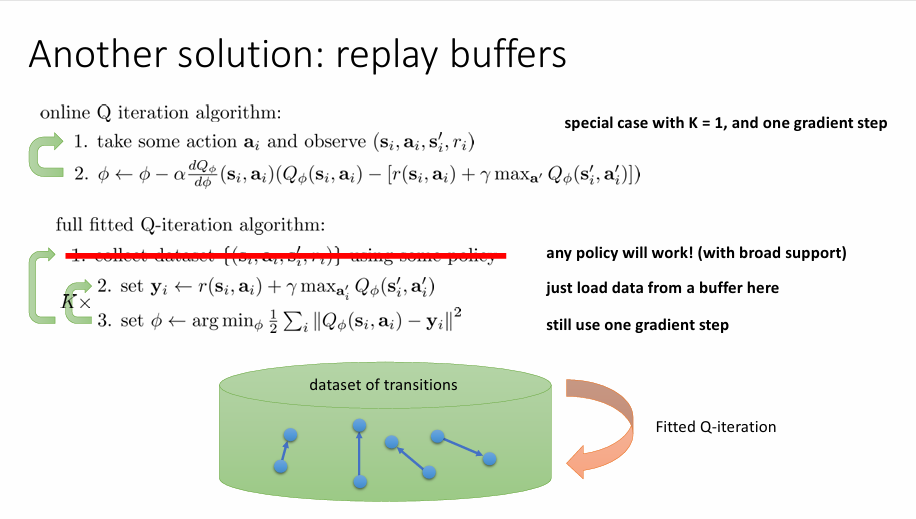
另一种方法是重放缓冲区（replay buffer）。在 full fitted Q-iteration 算法中，第一步是使用策略产生新的样本并收集，由于产生的样本有高度相似性，我们舍弃这个行为转而从从一个比较大的数据集中收集数据并用于训练，我们并不关心这些数据从哪里来，只要它能够掩盖数据之间的相关性。将这个思想运用到 Q 学习中有：

Q-learning with a replay buffer

1. Sample a batch \((\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}'_{i},r_{i})\) from \(\mathcal{B}\)
2. \(\phi \leftarrow \phi - \alpha \sum_{i}^{}\frac{{\rm{d}} Q_{\phi} }{{\rm {d}} \phi }(\mathbf{s}_{i},\mathbf{a}_{i})(Q_{\phi}(\mathbf{s}_{i},\mathbf{a}_{i})-[r(\mathbf{s}_{i},\mathbf{a}_{i})+\gamma\max_{\mathbf{a}'} Q_{\phi}(\mathbf{s}_{i}',\mathbf{a}_{i}')])\)

因此，我们从缓冲区 \(\mathcal{B}\) 中获取一批样本数据然后做梯度更新，在每次更新中，我们采取不同批次的样本，这些样本是从 \(\mathcal{B}\) 中采用独立同分布的方法来获取的，所以他们不具有相关性，其次，我们采用批量下降从而降低了方差。我们只需要定期地往缓冲池提供一些数据来掩盖原有糟糕策略产生的数据。

full fitted Q-iteration algorithm

1. 收集数据 \(\left\{ (\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}_{i}',r_{i}) \right\}\)，并更新数据集 \(\mathcal{B}\)
2. Sample a batch \((\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}'_{i},r_{i})\) from \(\mathcal{B}\)
3. \(\phi \leftarrow \phi - \alpha \sum_{i}^{}\frac{{\rm{d}} Q_{\phi} }{{\rm {d}} \phi }(\mathbf{s}_{i},\mathbf{a}_{i})(Q_{\phi}(\mathbf{s}_{i},\mathbf{a}_{i})-[r(\mathbf{s}_{i},\mathbf{a}_{i})+\gamma\max_{\mathbf{a}'} Q_{\phi}(\mathbf{s}_{i}',\mathbf{a}_{i}')])\)

重复 2 和 3 \(K\) 次

Target Networks

但是我们还是没有解决 Q 学习中目标函数不断变化的问题，这导致了我们的梯度下降并不是朝着目标值前进。在 Q 迭代算法中，第三步的操作非常类似于监督学习，本质上是对 \(\mathbf{y}_{i}\) 做一个回归，实际上，如果算法收敛的话，第三步收敛会收敛到目标值，尽管这个目标在不知情的情况下发生了变化，但这件事并不是一件好事。我们希望算法在某种程度上兼具完全拟合 Q 迭代算法中训练至收敛的稳定性但不并没有真的收敛。

一个解决办法是引入一个目标网络（Target Network），具体细节如上图所示，核心思想是让目标值计算使用一个延迟更新的网络，以避免训练过程中目标不稳定的问题。一个形象的比喻是像打靶练习，每次更新瞄准点容易导致一定程度的扰动，因此要把目标钉死一段时间才能看清误差并稳定优化。因此，先将参数固定住，然后重复原有的算法 N 次，此时目标值就不会发生变化，然后再更新参数。

classic deep Q-learning algorithm

1. take some action \(\mathbf{a}_{i}\) and observe \((\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}'_{i},r_{i})\) , add it to \(\mathcal{B}\)
2. sample mini-batch \(\left\{ \mathbf{s}_{j},\mathbf{a}_{j},\mathbf{s}'_{j},r_{j} \right\}\) from \(\mathcal{B}\) uniformly
3. compute \(y_i = r_{i}+\gamma \max_{\mathbf{a}'_{j}}Q_{\phi'}(\mathbf{s}',\mathbf{a}')\) using target network
4. \(\phi \leftarrow \phi - \alpha \sum_{j}^{}\frac{{\rm{d}} Q_{\phi} }{{\rm {d}} \phi }(\mathbf{s}_{i},\mathbf{a}_{i})(Q_{\phi}(\mathbf{s}_{i},\mathbf{a}_{i})-y_{j})\)
5. update \(\phi'\)

实际上，经典的 DQN 算法就是上面算法取 K=1 的特殊情况。为了避免参数的变化太过突兀，取如下更新方式：

\[ \phi' \leftarrow \tau \phi'+(1-\tau)\phi' \]

\(\tau\) 称为平滑参数，取 \(0.999\) 效果良好。

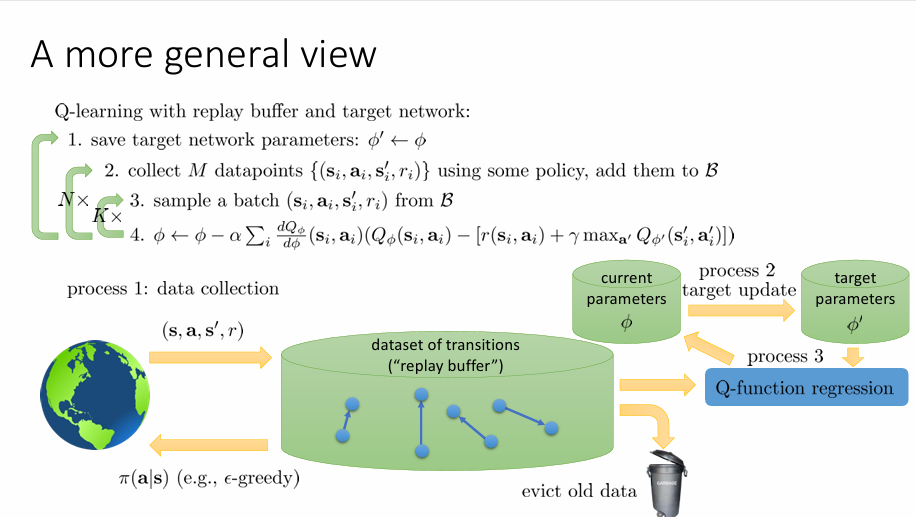
现在考虑将算法拆分成并行的过程。

过程一是收集数据的过程（Data collection），利用当前策略 \(\pi(\mathbf{a}|\mathbf{s})\) 与环境交互，生成 M 个 transition \((\mathbf{s},\mathbf{a},\mathbf{s}',r)\) ，将其放入缓冲池中 \(\mathcal{B}\) ，采用环形结构，也就是说，当缓冲池样本数据满了以后，当有新的数据添加进来时，舍弃最旧的数据。

过程二是更新网络参数的过程，也就是周期性地把当前网络参数同步到目标网络 \(\phi'\) 中

过程三是利用缓冲池中的数据做 Q 函数回归的过程。

Improving Q learning

现在考虑 Q 函数是否是准确的，尽管在学习过程中将 Q 函数视作是一个抽象对象，只考虑令其取极大的时候，但 Q 函数本身也一种预测，因而检测 Q 函数的预测准确性也是很重要的。

一般而言，随着训练的运行，我们的策略变得更好，获得了更高的奖励，因此 Q 函数也应当预测它会获得更高的 Q 值。考虑一个打砖块的游戏，当即将打到第一个砖块时，Q 函数会给出一个相对较高的值；但小球反弹时，Q 函数又会给出一个相对较低的值，提示小球反弹。如果遇到这样一个特殊情况：小球穿过了某一角，绕到了砖块的后方，那么此时小球会打掉更多的砖块，因此，当即将打出一个通道时，Q 函数会预测一个比较高的 Q 值，因为即将收获更多的分数，尽管打掉砖块后小球反弹，Q 值下降；当你绕到了砖块背后，Q 函数会给出一个特别高的值，而此后 Q 函数会逐渐下降，因为对砖块的收益在逐渐减小，或者说很难再遇到如此美妙的环节了。

考虑 Pong 这个游戏，当你的球离你很远的时候，Q 函数对所有动作预测的值可能会相同，假如将板上移是最优解，那么一个性能良好的 Q 函数会认为，即使这个时刻没有将板上移而做了其他动作，但是下一个时刻将板上移仍然能够收获一个很好的结果。

但是有一个问题，在一次成功的训练运行中，Q 函数的实际绝对值在实践中并不能用于预测真实值，这是因为 Q 函数给出的预测总是远远比真实值大。

考虑两个随机变量 \(X_{1}\) 和 \(X_{2}\) 并增加一点随机噪声（高斯白噪声），会有如下性质：

\[ \mathbb{E}[\max(X_{1},X_{2})]\geq \max(\mathbb{E}(X_{1}) ,\mathbb{E}(X_{2})) \]

这是因为尽管噪声的影响是零偏差的，但是在 \(\max(X_{1},X_{2})\) 选择过程中，我们倾向于选择受正噪声影响的随机变量，虽然存在负噪声，但其很少其作用，这导致我们的估计会偏大。 Q 函数并不是一个很完美的函数，他带有一定噪声，因此在 \(\max_{\mathbf{a}'}Q_{\phi'}(\mathbf{s}',\mathbf{a}')\) 的过程中会倾向于过度估计下一个值（放大噪声影响），这就导致了 Q 函数的预测远远比真实值大。

也就是说 \(Q_{\phi'}\) 由于噪声错误地认为某个动作更好，我们用于目标的值就是选择这个动作的值，他们带有相同的噪声，所以一个缓解办法就是使动作选择机制中的噪声于价值评估中的噪声去相关性，也就是 double-Q 学习。其核心思想就是不使用同一个网络来选择动作和评估价值，而是选择两个网络 \(\phi_{A}\) 和 \(\phi_{B}\)，训练过程如下：

\[ Q_{\phi_{A}}(\mathbf{s},\mathbf{a}) \leftarrow r+\gamma Q_{\phi_{B}}(\mathbf{s}',\arg \max_{\mathbf{a}'}Q_{\phi_{A}}(\mathbf{s}',\mathbf{a}')) \]

\[ Q_{\phi_{B}}(\mathbf{s},\mathbf{a}) \leftarrow r+\gamma Q_{\phi_{A}}(\mathbf{s}',\arg \max_{\mathbf{a}'}Q_{\phi_{B}}(\mathbf{s}',\mathbf{a}')) \]

这个系统具有修正更新的能力，也就是说训练过程中这两个网络会尽可能减小动作中正噪声带来的影响。

实际中并不需要额外添加一个 Q 函数，而是实际上使用我们已经拥有的两个 Q 函数 \(\phi,\phi'\) 。只要他们不是那么相似，就可以认为其去相关。

\[ y = r+\gamma Q_{\phi'}(\mathbf{s}',\arg \max_{\mathbf{a'}}Q_{\phi}(\mathbf{s}',\mathbf{a}')) \]

还有一种方法，采用多步回报：

\[ y_{i,t}= \sum_{t=t'}^{t+N-1} \gamma^{t-t'}r_{j,t'} +\gamma^{N}\max_{\mathbf{a}_{j,t+N}}Q_{\phi'}(\mathbf{s}_{j,t+N},\mathbf{a}_{j,t+N}) \]

这是从 Actor-critic 算法得到的启发，当 \(N=1\) 时，存在一定偏差但方差较低。其优点是当 Q 值不准确时，会给出一个低偏差的解；但这是一个在线算法。

当考虑连续动作时，会遇到一个问题：对连续动作做 \(\arg \max\) 这个操作并不是一件容易的事，这种事情主要发生在评估策略和计算目标值这两个方面，尤其在训练的内循环中，取 \(\max\) 操作会降低训练效率

一种解决办法是采用连续优化过程，比如在训练过程中采用梯度下降方法，但这个方法的效率比较低，考虑到动作空间一般是低维的，一个更好的解决方法是采用无导数的梯度下降法。一个简单的方法是将连续空间离散化：

\[ \max_{\mathbf{a}}Q(\mathbf{s},\mathbf{a}) \approx \max\left\{ Q(\mathbf{s},\mathbf{a}_{1}),\dots,Q(\mathbf{s},\mathbf{a}_{N}) \right\} \]

\(\mathbf{a}_{1},\dots,\mathbf{a}_{N}\) 是按某些分布（比如均匀分布）采样的。这种方法的好处是其非常简单，容易并行，缺点是没有那么准确，但是，考虑到 \(Q\) 函数本身会给出过大的估计，低准确性并不是一件坏事。更精确的方法可以采用交叉熵方法（CEM），这个方法能够优化我们的采样分布；CMA-ES 算法，这个算法可以视作更高级的 CEM 方法。

另一种解决方法是采用一个便于处理的函数类，比如说如下的二次函数：

\[ Q_{\phi}(\mathbf{s},\mathbf{a}) =- \frac{1}{2}(\mathbf{a}-\mu_{\phi}(\mathbf{s}))^{T}P_{\phi(\mathbf{s})}(\mathbf{a}-\mu_{\phi}(\mathbf{s}))+V_{\phi}(\mathbf{s}) \]

这个是由 Shixiang Gu 提出来的一种模型，称为 Normalized Advantage Function （NAF） 框架。在训练中，其神经网络给出三个值：一个标量偏差，一个向量值和一个矩阵值，他们定义了动作中的一个二次函数。因此可以找到最大值：

\[ \arg \max_{\mathbf{a}}Q_{\phi}(\mathbf{s},\mathbf{a}) = \mu_{\phi}(\mathbf{s})\quad \max_{\mathbf{a}}Q_{\phi}(\mathbf{s},\mathbf{a}) = V_{\phi}(\mathbf{s}) \]

他的好处是没有改变算法，效率和 Q 学习一样高，但如果 Q 函数并不是形如二次函数的话，他会损失一些表达能力。

第三种方法是学一个近似的最大化器，也就是训练一个网络使得：\(\mu_{\theta}(\mathbf{s})\approx\arg \max_{\mathbf{a}}Q_{\phi}(\mathbf{s,\mathbf{a}})\) ，这个过程实际上就是求解 \(\theta \leftarrow \arg \max_{\theta}Q_{\phi}(\mathbf{s},\mu_{\theta}(\mathbf{s}))\) 新目标值写作：

\[ y_{j}=r_{j}+\gamma Q_{\phi'}(\mathbf{s}_{j}',\mu_{\theta}(\mathbf{s}_{j}'))\approx r_{j}+\gamma Q_{\phi'}(\mathbf{s}'_{j},\arg \max_{\mathbf{a}'}Q_{\phi'}(\mathbf{s}_{j}',\mathbf{a}'_{j})) \]

具体算法如下：

Tip

slides 和 video 还有一点内容是讲一点作业的 tips 和 Q学习相关的论文，听不动了就没整 :D