Optimal Control and Planning
约 5533 个字 3 张图片 预计阅读时间 37 分钟
slides
笔记参考:CS285 深度强化学习 (8): Optimal Control and Planning - 知乎
之前讨论的都是 Model-free 的方法,现在讨论一些基于模型的算法。我们先讨论最优控制和规划的算法,这些方法假设可以访问系统的已知模型,并利用模型来做出决策。
在 Model-free 强化学习算法中,我们的目标是:
\[
\theta ^{*} = \arg \max_{\theta}\mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t=1}^{T} r(\mathbf{s}_{t},\mathbf{a}_{t}) \right]
\]
其中
\[
p_{\theta}(\tau) = p(\mathbf{s}_{1})\prod_{t=1}^{T}\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})
\]
在之前学习的算法中,我们假设不知道转移概率 \(p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\) ,也不打算学习它 ,所以这些算法仅通过从给定 \(\mathbf{s}_{t}\) 的完整轨迹中采样来工作的,或者采用 Q 函数来规避这些问题。
但在很多问题中,我们能够很容易得到转移概率,比如说游戏、容易建模的物理系统、仿真环境;在有些情况下,即使我们不知道转移概率,却也很容易学习,比如说:系统辨识(System identification)、学习过程。知道这些转移概率会让事情变得更容易,我们可以采用更多更有效的算法。
基于模型的强化学习:我们首先学习转移概率,并利用其选择动作。
- 轨迹优化(trajectory optimization):选择一系列状态和动作以优化某些结果的具体问题
- 规划(Planning):考虑离散事物的多种可能性(连续空间可以看作是一种轨迹优化问题)
- 最优控制(Optimal control):选择优化某些奖励或最小化某些成本的控制
在这些方法中,我们不再考虑策略,而是只有状态和动作。考虑一个遇到老虎的情形,我们的目标就是选择一些列动作最小化被老虎吃掉的概率,我们并不关心结果,只关心这些动作选择(决定会不会被吃),那么这是一个规划或轨迹优化问题。我们的目标是最小化成本总和或者最大化奖励总和,如果考虑这是一个无约束优化问题,我们实际上并没有考虑未来状态受过去事情影响这件事,所以这是一个约束优化问题,约束为每个连续状态都受前一状态和动作影响,即:
\[
\min_{\mathbf{a}_{1},\dots,\mathbf{a}_{T}} \sum_{t=1}^{T}c(\mathbf{s}_{t},\mathbf{a}_{t}) \quad \mathrm{s.t}\, \mathbf{s}_{t} = f(\mathbf{s}_{t-1},\mathbf{a}_{t-1})
\]
先考虑一个确定性状态(Deterministic case)。 假定一个智能体与环境交互,环境告诉智能体当前的状态 \(\mathbf{s}_{1}\) ,智能体会选择一系列动作并输出,这些动作满足:
\[
\mathbf{a}_{1},\dots,\mathbf{a}_{T}= \arg \max_{\mathbf{a_{1}},\dots,\mathbf{a}_{T}} \sum_{t=1}^{T} r(\mathbf{s}_{t},\mathbf{a}_{t}) \quad \mathrm{s.t.} \, \mathbf{a}_{t+1}=f(\mathbf{s}_{t},\mathbf{a}_{t})
\]
在随机状态下,定义
\[
p_{\theta}(\mathbf{s}_{1},\dots,\mathbf{s}_{T}|\mathbf{a}_{1},\dots,\mathbf{a}_{T})=p(\mathbf{s}_{1})\prod_{t=1}^{T}p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})
\]
所以输出的动作应该满足:
\[
\mathbf{a}_{1},\dots,\mathbf{a}_{T}= \arg \max_{\mathbf{a_{1}},\dots,\mathbf{a}_{T}}\mathbb{E}\left[ \sum_{t}r(\mathbf{s}_{t},\mathbf{a}_{t})| \mathbf{a}_{1},\dots,\mathbf{a}_{T} \right]
\]
但某些情况下,这并不是一个好的选择,或者说这是次优的(suboptimal)。例如一个简单的数学考试,在不知道题目的时候,会考虑尽可能答出每一道的答案,而这件事情会带来糟糕的奖励回报,因为你可能写下的每一个可能的答案序列很可能错误的。因此这个方法不适合用在那些未来会给出有助于选择动作信息的时候,
- 闭环(closed-loop):每观察到一个状态,采取一个动作
- 开环(open-loop):观察初始状态,采取一系列动作,暂时不关心新的状态。
在确定性的情况下,开环规划可能是一个很好的选择;但是在随机状态中,开环规划通常是次优的。在闭环状态下,目标函数可转换为 model-free 中的目标函数,只不过我们已知转移概率:
\[
\begin{align}
p(\mathbf{s}_{1},\mathbf{a}_{1},\dots \mathbf{s}_{T},\mathbf{a}_{T})& = \prod^{T}_{t=1}\pi(\mathbf{a}_{t}|\mathbf{s}_{t})p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t}) \\
\pi&= \arg \max_{\pi}\mathbb{E}_{\tau \sim p(\tau)}\left[ \sum_{t}^{} r(\mathbf{s}_{t},\mathbf{a}_{t}) \right]
\end{align}
\]
\(\pi\) 可以是我们之前讨论的神经网络,这是一个全局的方法,考虑到随机扰动问题,采用局部随时间变化的线性函数: \(\mathbf{K}_{t}\mathbf{s}_{t}+\mathbf{k}_{t}\)
Open-Loop Planning
开环规划有的时候是一个相当不错的方法。将最优控制或规划问题抽象成如下表示:
\[
\mathbf{a}_{1},\dots,\mathbf{a}_{T} =\arg \max_{\mathbf{a}_{1},\dots,\mathbf{a}_{T}}J(\mathbf{a}_{1},\dots,\mathbf{a}_{T})
\]
记:\(\mathbf{A}=[\mathbf{a}_{1},\dots,\mathbf{a}_{T}]\) ,于是问题变成:
\[
\mathbf{A}= \arg \max_{\mathbf{A}}J(\mathbf{A})
\]
我们采用的是一个黑箱优化方法,也就是说我们并不关心时间步长或者轨迹分布,我们只关心最大化问题。上面是一个无约束优化问题。
解决这个问题的一个简单方法是 guess and check
guess and check
- 在给定分布上采样 \(\mathbf{A}_{1},\dots,\mathbf{A}_{N}\)
- 计算 \(J(\mathbf{A}_{1}),\dots,J(\mathbf{A_{N}})\) ,选择最佳序列
这个方法也被称为 "random shooting method",尽管这看起来很简单, 但是在一些低维, short horizon 的简单任务是可行的, 而且这可以很容易实现,且很容易并行化,在现代硬件 上可以非常高效。缺点是可能会选择不太好的动作。
可以采用交叉熵改进上面的方法,对于一些低到中等维度、低到中等时间范围的黑箱优化方法,交叉熵方法是一个不错的选择。在 guess and check 的基础上改进我们的分布,也就是将我们的分布朝着能够带来更高的 \(J(\mathbf{A})\) 的区域拟合 。然后从新的分布再度抽样,再度拟合。
cross-entropy method with continuous-valued inputs
- 在给定分布上采样 \(\mathbf{A}_{1},\dots,\mathbf{A}_{N}\)
- 计算 \(J(\mathbf{A}_{1}),\dots,J(\mathbf{A_{N}})\)
- 选择最优序列 \(\mathbf{A}_{i_{1}},\dots \mathbf{A}_{i_{M}}\) ,其中 \(M<N\)
- 用这些最好的样本拟合一个新的分布 \(p(\mathbf{A})\)
一种连续分布的选择是高斯分布。也有更好的方式,如:CMA-ES。
这些方法的优点有:并行时速度特别块,实现简单,但问题是这些方法有相当严格的维度限度,也只能产生开环规划。
蒙特卡洛树搜索可以适应离散和连续状态,也能产生闭环规划。
假定一个模型,从初始状态 \(\mathbf{s}_{1}\) 开始, 每一个状态对应两个动作选择,每一个动作选择进入一个新的状态,对于每一个状态重新采取动作,重复这些行为,也许能够找到最优解,但是这是一个指数级的过程,这种无限制的无约束树搜索在每一层都是指数级的展开,这并不是一个好事情。所以问题变成了如何避免展开整棵树的同时尽可能估计状态的价值。一种方式当展开到某个节点时,运行一些基准策略,这些推演策略带来的价值并不是真的采取对应动作时带来的价值,而时对这些状态好坏的估计,比如说一个表现不佳的状态对应糟糕的价值。
由于我们的策略是随机的,状态也是随机的,所以这推演策略在相同状态采取相同动作给出的价值可能是不同的。因此,直觉上我们应该选择那些给出比较高回报的节点进行搜索,但同时也要搜索那些搜索比较少的节点,这是因为我们没法确定它的回报究竟是更好还是更差。
generic MCTS search
- 使用 \(\mathrm{TreePolicy}({s}_{1})\) 找到叶节点 \({s}_{l}\)
- 利用 \(\mathrm{DefaultPolicy}({s}_{l})\) 估计 \(\mathbf{s}_{l}\) 的价值
- 更新 \(\mathbf{s}_{1}\) 到 \(\mathbf{s}_{l}\) 的路径上所有节点的价值
这里的 \(s\) 表示时间序列。 \(\mathrm{DefaultPolicy}\) 是一个随机策略,\(\mathrm{TreePolicy}\) 常见选择是 UCT,也就是
- 如果 \(s_{t}\) 的动作有未被访问过的, 选择一个未被访问过的动作。
- 否则选择得分最高的动作 (最高的子节点)
UCT 的分数规则为:
\[
\mathrm{Score}(s_{t}) = \frac{Q(s_{t})}{N(s_{t})} +2C \sqrt{ \frac{2\ln N(s_{t-1})}{N(s_{t})} }
\]
这里的 \(Q\) 表示得分的累计,\(N\) 表示访问的次数。这个分数函数的思想就是,如果你探索某个节点的次数过少,那么你就会更倾向于优先探索新奇的节点。
Trajectory Optimization with Derivatives
现在关注基于导数的轨迹优化问题。
在最优控制领域,考虑的问题为:
\[
\min_{\mathbf{u}_{1},\dots,\mathbf{u}_{T}} \sum_{t=1}^{T}c(\mathbf{x}_{t},\mathbf{u}_{t}) \quad \mathrm{s.t}\, \mathbf{x}_{t} = f(\mathbf{x}_{t-1},\mathbf{u}_{t-1})
\]
其中 \(\mathbf{x}_{t}\) 表示的状态 \(\mathbf{u}_{t}\) 表示对应采取的动作。更改符号只是为了贴近控制领域相关的内容。将上面的约束优化问题转为如下无约束优化问题:
\[
\min_{\mathbf{u}_{1},\dots,\mathbf{u}_{T}} c(\mathbf{x}_{1},\mathbf{u}_{1})+c(f(\mathbf{x}_{1},\mathbf{u}_{1}),\mathbf{u}_{2})+\dots+ c(f(f(\dots)\dots),\mathbf{u}_{T})
\]
因此,为了利用导数求解上述无约束优化问题,需要知道:
\[
\frac{{\rm{d}} f }{{\rm {d}} \mathbf{x}_{t} } \quad \frac{{\rm{d}} f }{{\rm {d}} \mathbf{u}_{t} } \quad\frac{{\rm{d}} c }{{\rm {d}} \mathbf{x}_{t} } \quad \frac{{\rm{d}} c }{{\rm {d}} \mathbf{u}_{t} }
\]
如果采用一阶梯度下降方法,效果并不是很好,因此采用二阶梯度下降方法,实际上,在牛顿法情况,这个问题有一个更为简便的方法。 讨论如下两种优化方法
射击法(shooting method) 是一个基于动作的优化方法,也就是说仅对 \(\mathbf{u}_{t}\) 进行优化。这个方法对早期的动作比较敏感,后面的动作对其影响较小,其对应的 Hessian 矩阵特征值大的部分对应着较早的动作,特征值小的部分对应较晚的动作,从而导致数值不稳定,采用一阶梯度下降方法并不能缓解这个问题。

配点法(collocation)是一种在优化动作和状态的同时还加入额外约束的方法。对于这类问题,你的动作并不不会对动作轨迹末端产生较大的影响。因此数值更为稳定,可以使用一阶梯度下降。

回到我们的优化问题,考虑如下线性情况:(确定性情况)
\[
f(\mathbf{x}_{t},\mathbf{u}_{t}) = \mathbf{F}_{t}\begin{bmatrix}
\mathbf{x}_{t} \\
\mathbf{u}_{t}
\end{bmatrix}+\mathbf{f}_{t}
\]
假定代价函数为二次函数:
\[
c(\mathbf{x}_{t},\mathbf{u}_{t}) =\frac{1}{2}\begin{bmatrix}
\mathbf{x}_{t} \\
\mathbf{u }_{t}
\end{bmatrix}^{T}\mathbf{C}_{t}\begin{bmatrix}
\mathbf{x}_{t} \\
\mathbf{u }_{t}
\end{bmatrix}+\begin{bmatrix}
\mathbf{x}_{t} \\
\mathbf{u }_{t}
\end{bmatrix}^{T}\mathbf{c}_{t}
\]
我们允许 \(\mathbf{F}_{t},\mathbf{f}_{t},\mathbf{C}_{t},\mathbf{c}_{t}\) 随时间变化,将其带入无约束优化问题中。先考虑一个基本情况:仅求解 \(\mathbf{u}_{T}\)
取第 \(t\) 时间步位于 \(\mathbf{x}_{t}\),采取 \(\mathbf{u}_{t}\) 的代价函数:
\[
Q(\mathbf{x}_{T},\mathbf{u}_{T})= \mathrm{const}+ \frac{1}{2}\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{u}_{T}
\end{bmatrix}^{T}\mathbf{C}_{T}\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{u}_{T}
\end{bmatrix}+\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{u}_{T}
\end{bmatrix}^{T}\mathbf{c}_{T}
\]
根据 \(\mathbf{x}_{T},\mathbf{u}_{T}\) 可以将 \(\mathbf{C}_{T},\mathbf{c}_{T}\) 展开成分块矩阵和分块向量
\[
\mathbf{C}_{T} = \begin{bmatrix}
\mathbf{C}_{\mathbf{x}_{t},\mathbf{x}_{t}} & \mathbf{C}_{\mathbf{x}_{t},\mathbf{u}_{t}} \\
\mathbf{C}_{\mathbf{u}_{t},\mathbf{x}_{t}} & \mathbf{C}_{\mathbf{u}_{t},\mathbf{u}_{t}}
\end{bmatrix} \quad \mathbf{c}_{T}= \begin{bmatrix}
\mathbf{c}_{\mathbf{x}_{T}} \\
\mathbf{c}_{\mathbf{u}_{T}}
\end{bmatrix}
\]
最优解对应导数取零:
\[
\nabla_{\mathbf{u}_{T}}Q(\mathbf{x}_{T},\mathbf{u}_{T})= \mathbf{C}_{\mathbf{u}_{t},\mathbf{x}_{t}} \mathbf{x}_{T}+\mathbf{C}_{\mathbf{u}_{t},\mathbf{u}_{t}}\mathbf{u}_{T}+\mathbf{c}_{\mathbf{u}_{T}} = 0 \implies \mathbf{u}_{T} = -\mathbf{C}_{\mathbf{u}_{t},\mathbf{u}_{t}}^{-1}(\mathbf{C}_{\mathbf{u}_{t},\mathbf{x}_{t}} \mathbf{x}_{T}+\mathbf{c}_{\mathbf{u}_{T}})
\]
这就是最优动作的最优选择,显然这个最优动作依赖于 \(\mathbf{x}\) ,我们将 \(\mathbf{u}_{T}\) 简化成如下形式:
\[
\mathbf{u}_{T} = \mathbf{K}_{T}\mathbf{x}_{T} +\mathbf{k}_{T}
\]
其中:
\[
\mathbf{K}_{T}= -\mathbf{C}_{\mathbf{u}_{T},\mathbf{u}_{T}}\mathbf{C_{\mathbf{u}_{t},\mathbf{x}_{t}} }+\mathbf{c}_{\mathbf{u}_{T}} \quad \mathbf{k}_{T} = -\mathbf{C}^{-1}_{\mathbf{u}_{T},\mathbf{u}_{T}} \mathbf{c}_{\mathbf{u}_{T}}
\]
现在求解 \(\mathbf{x}_{T}\) 考虑到 \(\mathbf{u}_{T}\) 完全由 \(\mathbf{x}_{T}\) 决定,将 \(\mathbf{u}_{T}\) 替换得:
\[
V(\mathbf{x}_{T})= \mathrm{const}+ \frac{1}{2}\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{K}_{T}\mathbf{x}_{T} +\mathbf{k}_{T}
\end{bmatrix}^{T}\mathbf{C}_{T}\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{K}_{T}\mathbf{x}_{T} +\mathbf{k}_{T}
\end{bmatrix}+\begin{bmatrix}
\mathbf{x}_{T} \\
\mathbf{K}_{T}\mathbf{x}_{T} +\mathbf{k}_{T}
\end{bmatrix}^{T}\mathbf{c}_{T}
\]
观察得 \(V(\mathbf{x}_{T})\) 完全由 \(\mathbf{x}_{T}\) 的线性项和二次项组成,因此将上式化简成:
\[
V(\mathbf{x}_{T}) = \mathrm{const } + \frac{1}{2}\mathbf{x}_{T}^{T}\mathbf{V}_{T}\mathbf{x}_{T} +\mathbf{x}_{T}^{T}\mathbf{v}_{T}
\]
其中
\[
\begin{align}
\mathbf{V }_{t} &= \mathbf{C}_{\mathbf{x}_{T},\mathbf{x}_{T}} +\mathbf{C}_{\mathbf{x}_{T},\mathbf{u}_{T}} \mathbf{K }_{T}+\mathbf{K}_{T}^{T}
\mathbf{C}_{\mathbf{u}_{T},\mathbf{x}_{T}} +\mathbf{K}^{T}_{T}\mathbf{C}_{\mathbf{u}_{T},\mathbf{u}_{T}}\mathbf{K}_{T} \\
\mathbf{v}_{T}&= \mathbf{c}_{\mathbf{x}_{T}}+\mathbf{C}_{\mathbf{x}_{T},\mathbf{u}_{T}}\mathbf{k}_{T}+\mathbf{K }^{T}_{T}\mathbf{c}_{\mathbf{u}_{T}}+\mathbf{K}^{T}_{T}\mathbf{C}_{\mathbf{u}_{T},\mathbf{u}_{T}}\mathbf{k_{T}}
\end{align}
\]
现在推导由 \(\mathbf{x}_{T-1}\) 和 \(\mathbf{x}_{T}\) 给出 \(\mathbf{u}_{T-1}\)
约束条件给出:
\[
f(\mathbf{x}_{T-1},\mathbf{u}_{T-1}) = \mathbf{F}_{T-1}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}+\mathbf{f}_{T-1}
\]
此时
\[
\begin{align}
Q(\mathbf{x}_{T-1},\mathbf{u}_{T-1})= \mathrm{const}&+ \frac{1}{2}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{C}_{T-1}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}+\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{c}_{T-1} \\
&+V(f(\mathbf{x}_{T-1},\mathbf{u}_{T-1}))
\end{align}
\]
\[
\begin{align}
V(\mathbf{x}_T)= \mathrm{const} + \frac{1}{2}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{F}_{T-1}^{T} \mathbf{V}_{T}\mathbf{F}_{T-1}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix} \\
+\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T} \mathbf{F}_{T-1}\mathbf{V}_{T} \mathbf{f}_{T-1}+\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{F}^{T}_{T-1}\mathbf{v}_{T}
\end{align}
\]
带回可以得到:
\[
Q(\mathbf{x}_{T-1},\mathbf{u}_{T-1} )= \mathrm{const} + \frac{1}{2}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{Q}_{T-1}\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}+\begin{bmatrix}
\mathbf{x}_{T-1} \\
\mathbf{u}_{T-1}
\end{bmatrix}^{T}\mathbf{q}_{T-1}
\]
其中
\[
\mathbf{Q}_{T-1} = \mathbf{C}_{T-1}+\mathbf{F}_{T-1}^{T} \mathbf{V}_{T}\mathbf{F}_{T-1} \quad \mathbf{q}_{T-1}=\mathbf{c}_{T-1}+\mathbf{F}_{T-1}^{T} \mathbf{V}_{T}\mathbf{f}_{T-1}+\mathbf{F}_{T-1}^{T}\mathbf{v}_{T}
\]
同样求导去零可得
\[
\mathbf{u}_{T-1} = \mathbf{K}_{T-1}\mathbf{x}_{T-1}+\mathbf{k}_{T-1}
\]
其中:
\[
\mathbf{K}_{T-1}= - \mathbf{Q}^{-1}_{\mathbf{u}_{T-1},\mathbf{u}_{T-1}}\mathbf{Q}_{\mathbf{u}_{T-1},\mathbf{x}_{T-1}} \quad \mathbf{k}_{T-1}=- \mathbf{Q}^{-1}_{\mathbf{u}_{T-1},\mathbf{u}_{T-1}}\mathbf{q}_{\mathbf{u}_{T-{1}}}
\]
从 \(t=T-1\) 到 \(t=1\) 的部分推导过程是完全类似的。
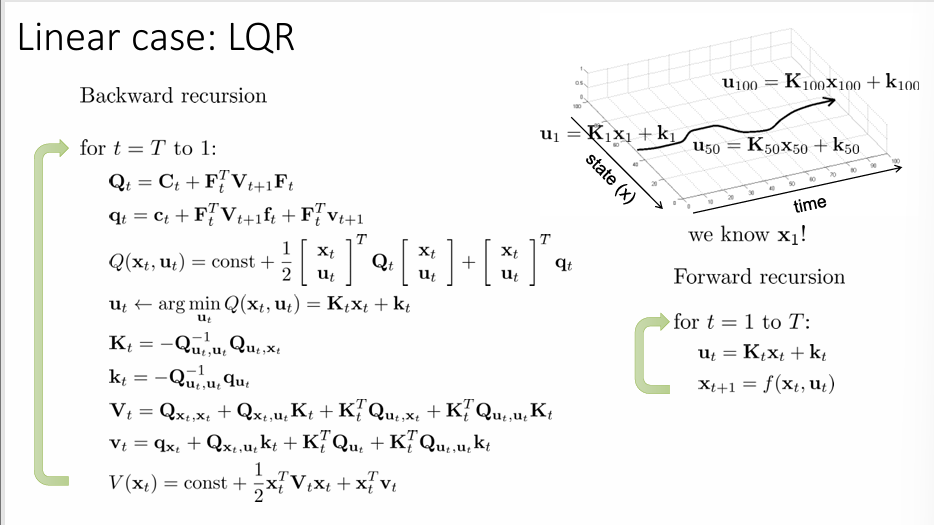
Backward recursion
对 \(t=T\) 到 \(1\)
\(\mathbf{Q}_{t} = \mathbf{C}_{t}+\mathbf{F}_{t}^{T}\mathbf{V}_{t+1}\mathbf{F}_{t}\)
\(\mathbf{q}_{t} = \mathbf{c}_{t}+\mathbf{F}_{t}^{T}\mathbf{V}_{t+1}\mathbf{f}_{t}+\mathbf{F}_{t}^{T}\mathbf{v}_{t+1}\)
\(Q(\mathbf{x}_{t},\mathbf{u}_{t} )= \mathrm{const} + \frac{1}{2}\begin{bmatrix}\mathbf{x}_{t} \\\mathbf{u}_{t}\end{bmatrix}^{T}\mathbf{Q}_{t}\begin{bmatrix}\mathbf{x}_{t} \\\mathbf{u}_{t}\end{bmatrix}+\begin{bmatrix}\mathbf{x}_{t} \\\mathbf{u}_{t}\end{bmatrix}^{T}\mathbf{q}_{t}\)
\(\mathbf{u}_{t}\leftarrow \arg \min_{\mathbf{u}_{t}} Q(\mathbf{x}_{t},\mathbf{u}_{t})=\mathbf{K}_{t}\mathbf{x}_{t}+\mathbf{k}_{t}\)
\(\mathbf{K}_{t}= - \mathbf{Q}^{-1}_{\mathbf{u}_{t},\mathbf{u}_{t}}\mathbf{Q}_{\mathbf{u}_{t},\mathbf{x}_{t}}\)
\(\mathbf{k}_{t}=- \mathbf{Q}^{-1}_{\mathbf{u}_{t},\mathbf{u}_{t}}\mathbf{q}_{\mathbf{u}_{T-{1}}}\)
\(\mathbf{V}_{t}=\mathbf{Q}_{\mathbf{x}_{t},\mathbf{x}_{t}}+\mathbf{Q}_{\mathbf{x}_{t},\mathbf{u}_{t}}\mathbf{K}_{t}+\mathbf{K}_{t}^{T}\mathbf{Q}_{\mathbf{u}_{t},\mathbf{x}_{t}}+\mathbf{K}^{T}_{t}\mathbf{Q}_{\mathbf{u}_{t},\mathbf{u}_{t}}\mathbf{K}_{t}\)
\(\mathbf{v}_{t}=\mathbf{q}_{\mathbf{x}_{t}}+\mathbf{Q}_{\mathbf{x}_{t},\mathbf{u}_{t}}\mathbf{k}_{t}+\mathbf{K}_{t}^{T}\mathbf{Q}_{\mathbf{u}_{t}}+\mathbf{K}^{T}_{t}\mathbf{Q}_{\mathbf{u}_{t},\mathbf{u}_{t}}\mathbf{k}_{t}\)
\(V(\mathbf{x}_{t}) = \mathrm{const}+\frac{1}{2}\mathbf{x}_{t}^{T}\mathbf{V}_{t}\mathbf{x}_{t}+\mathbf{x}_{t}^{T}\mathbf{v}_{t}\)
当回溯到 \(t=1\) 时,我们已经知道 \(\mathbf{x}_{1}\) ,因此可以向前递归:
Forward recursion
对 \(t=1\) 到 \(T\)
\(\mathbf{u}_{t}=\mathbf{K}_{t}\mathbf{x}_{t}+\mathbf{k}_{t}\)
\(\mathbf{x}_{t+1}= f(\mathbf{x}_{t},\mathbf{u}_{t})\)
上面的内容正是 LQR(Linear-Quadratic Regulator) ,这是一个最经典的确定性最优控制方法,解决的是一个“线性系统”与“二次代价”的问题。
LQR for Stochastic and Nonlinear Systems
现在考虑随机动力学的情况,状态带入如下的高斯分布:
\[
\mathbf{x}_{t+1} \sim \mathcal{N}(f(\mathbf{x}_{t},\mathbf{u}_{t}),\Sigma_{t})
\]
其中
\[
f(\mathbf{x}_{t},\mathbf{u}_{t}) = \mathbf{F}_{t}\begin{bmatrix}
\mathbf{x}_{t} \\
\mathbf{u}_{t}
\end{bmatrix}+\mathbf{f}_{t}
\]
尽管由于随机噪声的影响,访问的状态实际上是随机的,因此无法生成单一的开环序列,但是仍可以将最优动作表示为如下形式:
\[
\mathbf{u}_{t}=\mathbf{K}_{t}\mathbf{x}_{t}+\mathbf{k}_{t}
\]
也就是算法本身没有改变,\(\Sigma_{t}\) 的影响由于高斯分布的对称性抵消了。参考笔记中对此有详细的证明。
在非线性的情况,将 LQR 算法进行拓展,可以得到一个被称为微分动态规划(DDP)或迭代 LQR 算法。
将 dynamic 和 cost 展开成如下形式:
\[
f(\mathbf{x}_{t},\mathbf{u}_{t}) \approx f(\hat{\mathbf{x}}_{t}+\hat{\mathbf{u}}_{t})+\nabla_{\mathbf{x}_{t},\mathbf{u}_{t}}f(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\begin{bmatrix}
\mathbf{x}_{t} - \hat{\mathbf{x}}_{t} \\
\mathbf{u}_{t} - \hat{\mathbf{u}}_{t}
\end{bmatrix}
\]
\[
\begin{align}
{c}(\mathbf{x}_{t},\mathbf{u}_{t})\approx c(\hat{\mathbf{x}}_{t}+\hat{\mathbf{u}}_{t})+\nabla_{\mathbf{x}_{t},\mathbf{u}_{t}}c(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\begin{bmatrix}
\mathbf{x}_{t} - \hat{\mathbf{x}}_{t} \\
\mathbf{u}_{t} - \hat{\mathbf{u}}_{t} \\
\end{bmatrix} \\
+ \frac{1}{2} \begin{bmatrix}
\mathbf{x}-\hat{\mathbf{x}}_{t} \\
\mathbf{u}-\hat{\mathbf{u}_{t}}
\end{bmatrix}^{T}\nabla^{2}_{\mathbf{x}_{t},\mathbf{u}_{t}}c(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\begin{bmatrix}
\mathbf{x}_{t} - \hat{\mathbf{x}}_{t} \\
\mathbf{u}_{t} - \hat{\mathbf{u}}_{t} \\
\end{bmatrix}
\end{align}
\]
记 \(\delta \mathbf{x}_{t}=\mathbf{x}_{t}-\hat{\mathbf{x}}_{t},\delta \mathbf{u}_{t}=\mathbf{u}_{t}-\hat{\mathbf{u}}_{t}\) ,则将线性二次系统写作偏差形式:
\[
\bar{f}(\mathbf{x}_{t},\mathbf{u}_{t}) = \mathbf{F}_{t}\begin{bmatrix}
\delta\mathbf{x}_{t} \\
\delta\mathbf{u}_{t}
\end{bmatrix}
\]
\[
\bar{c}(\delta\mathbf{x}_{t},\delta\mathbf{u}_{t}) =\frac{1}{2}\begin{bmatrix}
\delta\mathbf{x}_{t} \\
\delta\mathbf{u }_{t}
\end{bmatrix}^{T}\mathbf{C}_{t}\begin{bmatrix}
\delta\mathbf{x}_{t} \\
\delta\mathbf{u }_{t}
\end{bmatrix}+\begin{bmatrix}
\delta\mathbf{x}_{t} \\
\delta\mathbf{u }_{t}
\end{bmatrix}^{T}\mathbf{c}_{t}
\]
这就是迭代 LQR 算法
iterative LQR
直到收敛:
\(\mathbf{F}_{t} = \nabla_{\mathbf{x_{t},\mathbf{u}_{t}}}f(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\)
\(\mathbf{C}_{t}=\nabla^{2}_{\mathbf{x}_{t},\mathbf{u}_{t}}c(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\)
\(\mathbf{c}_{t}=\nabla_{\mathbf{x}_{t},\mathbf{u}_{t}}c(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\)
利用 \(\delta \mathbf{x}_{t},\delta \mathbf{u}_{t}\) 运行 LQR 的反向过程
利用 \(\mathbf{u}_{t} = \mathbf{K}_{t}\delta \mathbf{x}_{t}+\mathbf{k}_{t}+\hat{\mathbf{u}}_{t}\) 运行 LQR 的前行过程
基于前行结果的更新 \(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t}\)
原先的 LQR 并不是迭代的,只需要单次的 backward pass 与 forward pass 即可解得最优解。而 iterative LQR 是迭代的,每次迭代都会更新\(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t}\) 就如同在梯度下降中的更新参数一样迭代地进行。
与牛顿法进行比较,实际上 ILQR 算法的基本思想和牛顿法是一样的,我们通过泰勒展开得到了原始优化问题的一个近似,其与牛顿法的差别就在我们没有考虑 dynamics 的二阶导数展开,如果考虑二阶展开我们也就能够得到一个优雅的递归算法,即 DDP 。
二阶 dynamics 展开
\[
\begin{align}
f(\mathbf{x}_{t},\mathbf{u}_{t}) \approx f(\hat{\mathbf{x}}_{t}+\hat{\mathbf{u}}_{t})+\nabla_{\mathbf{x}_{t},\mathbf{u}_{t}}f(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\begin{bmatrix}
\mathbf{x}_{t} - \hat{\mathbf{x}}_{t} \\
\mathbf{u}_{t} - \hat{\mathbf{u}}_{t}
\end{bmatrix} \\
+ \frac{1}{2} \begin{bmatrix}
\mathbf{x}-\hat{\mathbf{x}}_{t} \\
\mathbf{u}-\hat{\mathbf{u}_{t}}
\end{bmatrix}^{T}\nabla^{2}_{\mathbf{x}_{t},\mathbf{u}_{t}}f(\hat{\mathbf{x}}_{t},\hat{\mathbf{u}}_{t})\begin{bmatrix}
\mathbf{x}_{t} - \hat{\mathbf{x}}_{t} \\
\mathbf{u}_{t} - \hat{\mathbf{u}}_{t} \\
\end{bmatrix}
\end{align}
\]
实际上这需要一个张量积,因为二阶 dynamics 是一个三维张量。
传统牛顿法采用如下方法更新参数:
\[
\hat{\mathbf{x}} \leftarrow \arg \min_{\mathbf{x}} \frac{1}{2}(\mathbf{x}-\hat{\mathbf{x}})^{T} \mathbf{H}(\mathbf{x}-\hat{\mathbf{x}})+\mathbf{g}^{T}(\mathbf{x}-\hat{\mathbf{x}})
\]
实际上这并不是一个很好的更新方式,在利用二次函数进行拟合时会造成一个现象是迭代的结果比起始点更糟糕,因为他有可能会产生了一定偏差了(实际上在数值分析中,牛顿法的收敛条件更为苛刻)。我们希望迭代结果能够回退一点(这能更接近最优解)。在 ILQR 算法中,我们希望先计算我们的解,然后检查这个解是否比原来的解好。
在前向传播中,我们添加一个常数 \(\alpha \in(0,1)\) 来控制偏离起始点的程度:
\[
\mathbf{u}_{t} = \mathbf{K}_{t}\delta \mathbf{x}_{t}+\alpha\mathbf{k}_{t}+\hat{\mathbf{u}}_{t}
\]
当减小 \(\alpha\) 时,我们会更接近原来的动作序列。
在时间中,我们既可以减少 \(\alpha\) 以至于新成本低于旧成本,也可以计算从二次近似中预期成本的改进,从而改变 \(\alpha\) 满足预期。还可以采用如括号线搜索等更多线搜索方法。


