Plane Problem Axisymmetric
约 2487 个字 2 张图片 预计阅读时间 17 分钟
2D Problem
二维问题的基本方程
平面应力问题(薄板)
\[
\begin{Bmatrix}
\varepsilon_{x} \\
\varepsilon_{y} \\
\gamma_{xy}
\end{Bmatrix} =\begin{bmatrix}
\frac{1}{E} & -\frac{\nu}{E} & 0 \\
-\frac{\nu}{E} & -\frac{1}{E} & 0 \\
0 & 0 & \frac{1}{G}
\end{bmatrix}\begin{Bmatrix}
\sigma_{x} \\
\sigma_{y} \\
\sigma_{xy}
\end{Bmatrix}
\]
其中 \(G =\frac{E}{2(1+\nu)}\)
\[
\begin{Bmatrix}
\sigma_{x} \\
\sigma_{y} \\
\tau_{xy}
\end{Bmatrix} =\frac{E}{1-\nu^{2}} \begin{bmatrix}
1 & \nu & 0 \\
\nu & 1 & 0 \\
0 & 0 & \frac{1-\nu}{2}
\end{bmatrix}\begin{Bmatrix}
\varepsilon_{x } \\
\varepsilon_{y} \\
\gamma_{xy}
\end{Bmatrix}
\]
对应平面应变问题(无限长物体),形式与平面应力问题形式相同,只需要做如下改动:
\[
E_{1} = \frac{E}{1-\nu^{2}} \quad \nu_{1}=\frac{\nu}{1-\nu}
\]
将应力应变关系记作原来的矩阵形式:
\[
{\sigma} = {D \varepsilon}
\]
\[
\begin{Bmatrix}
\varepsilon_{x} \\
\varepsilon_{y} \\
\gamma_{xy}
\end{Bmatrix} = \begin{bmatrix}
\frac{\partial }{\partial x } & 0 \\
0 & \frac{\partial }{\partial y } \\
\frac{\partial }{\partial y } & \frac{\partial }{\partial x }
\end{bmatrix}\begin{Bmatrix}
u \\
v
\end{Bmatrix} \triangleq {\varepsilon}=(\nabla \mathbf{u})
\]
我们称 \(\nabla\) 为梯度算子
\[
\begin{bmatrix}
\frac{\partial }{\partial x } & 0 & \frac{\partial }{\partial y } \\
0 & \frac{\partial }{\partial y } & \frac{\partial }{\partial x }
\end{bmatrix}\begin{Bmatrix}
\sigma_{x} \\
\sigma_{y} \\
\tau_{xy}
\end{Bmatrix}+\begin{Bmatrix}
f_{x} \\
f_{y}
\end{Bmatrix} = \begin{Bmatrix}
0 \\
0
\end{Bmatrix}\triangleq \nabla^{T} {\sigma}+\mathbf{f}=0
\]
\[
\begin{bmatrix}
n_{x} & 0 & n_{y } \\
0 & n_{y} & n_{x}
\end{bmatrix}\begin{Bmatrix}
\sigma_{x} \\
\sigma_{y} \\
\tau_{xy}
\end{Bmatrix}= \begin{Bmatrix}
\bar{T}_{x} \\
\bar{T_{y}}
\end{Bmatrix}\triangleq \mathbf{n}{\sigma} = \bar{\mathbf{T}}
\]
位移解法
在二维问题,位移插值可以写作如下形式:
\[
\begin{align}
u = \sum_{}^{} N_{i}u_{i} \\
v = \sum_{}^{} N_{i}v_{i}
\end{align}
\]
矩阵形式:
\[
\begin{Bmatrix}
u \\
v
\end{Bmatrix}= \begin{bmatrix}
N_{1} & 0 & N_{2} & 0 & \dots \\
0 & N_{1} & 0 & N_{2} & \dots
\end{bmatrix}\begin{Bmatrix}
u_{1} \\
v_{1} \\
u_{2} \\
v_{2} \\
\vdots
\end{Bmatrix}\triangleq \mathbf{u} = \mathbf{Nd}
\]
引入记号:
\[
\mathbf{B}= \nabla \mathbf{N}
\]
表征应变矩阵
\[
\Pi_{p} = U +\Omega_{b}+\Omega_{p}+\Omega_{s}
\]
\[
U = \frac{1}{2 }\mathbf{d}^{T}\left( \int_{V}\mathbf{B}^{T}\mathbf{DB}\,\mathrm{d} V\right) \mathbf{d}= \frac{1}{2}\mathbf{d}^{T}\mathbf{k}_{e}\mathbf{d}
\]
\(\mathbf{k}_{e}\) 称为刚度矩阵
\[
\Omega_{b} = - \int_{V}\mathbf{u}^{T}\mathbf{f}\,\mathrm{d}V=-\int_{V}(\mathbf{Nd})^{T}\mathbf{f}\,\mathrm{d}V = -\mathbf{d}^{T}\left( \int_{V}\mathbf{N}^{T}\mathbf{f}dV \right)
\]
\[
\Omega_{p} = - \mathbf{d}^{T}\mathbf{P}
\]
\[
\Omega_{s} = -\int_{S}\mathbf{u}^{T}\mathbf{T}_{s}\,\mathrm{d}S = -\int_{S} \left( \mathbf{Nd} \right) ^{T}\mathbf{T}_{s}\,\mathrm{d}S = -\mathbf{d}^{T}\left( \int_{S}\mathbf{N}^{T} \mathbf{T}_{s}\,\mathrm{d}S\right)
\]
将上述表达式带入后,最小势能原理给出:
\[
\frac{\delta \Pi_{p}}{\delta \mathbf{d}^{T}} =0
\]
可得:
\[
\mathbf{k}_{e}\mathbf{d} = \underset{ 体力的等效结点力 }{ \int_{V}\mathbf{N}^{T}\mathbf{f}\,\mathrm{d}V }+\underset{ 结点上的集中力 }{ \mathbf{P} }+\underset{ 面力的等效结点力 }{ \int_{S}\mathbf{N}^{T}\mathbf{T}_{s}\,\mathrm{d} S }
\]
CST
不同节点数的三角形元素可用于求解二维实体构件。线性三角形元素是为二维实体有限元分析开发的第一种元素。然而,与线性四边形元素相比,线性三角形元素的精确度较低。但三角形元素仍是一种非常有用的元素,因为它能适应复杂的几何形状。如果二维模型的几何形状非常复杂,就需要使用三角形元素。恒应变三角形(CST)是数学上最简单的元素。
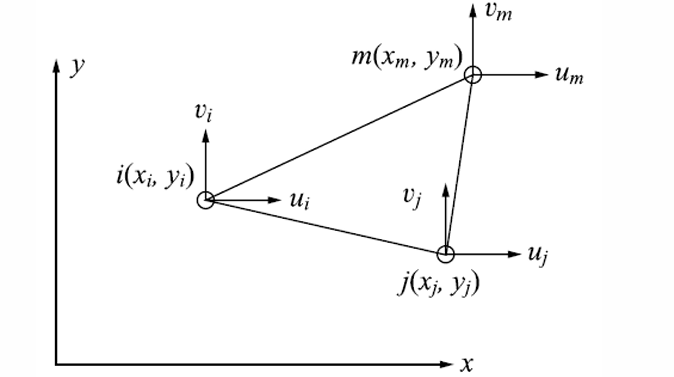
对应型函数:
\[
\begin{align}
u(x,y) = a_{1}+a_{2} x + a_{3}y \\
v(x,y) = a_{4}+a_{5}x+a_{6}y
\end{align}
\]
我们可以得到应变表达式:
\[
\varepsilon_{x}=a_{2},\varepsilon_{y}=a_{6},\gamma_{xy}= a_{3}+a_{5}
\]
可见应变都是常量,这就是为什么我们称为常应变三角形
求取参数:已知位移 \(u_{i},u_{j},u_{m},v_{i},v_{j},v_{m}\) 和坐标 \(x_{i},x_{j},x_{m},y_{i},y_{j},y_{m}\) 可确定 \(a_{1},a_{2},a_{3},a_{4},a_{5},a_{6}\) 的值(带入上述表达写成矩阵形式并取逆):
\[
\begin{Bmatrix}
a_{1} \\
a_{2} \\
a_{3}
\end{Bmatrix} = \frac{1}{2A}\begin{bmatrix}
\alpha_{i} & \alpha_{j} & \alpha_{m} \\
\beta_{i} & \beta_{j} & \beta_{m} \\
\gamma_{i} & \gamma_{j} & \gamma_{m}
\end{bmatrix}
\begin{Bmatrix}
u_{i} \\
u_{j} \\
u_{m}
\end{Bmatrix}
\quad
\begin{Bmatrix}
a_{4} \\
a_{5} \\
a_{6}
\end{Bmatrix} = \frac{1}{2A}\begin{bmatrix}
\alpha_{i} & \alpha_{j} & \alpha_{m} \\
\beta_{i} & \beta_{j} & \beta_{m} \\
\gamma_{i} & \gamma_{j} & \gamma_{m}
\end{bmatrix}\begin{Bmatrix}
v_{i} \\
v_{j} \\
v_{m}
\end{Bmatrix}
\]
其中
\[
2A = \begin{vmatrix}
1 & x_{i} & y_{i} \\
1 & x_{j} & y_{j} \\
1 & x_{m} & y_{m}
\end{vmatrix} = x_{i}(y_{i}-y_{m}) + x_{j}(y_{m}-y_{i})+x_{m}(y_{i}-y_{j})
\]
(考虑行列式的几何意义,可得 \(A\) 为三角形面积)
\[
\alpha_{i} =x_{j}y_{m}-x_{m}y_{j} \quad\alpha_{j}=x_{m}y_{i}-x_{i}y_{m}\quad \alpha_{m}=x_{i}y_{j}-x_{j}y_{i}
\]
\[
\beta_{i} =y_{j}-y_{m} \quad\beta_{j}=y_{m}-y_{i}\quad \beta_{m}=y_{i}-y_{j}
\]
\[
\gamma_{i} =x_{m}-x_{j} \quad\gamma_{j}=x_{i}-x_{m}\quad \gamma_{m}=x_{j}-x_{i}
\]
\[
\begin{align}
N_{i}&=(\alpha_{i}+\beta_{i}x+\gamma_{i}y)/2A \\
N_{j}&=(\alpha_{j}+\beta_{j}x+\gamma_{j}y)/2A \\
N_{m}&=(\alpha_{m}+\beta_{m}x+\gamma_{m}y)/2A
\end{align}
\]
\[
\begin{Bmatrix}
u \\
v
\end{Bmatrix}=\begin{bmatrix}
N_{i} & 0 & N_{j} & 0 & N_{m} & 0 \\
0 & N_{i} & 0 & N_{j} & 0 & N_{m}
\end{bmatrix}
\begin{Bmatrix}
u_{i} \\
v_{i} \\
u_{j} \\
v_{j} \\
u_{m} \\
v_{m}
\end{Bmatrix}\triangleq \mathbf{u} = \mathbf{Nd}
\]
\[
\begin{Bmatrix}
\varepsilon_{x} \\
\varepsilon_{y} \\
\gamma_{xy}
\end{Bmatrix}
=\frac{1}{2A}
\begin{bmatrix}
\beta _{i} & 0 & \beta_{j} & 0 & \beta_{m} & 0\\
0& \gamma_{i} & 0& \gamma_{j} & 0& \gamma_{m} \\
\gamma_{i} & \beta _{i} & \gamma_{j} & \beta_{j} & \gamma_{m} & \beta_{m}
\end{bmatrix}
\triangleq {\varepsilon} = \mathbf{Bd}
\]
\[
\mathbf{k}_{e} =\int_{V}\mathbf{B}^{T}\mathbf{DB}\,\mathrm{d}V = tA(\mathbf{B}^{T}\mathbf{DB})
\]
\(A\) 为元素的面积,\(t\) 为平板厚度,\(\mathbf{k}_{e}\) 式一个 \(6\times{6}\) 对称矩阵
\[
\mathbf{f}=\begin{bmatrix}
X_{b} \\
Y_{b}
\end{bmatrix}
\]
\[
\int_{V}\mathbf{N}^{T}\mathbf{f}\,\mathrm{d}V = \frac{At}{3}\begin{Bmatrix}
X_{b} \\
Y_{b} \\
X_{b} \\
Y_{b} \\
X_{b} \\
Y_{b} \\
\end{Bmatrix}
\]
也就是说,体力被均分在结点上
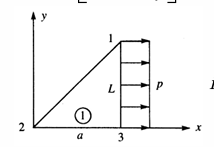
\[
\mathbf{T}_{s} = \begin{bmatrix}
p_{x} \\
p_{y}
\end{bmatrix}
\]
一个栗子是我们假定 \(p_{x}=p\) \(p_{y }=0\)
\[
\int_{S}\mathbf{N}^{T}\mathbf{T}_{s}\,\mathrm{d} S = tp \int \begin{Bmatrix}
N_{1}(a,y) \\
0 \\
N_{2}(a,y) \\
0 \\
N_{3} (a,y) \\
0
\end{Bmatrix}\,\mathrm{d} y
\]
取
\[
N_{1} = \frac{ay}{2A} \quad N_{2}=\frac{L(a-x)}{2A} \quad N_{3}=\frac{Lx-ay}{2A}
\]
则可得
\[
\int_{S}\mathbf{N}^{T}\mathbf{T}_{s}\,\mathrm{d} S = \begin{Bmatrix}
\frac{pLt}{2} \\
0 \\
0 \\
0 \\
\frac{pLt}{2} \\
0
\end{Bmatrix}
\]
Applications of the CST Element
- Use in areas where the strain gradient is small
- Use in mesh transition areas(fine mesh to coarse mesh)
- Avoid using CST in stress concentration or other crucial areas in the structure, such as edges of holes adn corners
- Recommended for quick and preliminary FE analysis of 2D problems
当然除了恒应变三角形之外,我们还有其他二元元素。
如果我们三角形的每个边上再取一个结点,则我们得到了线性应变三角形(Linear Strain Triangle,LST)。取对应位移表达式:
\[
u = a+bx +cy +dx^{2}+ey^{2}+fxy
\]
应变:
\[
\varepsilon _{x} =b +2d x+fy
\]
可以看出,应变是一个线性函数,他的结果比 CST 拟合效果更好。
矩形(四个结点):
\[
\begin{align}
u=a_{1}+a_{2}x+a_{3}y + a_{4}xy \\
v=a_{5}+a_{6}x+a_{7}y + a_{8}xy
\end{align}
\]
可以得出应变是一个线性函数
模仿LST,我们多取矩形边的中点,可得二次矩形,这是因为应变是二次形的。
- T3 : linear displacement, constant strain and stress;
- Q4: bilinear displacement, linear strain and stress;
- T6: quadratic displacement, linear strain and stress
- Q8: Cubic displacement, quadratic strain and stress.
Axisymmetric
对于轴对称问题,有:
\[
\frac{\partial (\cdot) }{\partial \theta } =0
\]
位移场:
\[
u=u(r,z) ,w =w(r,z)
\]
应变:
\[
\begin{Bmatrix}
\varepsilon_{r} \\
\varepsilon_{\theta} \\
\varepsilon_{z} \\
\gamma_{rz}
\end{Bmatrix} = \begin{bmatrix}
\frac{\partial }{\partial r } & 0 \\
\frac{1}{r} & 0 \\
0 & \frac{\partial }{\partial z } \\
\frac{\partial }{\partial z } & \frac{\partial }{\partial r }
\end{bmatrix}\begin{Bmatrix}
u \\
w
\end{Bmatrix}
\]
应力:
\[
\begin{Bmatrix}
\sigma_{r} \\
\sigma_{\theta} \\
\sigma_{z} \\
\tau_{rz}
\end{Bmatrix} = \frac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix}
1-\nu & \nu & \nu & 0 \\
\nu & 1-\nu & \nu & 0 \\
\nu & \nu & 1-\nu & 0 \\
0 & 0 & 0 & \frac{1-2\nu}{2}
\end{bmatrix}\begin{Bmatrix}
\varepsilon_{r} \\
\varepsilon_{\theta} \\
\varepsilon_{z} \\
\gamma_{rz}
\end{Bmatrix}
\]
采用CST划分:
\[
\begin{align}
u (r,z) &= a_{1}+a_{2}r+a_{3}z \\
w(r,z) &= a_{4}+a_{5}r+a_{6}z
\end{align}
\]
如果已知三点的位移 \(u_{i},u_{j},u_{m},w_{i},w_{j},w_{m}\),则同样可以定出:
\[
\begin{Bmatrix}
a_{1} \\
a_{2} \\
a_{3}
\end{Bmatrix}=\begin{bmatrix}
1 & r_{i} & z_{i} \\
1 & r_{j} & z_{j} \\
1 & r_{m} & z_{m} \\
\end{bmatrix}^{-1}\begin{Bmatrix}
u_{i} \\
u_{j} \\
u_{m}
\end{Bmatrix} \quad \begin{Bmatrix}
a_{4} \\
a_{5} \\
a_{6}
\end{Bmatrix}=\begin{bmatrix}
1 & r_{i} & z_{i} \\
1 & r_{j} & z_{j} \\
1 & r_{m} & z_{m} \\
\end{bmatrix}^{-1}\begin{Bmatrix}
u_{i} \\
u_{j} \\
u_{m}
\end{Bmatrix}
\]
\[
\begin{Bmatrix}
u \\
w
\end{Bmatrix}=
\begin{bmatrix}
N_{i} & 0 & N_{j} & 0 & N_{m} & 0 \\
0 & N_{i} & 0 & N_{j} & 0 & N_{m}
\end{bmatrix}
\begin{Bmatrix}
u_{i} \\
w_{i} \\
u_{j} \\
w_{j} \\
u_{m} \\
w_{m}
\end{Bmatrix}\triangleq \mathbf{u} = \mathbf{Nd}
\]
系数表达式与平面问题中讨论的相同
\[
\begin{Bmatrix}
\varepsilon_{r} \\
\varepsilon_{\theta} \\
\varepsilon_{z} \\
\gamma_{xy}
\end{Bmatrix} =\frac{1}{2A} \begin{bmatrix}
\beta_{i} & 0 & \beta _{j} & 0 & \beta_{m} & 0 \\
0 & \gamma_{i} & 0 & \gamma_{j} & 0 & \gamma_{m} \\
\frac{\alpha_{i}}{r}+\beta_{i}+\frac{\gamma_{i}z}{r} & 0 & \frac{\alpha_{j}}{r}+\beta_{i}+\frac{\gamma_{j}z}{r} & 0 & \frac{\alpha_{m}}{r}+\beta_{i}+\frac{\gamma_{m}z}{r} & 0 \\
\gamma_{i} & \beta_{i} & \gamma_{j} & \beta_{j} & \gamma_{m} & \beta_{m}
\end{bmatrix}\begin{Bmatrix}
u_{i} \\
w_{i} \\
u_{j} \\
w_{j} \\
u_{m} \\
w_{m}
\end{Bmatrix}
\]
记作
\[
{\varepsilon} = \mathbf{Bd}
\]
注意 \(1/r\) 项,此时对应的应变并非是一个恒定的数
\[
\mathbf{k}_{e} = 2\pi \int_{A} \mathbf{B}^{T}\mathbf{DB}r\mathrm{d}r\mathrm{d}z
\]
采用数值积分方法求解
\[
\begin{align}
f_{r} &= \rho r \omega^{2} \\
f_{z}&= - \rho g
\end{align}
\]
转换为节点力:
\[
\begin{align}
&\left\{ f_{b} \right\} = 2\pi \iint_{S} [\mathbf{N}]^{T}\begin{Bmatrix}
f_{r} \\
f_{z}
\end{Bmatrix}r\mathrm{d}r \mathrm{d}z \\
\implies&\left\{ f_{b} \right\} = \frac{2\pi \bar{r}A}{3}\begin{Bmatrix}
\bar{f_{r}} \\
f_{z} \\
\bar{f_{r}} \\
f_{z} \\
\bar{f_{r}} \\
f_{z} \\
\end{Bmatrix}\quad \bar{f}_{r}= \rho \bar{r} \omega^{2} \, \bar{r} = \frac{r_{i}+r_{j}+r_{m}}{3}
\end{align}
\]
\[
\begin{Bmatrix}
f_{s}
\end{Bmatrix} = \iint_{S}[\mathbf{N}]^{T}\begin{Bmatrix}
p_{r} \\
p_{z}
\end{Bmatrix}\mathrm{d}S = \frac{2\pi r_{j}(z_{m}-z_{j})}{2} \begin{Bmatrix}
0 \\
0 \\
p_{r} \\
p_{z} \\
p_{r} \\
p_{z}
\end{Bmatrix}
\]

