连续系统振动 I
弹性连续体振动
我们选取杆上 \(x\) 一小段截面 \(dx\) ，所以根据牛顿第二定律，我们有
\[
\sum F = m a
\]
对于这一截面，左右两侧的弹性力可由弹性力学的方式表示，即
\[
F(x,t) = A(x)\sigma(x,t) = A(x)E(x)\varepsilon(x,t)
\]
如果考虑外加的分布力 \(f(x,t)\) ，我们可以得到合力表示式
\[
\sum F= F(x+dx,t)-F(x,t)+f(x,y)
\]
由于
\[
ma = A(x)dx \rho(x)\frac{\partial^2 u }{\partial t^2}
\]
所以我们可以得到方程
\[
A(x)\rho(x) \frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}[E(x)A(x)\frac{\partial u}{\partial x}]+f(x,t)
\]
我们知道，一个振动系统方程在物理上可由力的方式描述，按照我们之前所学知识，上面三个表达式分别对应：惯性力、恢复力、激励。此时我们暂时不考虑阻尼影响，在连续体中，阻尼可分为两种：外阻和内阻（内阻一般与 \(E(x)\) 的表达式有关 ）。
对于杆的纵向振动，我们已经导出其振动方程
\[
\rho(x) A(x) \frac{\partial ^2u}{\partial t^2} - \frac{\partial}{\partial x}\left[E(x)A(x)\frac{\partial u}{\partial x}\right]=f(x,t)
\]
基于上述方程，类似地我们也可以导出弹性体振动
\[
\rho(x)I(x) \frac{\partial^2 \theta}{\partial t^2}-\frac{\partial}{\partial x}\left[G(x)I(x) \frac{\partial \theta}{\partial x}\right] = f(x,t)
\]
由材料力学中的知识可得，对于扭转问题，我们所关注的是扭矩 \(f\) 与转角 \(\theta\) 的关系。同时我们一般假设横截面在扭转振动中仍保持平面做整体转动，弹性力学告诉我们只有等截面圆轴才满足这一要求。
\[
\rho(x) A(x) \frac{\partial^2u}{\partial t^2}- \frac{\partial}{\partial x}\left[T(x)A(x)\frac{\partial u}{\partial x}\right] = f(x,t)
\]
在弦的振动问题中，\(A(x)\) 一般为变量，张力 \(T(x)\) 一般为常量。
我们一般采用分离变量法来求解上述方程。在数理方法中，对于上述的问题，一般需要给出初始条件和边界条件来构成定解问题。
\[
u(x,0) = \varphi(0),\frac{\partial u(x,0)}{\partial t}\Big|_{t=t_0} = \psi(0)
\]
固定：
\[
u(0,t) = 0
\]
自由：
\[
F(0,t)= 0
\]
弹性支撑：
\[
F(0,t) = k_1 u(0,t)
\]
集中质量：
\[
F(0,t) = - M\frac{\partial^2u}{\partial t^2}_{x=0}
\]
均匀弹性体
对于上述三种情况，当它们满足一定均匀性条件时，我们可以总结成如下波动方程
\[
\frac{\partial u}{\partial t^2}-c^2 \frac{\partial u^2}{\partial x^2}=0
\]
假定边界条件皆为两端固定 。我们知道可以通过分离变量方法来求解方程。
\[
u=X(x)T(t)
\]
取本征值 \(\lambda = -\omega^2\) ，根据边界条件我们知道本征值和其对于的本征函数
\[
\omega_i = \frac{ i\pi c}{L}
\]
\[
X_i =\sin \frac{\omega_{i}}{c}x
\]
在振动力学中，它们又被称为固有频率和振型，满足归一化条件。
时间函数满足
\[
T(t) = A \sin \omega_{i} t+B\cos \omega_{i}t
\]
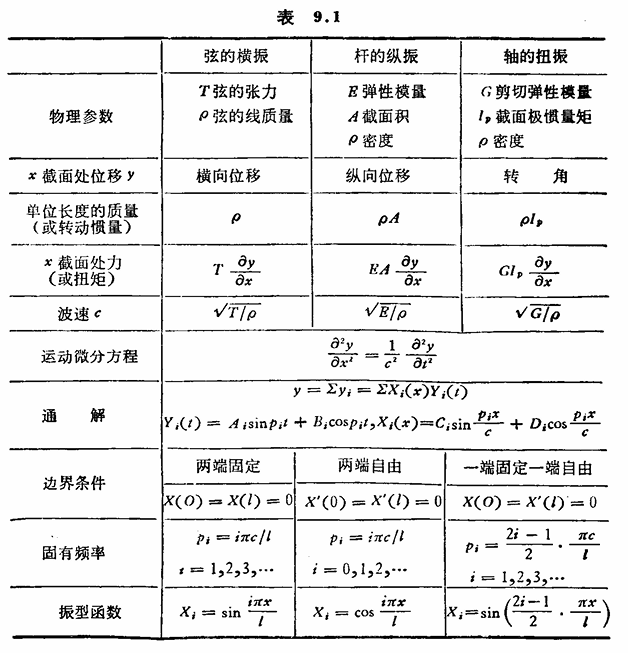
其他细节可参照下表：
非均匀弹性体及主振型叠加法
基于上述思想，我们依旧采用分离变量法来处理我们的振动问题。经过分离变量后，方程变形成如下形式：
\[
\frac{\ddot{T}(t)}{T(t)} = \frac{\frac{d}{dx}[E(x)A(x)\Phi'(x)]}{\rho(x)A(x)\Phi(x)} = -\omega^2
\]
于是固有频率及其对应的振幅应满足
\[
\frac{d}{dx}\left[E(x) A(x) \frac{d}{dx}\Phi_i(x)\right] =- \omega^2_i \rho(x)A(x)\Phi_i(x)
\]
正如前面的振动系统，我们研究其正交性。我们先给出结论
\[
\int_0^L\rho(x)A(x)\Phi_i(x)\Phi_j(x) = \left\{\begin{align}
0 \text{ i} \neq \text{j}\\
\overline{M}_i \text{ i} = \text{j}
\end{align} \right.
\]
\[
\int_0^L E(x)A(x)\Phi'_i(x)\Phi'_j(x) = \left\{\begin{align}
0 \text{ i} \neq \text{j}\\
\overline{K}_i \text{ i} = \text{j}
\end{align} \right.
\]
此时我们考虑的是两端固定、两端自由、一端固定和一端自由这三种边界情况。我们将上述这两种正交情况称为加权正交，它们分别表述振型函数所具有的正交性和其一阶导数所具有的正交性。
证明第一个方程：
考虑两个本征函数所满足的方程
\[
\begin{align}
\frac{d}{dx}\left[E(x) A(x) \frac{d}{dx}\Phi_i(x)\right] =- \omega^2_i \rho(x)A(x)\Phi_i(x)\\
\frac{d}{dx}\left[E(x) A(x) \frac{d}{dx}\Phi_j(x)\right] =- \omega^2_j \rho(x)A(x)\Phi_j(x)
\end{align}
\]
我们对第一式子做乘以 \(\Phi_j(x)\) 处理，然后在 \([0,L]\) 上积分
\[
\begin{align}
\int^L_0 \Phi_j(x)\frac{d}{dx}\left[E(x) A(x) \frac{d}{dx}\Phi_i(x)\right]dx =- \omega^2_i \int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx
\end{align}
\]
左式有分步积分展开得
\[
\left\{\Phi_j(x)\left[E(x)A(x) \frac{d}{dx} \Phi_i(x)\right]\right\}\Bigg|^L_0 - \int^L_0\Phi'_j(x) E(x)A(x)\Phi'_i(x)dx
\]
边界条件给出第一项为零，所以简化成
\[
\int^L_0\Phi'_j(x) E(x)A(x)\Phi'_i(x)dx =\omega^2_i \int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx
\]
同理可得，对于第二个本征函数所满足的方程有
\[
\int^L_0\Phi'_i(x) E(x)A(x)\Phi'_j(x)dx =\omega^2_j \int^L_0\Phi_i(x)\rho(x)A(x)\Phi_j(x)dx
\]
两式相减
\[
(\omega^2_i-\omega_j^2) \int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx=0
\]
由于 \(\omega_i\neq \omega_j\) ，所以
\[
\int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx=0
\]
也就是关于权重 \(\rho(x)A(x)\) 正交
第二个式子利用上述正交性由
\[\begin{align}
&\left\{\Phi_j(x)\left[E(x)A(x) \frac{d}{dx} \Phi_i(x)\right]\right\}\Bigg|^L_0 - \int^L_0\Phi'_j(x) E(x)A(x)\Phi'_i(x)dx \\&=- \omega^2_i \int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx
\end{align}
\]
得出。这边做一个简要描述：分布积分结果为零，所以等式左边第二项，也就是关于一阶导数的正交性只和等式右边也就是关于振型函数的正交性有关。
现在考虑边界条件为弹性支撑或者集中质量时的正交性条件，我们无法得出分部积分为零的结果，所以需要对原有的正交性进行修正。直接给出结论：
对于弹性支撑：
\[
\int_0^L E(x)A(x)\Phi'_i(x)\Phi'_j(x) dx+ k_1\Phi_i(0)\Phi_j(0)+k_2 \Phi_i(L)\Phi_j(L)= \left\{\begin{align}
0 \text{ i} \neq \text{j}\\
\overline{K}_i \text{ i} = \text{j}
\end{align} \right.
\]
对于集中质量：
\[
\int_0^L \rho(x)A(x)\Phi'_i(x)\Phi'_j(x) dx+ M_1\Phi_i(0)\Phi_j(0)+M_2 \Phi_i(L)\Phi_j(L)= \left\{\begin{align}
0 \text{ i} \neq \text{j}\\
\overline{M}_i \text{ i} = \text{j}
\end{align} \right.
\]
我们用一个复杂情况证明上述两个正交性：左端为弹性支撑、右端为集中质量。也就是
\[
\begin{align}
&\left[E(x)A(x)\frac{\partial u}{\partial x}\right]_{x=0}=k_1u(0,t)\\
&\left[E(x)A(x)\frac{\partial u}{\partial x}\right]_{x=L}=-M \frac{\partial^2}{\partial t^2} u(L,t)
\end{align}
\]
重复之前的步骤，我们依旧可以的得到在 \(0\sim L\) 上积分的关系式：
\[
\begin{align}
&\left\{\Phi_j(x)\left[E(x)A(x) \frac{d}{dx} \Phi_i(x)\right]\right\}\Bigg|^L_0 - \int^L_0\Phi'_j(x) E(x)A(x)\Phi'_i(x)dx \\&=- \omega^2_i \int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx
\end{align}
\]
我们对边界条件做一些处理，将 \(u = \sum \Phi_i(x) q_i(t)\) 带到边界条件中，利用 \(\ddot{q}_i(t) = -\omega^2_i q_i(t)\) 可得
\[
\begin{align}
&\left[E(x)A(x)\frac{d \Phi_i}{d x}\right]_{x=0}=k_1\Phi_i(0)\\
&\left[E(x)A(x)\frac{d \Phi_i}{d x}\right]_{x=L}=M \omega_i^2 \Phi_i(L)
\end{align}
\]
于是，在分部积分可展开成
\[
\left\{\Phi_j(x)\left[E(x)A(x) \frac{d}{dx} \Phi_i(x)\right]\right\} \Bigg|^L_0 = M \omega^2_i\Phi_i(L)\Phi_j(L)-k_1\Phi_i(0)\Phi_j(0)
\]
对另一个积分也做如上展开，然后两式相减可得
\[
(\omega^2_i-\omega_j^2) \left[\int^L_0\Phi_j(x)\rho(x)A(x)\Phi_i(x)dx+M \Phi_i(L)\Phi_j(L)\right ]=0
\]
可证明带有集中质量的正交性，对于弹性支撑的正交性可利用上述正交性仿照前文证得。
我们将振动方程简写成线性算子情况：
\[
L[u] = f(x,t)
\]
根据分量变量法，我们知道振动函数可以分解为时间函数和空间函数的叠加
\[
u(x,t) = \sum^{\infty}_{i=1} q_i(t)\Phi_i(x)
\]
我们可以利用之前导出的正交性对方程进行解耦。
\[
\int^L_0 \Phi_i(x) L[u] dx= \int^L_0 f(x,t)\Phi_i(x)dx
\]
假定 \(f(x,t) = p(x)F(t)\) 是可分离的，可得
\[
\overline{M}_i \ddot{q}_j(t) +\overline{K}_i q(t) ={\mathscr{F}_{i}}F_{}(t)
\]
其中 \(\mathscr{F} = \int^{l}_{0}p(x)\Phi(x)dx\) , 除以 \(\overline{M}_{i}\) 可将方程简化为
\[
\ddot{q}_{i} (t) + \omega^2_{i}q(t) = \frac{\mathscr{F}_{i}}{\overline{M}_{i}}F_{}(t)
\]
同时我们对于初始条件进行处理
\[
\begin{align}
&q_i(0) = {\int^L_0 \rho(x)A(x)\varphi(x) \Phi_i(x) \over\overline{M}_i}\\
&\dot{q}_i(0) = {\int^{L}_{0}\rho(x) A(x)\psi(x) \Phi_j(x)\over \overline{M}_i}
\end{align}
\]
通过求解上述二次微分方程，就可以确定时间函数，我们采用杜哈梅积分可得
\[
q_{i}(t) = q_{i}(0) \cos \omega_{i }+\frac{1}{\omega_{i}}\dot{q}_{i}(0 ) \sin \omega_{i}+\frac{\mathscr{F}_{i}}{\overline{M}_{i}\omega_{i}}\int^{t}_{0}F(\xi)\sin \omega_{i}(t-\xi)d\xi
\]
将其叠加就得到我们想要的结果
梁的弯曲振动问题
回忆我们在材料力学对于杆弯曲所做的假设，现在我们假定梁未变形时各截面形心的连线是直线，假设梁具有对称平面，且在弯曲振动中的轴线始终保持在一对称平面内。
所以，梁的弯曲振动可表示为
\[
w(x,t)
\]
根据材料力学理论，我们可以列出描述梁弯曲振动的表达式：
挠曲线： \(w(x,t)\)
转角：\(\theta = \frac{\partial w}{\partial x}\)
弯矩： \(M(x,t) = E(x)I(x)\frac{\partial^2 w}{\partial^2 x}\)
剪力：\(P(x,t) = \frac{\partial M}{\partial x}\)
分布力：\(f(x,t) =\frac{\partial P}{\partial x}\)
通过达朗贝尔原理，可以导出描述梁振动的方程：
\[
\frac{\partial^2}{\partial x^2}[E(x)I(x)\frac{\partial^2}{\partial x^2}w] + \rho(x)A(x) \frac{\partial^2 w}{\partial t^2} = f(x,t)
\]
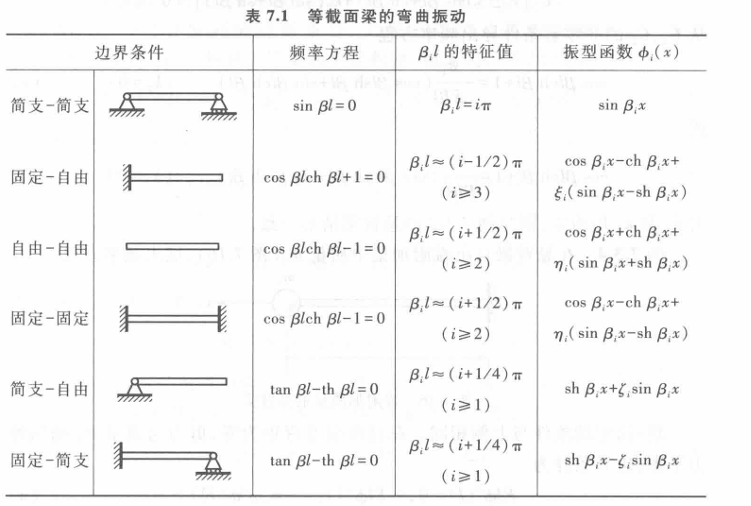
梁弯曲振动的边界条件和之前讨论的类似，常见的边界条件有：
固支端 ：挠度和转角都为零
\[
w(x_0,t) = 0,\quad \theta(x_0,t)=0
\]
简支端 ：挠度和弯矩都为零
\[
w(x_0,t) = 0 \quad M(x_0,t) = 0
\]
自由端 ：弯矩和剪力都为零
\[
M(x_0,t) =0 \quad P(x_0,t) =0
\]
夹支端 ：转角和剪力都为零
\[
\theta (x_0,t) =0 \quad P(x_0,t)=0
\]
弹性支撑 ：弹性支撑有两种，一种是影响剪力的弹簧，一种是影响弯矩的扭簧
\[
M(x_0,t) = k_1 \theta_1(x_0,t) \quad P(x_0,t)= k_2 w(x_0,t)
\]
集中质量 ：集中质量只影响剪力，不影响弯矩
\[
P(x_0,t) = M \frac{\partial^2 w}{\partial t^2}\quad M(x_0,t) =0
\]
Notes
我们引入了四个物理量描述杆的振动，所以两两组合理论上可以给出 6 种边界条件组合，但实际上只有四种，这是因为 弯矩和转角、力和位移 在物理上被称为是对偶量
同样的，我们采用分离变量法来求解这个四阶偏微分方程。取
\[
w(x,y)=\Phi(x)T(t)
\]
现在只考虑常系数方程以及没有外加激励，所以对于振型函数有：
\[
\frac{d^4 \Phi}{d x^4}-\beta^4\Phi =0\quad \beta^2 \equiv \frac{\rho A}{EI}\omega^2
\]
这是一个四阶常系数线性常微分方程，它的特征方程为
\[
\lambda^4 -\beta^4 =0
\]
对应特征根为
\[
\lambda_{1} =\beta \quad \lambda_{2}=-\beta \quad \lambda_{3}=i\beta \quad\lambda=-i\beta
\]
所以常微分方程的通解为
\[
\Phi(x)= C_1\cosh \beta x +C_{2}\sinh \beta x+C_{3}\cos \beta x+C_{4}\sin \beta x
\]
我们可以利用边界条件确定任意常数的相对比值和频率方程来导出固有频率和振型函数。我们将边界条件中要用到的 \(\Phi(x)\) 的各阶导数列出如下：
\[
\begin{align*}
&\Phi'(x) = \beta[ C_1\cosh \beta x +C_{2}\sinh \beta x-C_{3}\sin \beta x+C_{4}\cos \beta x]\\
&\Phi''(x)=\beta^2[ C_1\cosh \beta x +C_{2}\sinh \beta x-C_{3}\cos\beta x-C_{4}\sin \beta x]\\
&\Phi''(x) = \beta^3[ C_1\cosh \beta x +C_{2}\sinh \beta x+C_{3}\sin \beta x-C_{4}\cos \beta x]
\end{align*}
\]
（注：对于 \(X=0\) 的边界条件，可以导出四个任意常数之间的关系； 对于 \(X=L\) 的边界条件，利用行列式为零）
正交性问题
梁的弯曲振动：
\[
\frac{\partial^2}{\partial x^2}[E(x)I(x)\frac{\partial^2}{\partial x^2}w] + \rho(x)A(x) \frac{\partial^2 w}{\partial t^2} = f(x,t)
\]
同样的，我们采用分离变量法来求解上述方程，取
\[
w(x,t) = \Phi(x)T(t)
\]
所以方程变为
\[
\begin{align}
&\ddot{T}(t) +\omega^{2}T(t) = 0\\ \\
&\frac{d^{2}}{dx^{2}}\left[ E(x)I(x) \frac{d^{2}\Phi(x)}{dx^{2}} \right] =\omega^{2} \rho(x) A(x)\Phi(x)
\end{align}
\]
数学上能证明上述方程具有离散解 \(q_{i}(t),\Phi_{i}(x)\) 。如果考虑固支、简支、自由、夹支这四种边界条件，同样有正交性：
\[
\int^{L}_{0}\rho(x)A(x)\Phi_{i}(x)\Phi_{j}(x) = \begin{cases}
\overline{M}_{i} &i =j\\
0 &i \neq j
\end{cases}
\]
\[
\int^{L}_{0}E(x)A(x) \Phi''_{i}(x)\Phi''_{j}(x) = \begin{cases}
\overline{K}_{i} &i=j\\
0& i\neq j
\end{cases}
\]
证明如下：
左乘 \(\Phi_{j}(x)\) 并作积分
\[
\int^{L}_{0}\Phi_{j}(x)\frac{d^{2}}{dx^{2}}\left[ E(x)I(x) \frac{d^{2}}{dx^{2}}\Phi_{i}(x) \right]dx =\omega_{i}^{2} \int_{0}^{L} \, \rho(x) A(x)\Phi_{i}(x)\Phi_{j}(x)
\]
做两次分步积分可得
\[\begin{align}
&\int^{L}_{0}\Phi_{j}(x)\frac{d^{2}}{dx^{2}}\left[ E(x)I(x) \frac{d^{2}}{dx^{2}}\Phi_{i}(x) \right]dx = \Phi_{j}(x)\frac{d}{dx}\left[ E(x)I(x)\Phi''_{i}(x) \right]\Big|^{L}_{0} \\
&\qquad- \Phi'_{j}(x)E(x) I(x)\Phi''(x)\Big|^{L}_{0}+ \int_{0}^{L} \Phi''(x)\Phi''(x)E(x)I(x)dx \,
\end{align}
\]
这边简要描述边界条件的对应关系
\[
\begin{align}
w(x_{0},t) =0 &\Rightarrow \Phi(x_{0}) =0 \\ \\
\theta(x_{0},t) =0 &\Rightarrow \Phi'(x_{0}) =0 \\ \\
M(x_{0},t) =0 &\Rightarrow E(x_{0})I(x_{0})\Phi''(x_{0}) =0 \\ \\
P(x_{0},t) =0 &\Rightarrow \frac{ d}{dx}[E(x_{0})I(x_{0})\Phi''(x_{0})] =0
\end{align}
\]
代入上式可得
\[
\int^{L}_{0}\Phi_{j}(x)\frac{d^{2}}{dx^{2}}\left[ E(x)I(x) \frac{d^{2}}{dx^{2}}\Phi_{i}(x) \right]dx = \int_{0}^{L} \Phi''(x)\Phi''(x)E(x)I(x)dx
\]
也就是
\[
\int_{0}^{L} \Phi''(x)\Phi''(x)E(x)I(x)dx =\omega_{i}^{2} \int_{0}^{L} \, \rho(x) A(x)\Phi_{i}(x)\Phi_{j}(x)
\]
再取一个振型 \(\Phi_{j}(x)\) 便可以证明正交性。
Notes
上述可以说明为什么边界条件不能出现 \(w,P\) 和\(\theta,M\) 这两种组合，就是因为无法保证分部积分中的两个积分项同时等于零
同样的，可以得到边界条件为弹性支撑和集中质量的正交性
\[
\begin{align}
&P(0,t)= -k_1 w(0,t) \ \ \ \quad M(0,t) = k_2 \theta(0,t) \\
&P(L,t)= k_3 w(L,t) \quad M(L,t) = -k_4 \theta(L,t)
\end{align}
\]
对应关于刚度的正交性
\[
\begin{align}
&\int^{L}_{0}E(x)A(x) \Phi''_{i}(x)\Phi''_{j}(x) \,dx+ k_{1}\Phi_{i}(0)\Phi_{j}(0)+k_{2}\Phi'_{i}(0)\Phi'_{j}(0) \\
&\qquad+ k_{3}\Phi_{i}(L)\Phi_{j}(L)+k_{4}\Phi'_{i}(L)\Phi'_{j}(L)= \begin{cases}
\overline{K}_{i} &i=j\\
0& i\neq j
\end{cases}
\end{align}
\]
\[
\begin{align}
&w(0,t) =0 \qquad \qquad \quad \theta(0,t) =0 \\
&P(L,t) = -M \frac{\partial^2 w}{\partial t^2}\quad M(L,t) =0
\end{align}
\]
对应关于质量的正交性
\[
\int^{L}_{0}\rho(x)A(x)\Phi_{i}(x)\Phi_{j}(x) +M_{0}\Phi(L)\Phi(L)= \begin{cases}
\overline{M}_{i} &i =j\\
0 &i \neq j
\end{cases}
\]
Notes
对于上述两种特殊的边界条件，我们在一开始讨论的时候并没有讨论其正负号，因为这个和坐标选定有关，但是无论如何，其边界条件必须满足上述正交性中的修正项为正，也就是取 “+”（考虑能量）
特殊问题
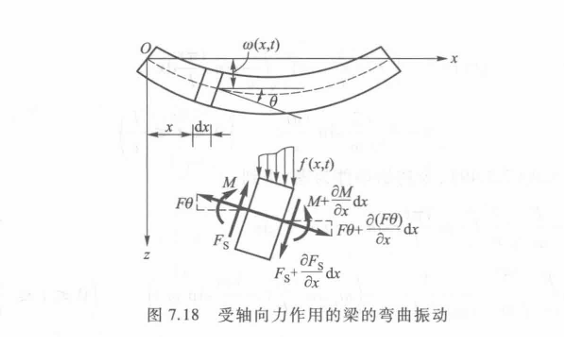
轴向力对梁弯曲振动的影响
如果各截面存在常值轴向拉力 \(F\) 和 \(-F\) ，列写力平衡方程时应增加此轴向力沿 \(z\) 方向的分量，方程改写为
\[
\rho(x)A(x) dx \frac{\partial ^{2}w}{\partial t^{2}} = \left( F_{s}+\frac{\partial F_{s}}{\partial x}dx \right) -F_{s}+\left( F \theta +\frac{\partial (F \theta) }{\partial x}dx \right) - F \theta +f(x,t)dx
\]
(这里设轴向拉力在 \(x\) 方向的作用 \(F \sin \theta \approx F \theta\) )
利用之前的结论，可得受轴向力作用梁的弯曲振动方程：
\[
\frac{\partial^{2}}{\partial x^{2}}\left[ E(x)I(x) \frac{\partial^{2} w(x,t)}{\partial x^{2}}\right] + \rho(x)A(x) \frac{\partial^{2} w(x,t)}{\partial x^{2}} -F \frac{\partial^{2}w(x,t)}{\partial x^{2}} = f(x,t) \tag{1}
\]
考虑均匀梁。分离变量结果：
\[
\begin{align}
\ddot{T}(t) + &\omega^{2} T(t)=0 \\
\frac{d^{4}\Phi(x)}{dx^{4}} - \frac{F}{EI} \frac{d^{2 }\Phi(x)}{dx^{2}}&-\frac{\rho A}{EI}\omega^{2}\Phi(x)=0
\end{align}
\]
特征方程 \(\lambda^{4} - \delta^{2}\lambda^{2}-\beta^{4}=0\) 的根：
\[
\lambda_{1}= \text{i}\beta_{1} \quad\lambda_{2} =-\text{i}\beta_{1}\quad \lambda_{3} = \beta_{2} \quad\lambda_{4}=- \beta_{2}
\]
其中
\[ \begin{align}
\beta_{1} = \sqrt{ \sqrt{ \frac{\rho A}{EI}\omega^{2}+\left( \frac{F}{2EI} \right)^{2} }-\frac{F}{2EI}}\qquad\beta_{2} = \sqrt{ \sqrt{ \frac{\rho A}{EI}\omega^{2}+\left( \frac{F}{2EI} \right)^{2} }+\frac{F}{2EI}}
\end{align}
\]
所以方程通解
\[
\phi(x) = \cos \beta_{1} x+\sin \beta_{1}x+\cosh \beta_{2}x+\sinh \beta_{2}x
\]
看一个🌰：
\[
\sin \beta_{1}l =0
\]
解出
\[
\beta_{1i}l = \text{i} \pi
\]
固有频率：
\[
\omega^{2}_{i} = \left( \frac{\text{i}\pi}{l} \right) ^{2}\sqrt{ \frac{EI}{\rho A}\left[ 1+\frac{F}{EI}\left( \frac{l}{\text{i}\pi}\ \right) ^{2}\right] }
\]
如果 \(F\) 为正（受拉也就是图上所示方向），则固有频率提升，从物理上理解是系统的等效刚度变大（考虑 \(\omega^{2} = \frac{\bar{K}}{\bar{M}}\) ），\(F\) 为负（受压）则是等效刚度减小
当杆受压时，为了确保固有频率有实数解，\(\lvert F \rvert\) 需要小于一个临界值 \(\lvert F \rvert_{\text{cr}}\)
\[
\lvert F \rvert _{cr}=\frac{(\text{i}\pi)^{2}EI}{l^{2}}
\]
此临界为材料力学压杆的欧拉载荷。
Timoshenko 梁的自由振动
对于较短粗的梁，需要考虑剪切变形和转动惯量的影响，也就是 Timoshenko 梁问题。因为截面存在剪切变形，起法线轴与中心轴的切线就不再保持一致，记梁的的切变模量为 \(G\) ，剪力 \(F_{s}\) 作用下产生的切应变 \(\gamma\) 为
\[
\gamma = \frac{F_{s}}{\kappa GA}
\]
\(\kappa\) 为截面形状因素，切应变导致中心轴切线偏转，则
\[
\frac{\partial w}{\partial x} = \theta + \gamma
\]
考虑自由振动问题，即无外加激励，达朗贝尔原理给出沿 \(z\) 轴的力平衡方程
\[
\kappa GA \frac{\partial }{\partial x}\left( \frac{\partial w}{\partial x} - \theta \right) - \rho A \frac{\partial^{2}w}{\partial t^{2}}= -f(x,t)=0 \tag{2}
\]
截面转动时产生惯性力矩 \(-\rho I \frac{\partial^{2} \theta}{\partial t^{2}}\) ，考虑力矩平衡
\[
\frac{\partial M}{\partial x}-F_{s }+\rho I\frac{\partial^{2} \theta}{\partial t^{2}}=0
\]
用 \(w\) 和 \(\theta\) 表示得
\[
EI \frac{\partial^{2}\theta}{\partial x^{2}}+\kappa GA\left( \frac{\partial w}{\partial x}-\theta \right) - \rho I \frac{\partial^{2 }\theta}{\partial t^{2}}=0 \tag{3}
\]
对 \(x\) 做偏导得
\[
EI \frac{\partial^{3}\theta}{\partial x^{3}}+\kappa GA\frac{\partial }{\partial x}\left( \frac{\partial w}{\partial x}-\theta \right) - \rho I \frac{\partial^{2}}{\partial t^{2}}\left( \frac{\partial \theta}{\partial x} \right) =0 \tag{4}
\]
\((2)\) 式给出
\[
\frac{\partial \theta}{\partial x} = \frac{\partial^{2}w}{\partial x^{2}}-\frac{\rho}{\kappa G} \frac{\partial^{2} w}{\partial t^{2}}
\]
将上式带入 \((4)\) 式中可得Timoshenko 梁自由振动方程：
\[
EI \frac{\partial^{4}w}{\partial x^{4}}+\rho A \frac{\partial^{2} w}{\partial t^{2}} - \rho I\left( 1+\frac{E}{\kappa G} \right) \frac{\partial^{4}w}{\partial x^{2}\partial t ^{2}}+\frac{\rho I}{\kappa G}\frac{\partial^{4}w}{\partial t^{4}} =0
\]
如果忽略剪切变形，取 \(G \to \infty\) 则可简化为
\[
EI \frac{\partial^{4}w}{\partial x^{4}} +\rho A \frac{\partial w^{2}}{\partial t^{2}}- \rho I \frac{\partial^{4}w}{\partial x^{2}\partial t ^{2}}=0
\]
分离变量：
\[
\begin{align}
\ddot{T}(t) +&\omega^{2} T(t) =0 \\
\frac{d^{4}\Phi(x)}{dx^{4}}+\omega^{2}\frac{\rho}{E} &\frac{d^{2}\Phi(x)}{dx^{2}}-\omega^{2}\frac{\rho S}{EI}\Phi(x) = 0
\end{align}
\]
如果考虑剪切变形的影响，忽略惯性力矩，则振动方程可简化为
\[
EI \frac{\partial^{4}w}{\partial x^{4}} +\rho A \frac{\partial^{2}w}{\partial t^{2}}-\left( \frac{\rho EI}{\kappa G} \right) \frac{\partial^{4}\omega}{\partial x^{2}\partial t^{2}}=0
\]
含结构阻尼梁的弯曲振动
如果材料在变形过程中存在由内摩擦引起的结构阻尼，所以动应力可以表示为
\[
\sigma(x,t) =E \left[ \varepsilon(x,t)+\eta \frac{\partial \varepsilon(x,t)}{\partial t} \right]
\]
所以弯矩改成
\[
M=EI \left( \frac{\partial^{2}w}{\partial x^{2}}+\eta \frac{\partial^{3}w}{\partial^{2}x \partial t} \right)
\]
所以弯曲振动方程可以改为
\[
EI\frac{\partial ^{4}(x,t)}{\partial x^{4}}+\eta EI\frac{\partial^{5}w(x,t)}{\partial x^{4 }\partial t}+ \rho A \frac{\partial^{2} \omega(x,t)}{\partial t^{2}}=f(x,t)
\]
取保守系统的线性组合 \(w(x,t)=\sum^{\infty}_{i=1}\varphi_{i}(x)q_{i}(t)\) ，带入上述方程，并作如下积分处理(正交化)
\[
\int_{0}^{L}\varphi_{j}\left\{ EI\sum^{\infty}_{i=1}\varphi_{i}^{(4)}q_{i}+\eta EI\sum^{\infty}_{i=1}\varphi_{i}^{(4)}q_{i} +\rho A\sum^{\infty}_{i=1}\varphi_{i}\ddot{q}_{i}\right\} \,dx = \int_{0}^{L} \varphi_{j} {f(x,t)} \, dx
\]
根据保守的正交性条件，可得
\[
\ddot{q}_{j}(t) +\eta \omega^{2}_{j}\dot{q}_{j}(t) +\omega^{2}_{j}q_{j}(t) = \frac{f_{j}}{\overline{M}_{j}} \qquad \omega_{j} = \frac{\overline{K}_{j}}{\overline{M}_{j}}
\]
对于梁的弯曲振动，之前并没有考虑过阻尼作用。在多自由度振动系统中，我们提到过当存在阻尼影响时，方程可能无法解耦。因此在弯曲振动中，如果存在阻尼影响，我们也可能无法对方程解耦，上面是一种特殊情况。还有一种阻尼作用情况可以解耦，振动方程满足如下形式：
\[
\frac{\partial^2}{\partial x^2}\left[ E(x)I(x)\frac{\partial^2w}{\partial x^2} \right] +\beta_{1}\frac{\partial^2}{\partial x^2}\left[ E(x)I(x)\frac{\partial^2w}{\partial x^2} \right]+ \rho(x)A(x) \frac{\partial^2 w}{\partial t^2}+\beta_{2}\rho(x)A(x)\frac{\partial w}{\partial t} = f(x,t)
\]
这种情况其实是在多自由振动系统中讨论过的比例阻尼 \(C = \alpha M+ \beta K\) ，因对上述方程作正交化处理，阻尼就变成广义刚度和广义质量的线性组合。
膜和板的振动
薄膜横向振动：
\[
\rho h \frac{\partial^{2} w}{\partial t^{2}} - F \nabla^{2}w =0
\]
其中 \(\rho\) 为薄膜密度， \(h\) 为薄膜厚度，\(\nabla^{2} = \frac{\partial^{2} }{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\)
\[
\rho h \frac{\partial^{2} w}{\partial t^{2}}+D \nabla^{4 } \omega = f
\]
\(D\) 为抗弯刚度，满足
\[
D = \frac{Eh^{3}}{12(1-\nu^{2})}
\]
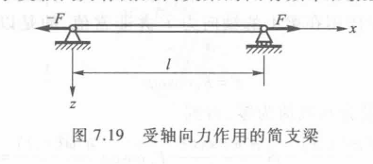考虑如上简支梁，根据边界条件可以解出频率方程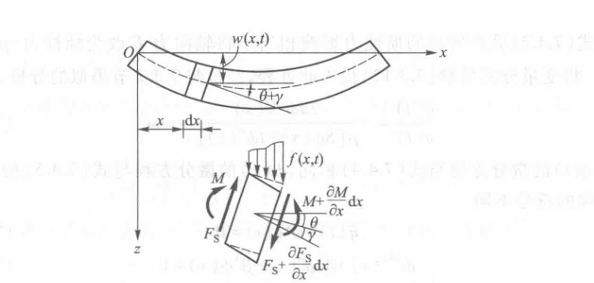
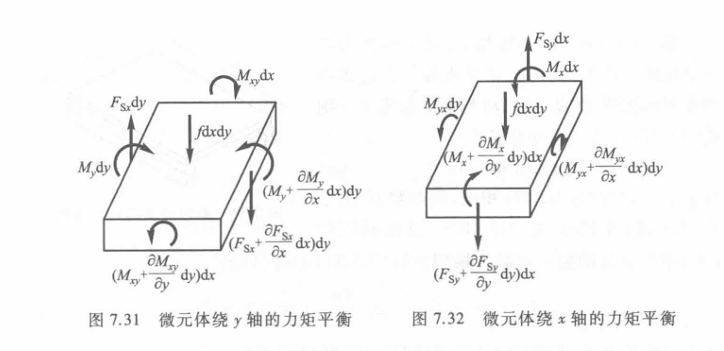板的振动