Linear Classifier

约 1578 个字 8 张图片 预计阅读时间 11 分钟

Linear Classifier

Algebraic Viewpoint

线性映射：

\[ f(x,W) = Wx+b \]

在上面的公式中，假设每个图像数据都被拉长为一个长度为D的列向量，大小为 \([D \times 1]\) 。其中大小为 \([K \times D]\) 的矩阵W和大小为 \([K \times 1]\) 列向量b为该函数的参数（parameters）。以上图猫猫为例， \(x_i\) 就包含了第i个图像的所有像素信息，这些信息被拉成为一个\([3072 \times 1]\) 的列向量，W大小为 \([10\times3072]\)，b的大小为 \([10\times1]\)。因此，3072个数字（原始像素数值）输入函数，函数输出10个数字（不同分类得到的分值）。参数W被称为权重（weights）。b被称为偏差向量（bias vector），这是因为它影响输出数值，但是并不和原始数据 \(x_i\) 产生关联。在实际情况中，人们常常混用权重和参数这两个术语。

线性分类器计算图像中3个颜色通道中所有像素的值与权值的矩阵乘，从而得到分类分值。根据我们对权重设置的值，对于图像的某些位置的某些颜色，函数表现出喜好或者厌恶

Visual Viewpoint

将线性分类器看做模板匹配：关于权重W的另一个解释是它的每一行对应着一个分类模板（模型）。一张图像对应不同分类的得分，是通过使用内积来比较图像和模板，然后找到和哪个模板最相似。

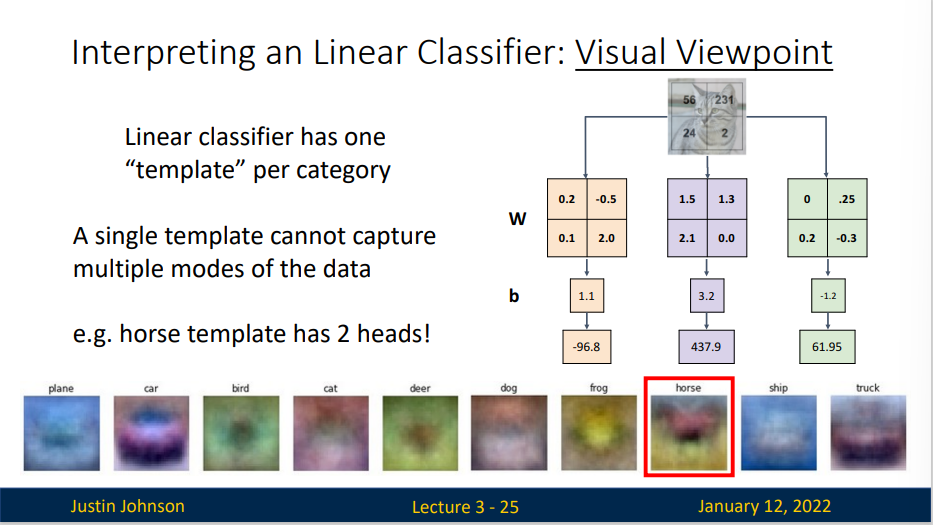
A single template cannot capture multiple modes of the data

可以看到马的模板看起来似乎是两个头的马，这是因为训练集中的马的图像中马头朝向各有左右造成的。线性分类器将这两种情况融合到一起了。类似的，汽车的模板看起来也是将几个不同的模型融合到了一个模板中，并以此来分辨不同方向不同颜色的汽车。

Geometric Viewpoint

选取图像上的一个像素点，用线性分类器计算这个像素点的得分来判断它更有可能是哪种图片的像素

我们扩展这个思想，将其运用到多个像素点的计算中，比如说选取两个像素点，计算这个两个像素点的得分，以其中一个像素点得分为X轴，另一个像素点得分为Y轴

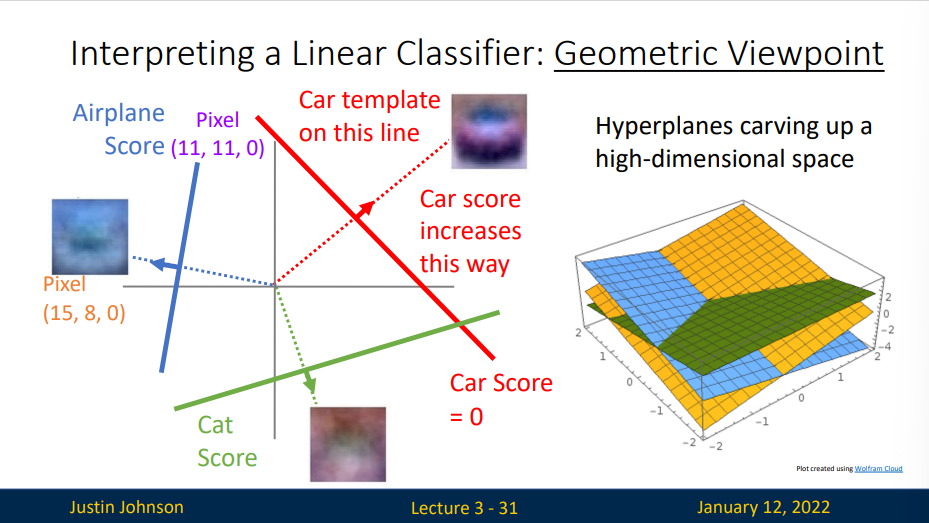
图像空间的示意图。其中每个图像是一个点，有3个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为0的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低。

对于这些数字的几何解释是：如果改变其中一行的数字，会看见分类器在空间中对应的直线开始向着不同方向旋转。而偏差b，则允许分类器对应的直线平移。需要注意的是，如果没有偏差，无论权重如何，在\(x_i = 0\)时分类分值始终为0。这样所有分类器的线都不得不穿过原点。

hyperplanes carving up a high-dimensional space

我们生活在三维（低维）世界，能够直观想象低维的数据的几何构型，但是并不能直观地想象高维数据的几何构型。

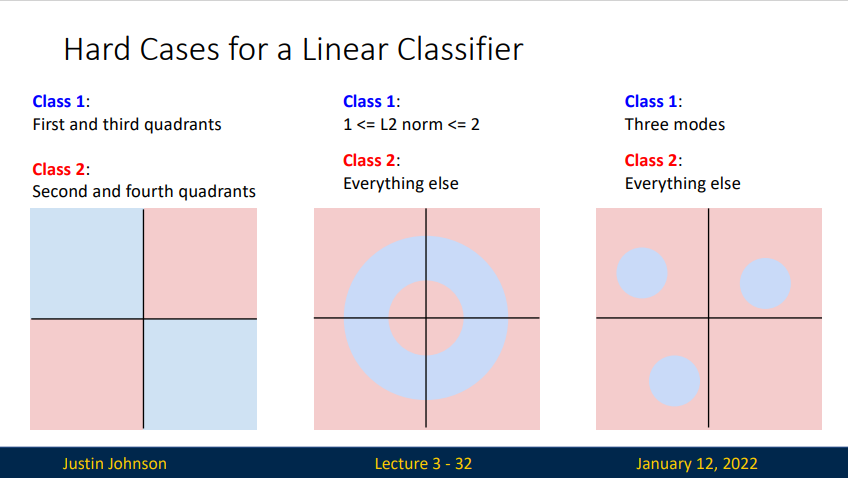
Hard case for linear classifier

Loss Function

A loss function or cost function (sometimes also called an error function)is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event.

• Low loss = good classifier
• High loss = bad classifier

当评分函数输出结果与真实结果之间差异越大，损失函数输出越大，反之越小。

Loss for the dataset is average of per-example losses:

\[ L = \frac{1}{N}\sum_iL_i(f(x_i,W),y_i) \]

Cross-Entropy Loss (Multinomial Logistic Regression)

熵表示热力学系统的无序程度，在信息学中可以表示信息的无序程度，在图像分类中，真实标签向量只有一个元素为1，这种情况无序程度最低，这也是我们期望模型输出可以达到的程度

交叉熵损失可以衡量两个向量之间的差异程度，并且只关心正确分类的问题，不会去关心错误分类的概率，可以使得模型更专注于强化正确分类的概率

We interpret raw classifier scores as probabilities:

\[\begin{align} &s = f(x_i;W)\\ &P(Y = k|X =x_i)=\frac{\text{exp}(s_k)}{\Sigma_j\text{exp}(s_j)}\quad \text{Softmax function}\\ &L_i=-\log P(Y=y_i|X=x_i) \\ &D_{KL}(P||Q) = \sum_yP(y)\log \frac{P(y)}{Q(y)} \end{align} \]

在Softmax分类器中，函数映射 \(f(x_i,W) = W x_i\) 保持不变，其输出是线性分类器预测的原始分数，但将这些评分值视为每个分类的未归一化的对数概率（或者叫做非标准化的对数概率），进行指数计算之后，所有的分数转化为正数，并且将折叶损失（hinge loss）替换为交叉熵损失(cross-entropy loss)。

\(f_j(z) = \frac{e^{z_j}}{\sum_ke^{z_k}}\) 称为softmax 函数：其输入值是一个向量，向量中元素为任意实数的评分值（\(z\)中的），函数对其进行压缩，输出一个向量，其中每个元素值在0到1之间，且所有元素之和为1。

Multiclass SVM Loss

The score of the correct class should be higher than all the other scores

SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值Delta。

如果第 \(i\) 个数据中包含图像 \(x_i\) 的像素和代表正确类别的标签 \(y_i\) 评分函数输入像素数据,然后通过公式 \(f(x_i,W)\) 来计算不同分类类别的分值。于是，针对第i个数据的多类SVM的损失函数定义如下:

\[ L_i = \sum_{j\neq _i}\max (0,s_j-s_{y_i}+\Delta) \]

\(\max(0,-)\) 函数被称为折叶损失（hinge loss）。\(\max(0,-)^2\) 则被称为平方折叶损失（L2-SVM）,它将更强烈的惩罚过界的边界值。

Summary