Supervised Learning of Behaviors

约 2018 个字 5 张图片 预计阅读时间 13 分钟

Terminology & notation

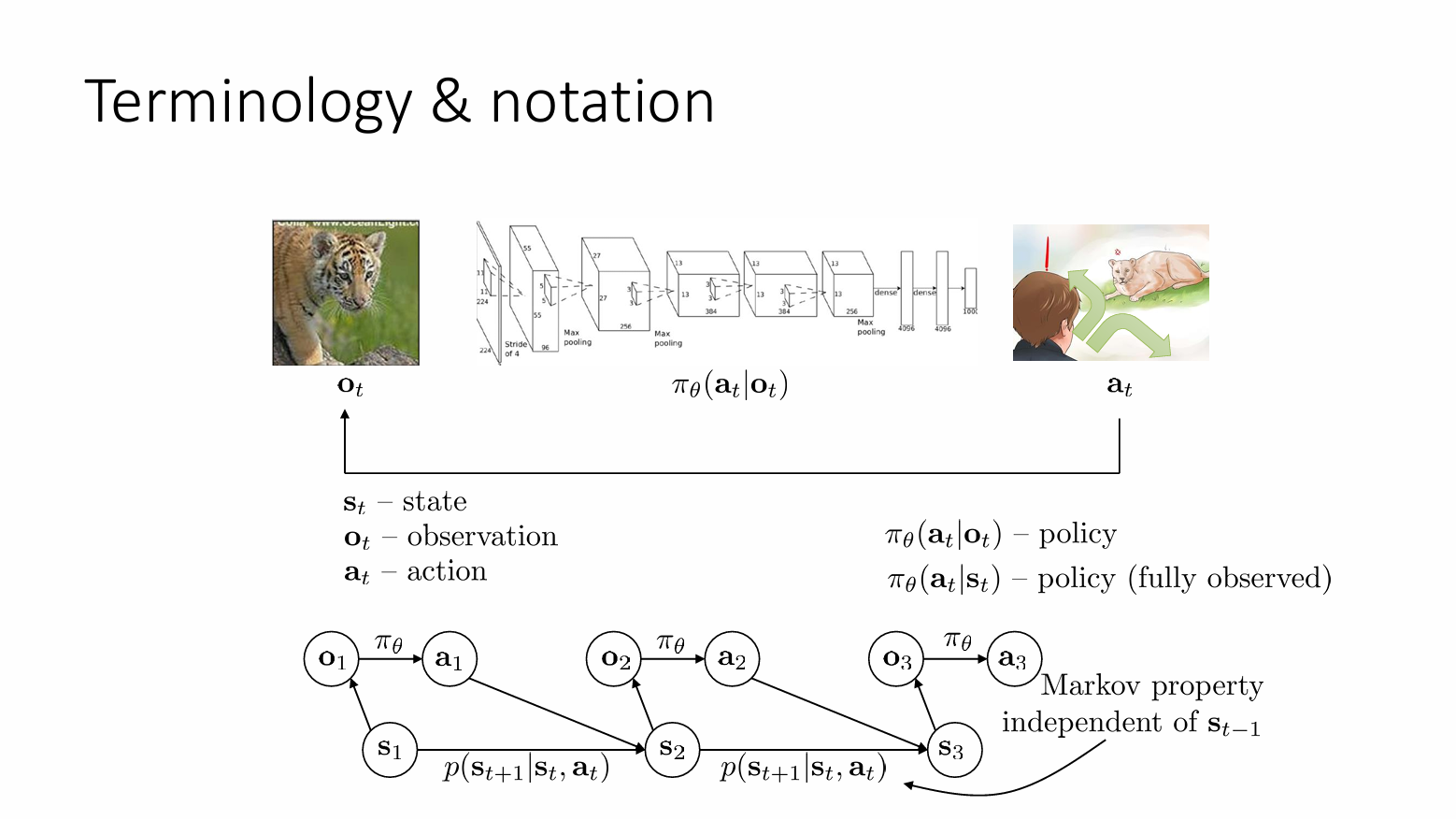
• State：状态 \(S_{t}\)
• Observation：观察 \(O_{t}\)
• Action：动作 \(a_{t}\)
• Policy：策略 \(\pi_{\theta}(a_{t}|o_{t})\)

动作空间可以是离散的，比如说在自动驾驶中，我们输出向前、向左、向右的信号；当然也可以是连续的，比如说高斯分布，但是我们输出的时候连续分布的相关参数，比如说均值、协方差。

策略（Policy）表示在给定 \(o_{t}\) 时 \(a_{t}\) 的分布，策略有些时候输出的是可能的动作分布，这时候我们选取最佳数据，也可能输出一个确定性的特例，此时只是将概率 \(1\) 赋予这个确定性的特例，而将其他动作的概率赋予 \(0\) 。

注意上图给出了两种策略，一种是基于 Observation 的 policy ，一种是基于 State 的 policy。State 和 Observation 并不是一样的。比如说输入一个豹子在追鹿的图片，此时这张图片是 Observation，如果此时图片中的豹子被遮挡，那就不一定会输出豹子在追鹿这件事，但是 State 并不会受影响，也就是说 State 是一个对客观事物简洁完整的描述。

再比如说，在自动驾驶中，Observation 可能只包括车辆的传感器捕捉到的前方和侧面的交通情况，而忽略了后方的情况。于是如果后方发生某些影响到车辆的事情，此时的 State 发生了变化，但是 Observation 可能并不会发生什么变化。

在理想状态下，State 是一个Markov状态，这意味着当前的状态包含了足够的信息以预测未来，而不需要参考过去的历史。换句话说，在一个完全可观察的环境中，如果智能体能够访问环境的确切状态，那么它就拥有了一个全局视角，即所谓的“上帝视角”，这使得它能够基于完整的环境信息来做出最优决策。

Warning

Observation 和 State 经常被搞混

在控制中，也可以用 \(x_{t}\) 表示状态，\(u_{t}\) 表示动作

Imitation Learning

部分笔记内容参考：模仿学习(Imitation Learning)入门指南

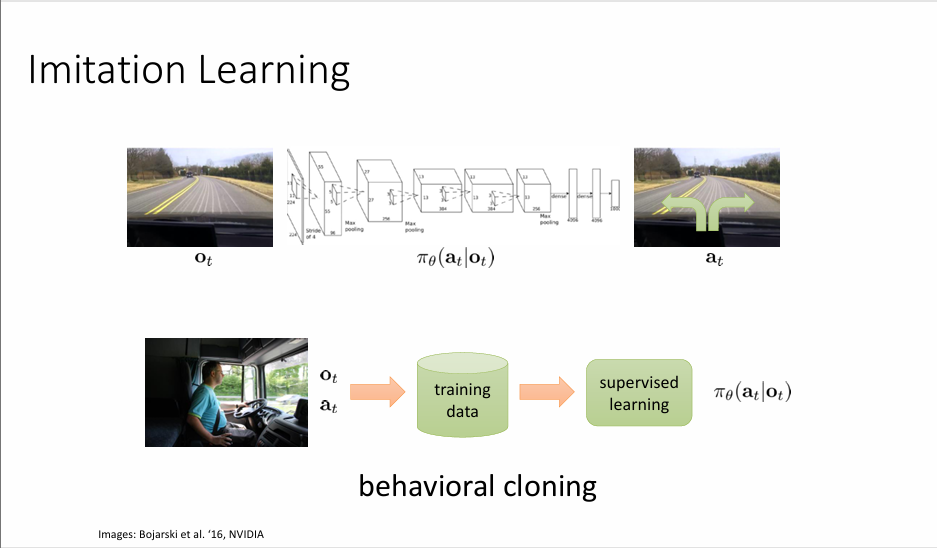
Imitiation Learning 的想法是，借助人类给出的示范(demonstration)，可以快速地达到这个目的。以自动驾驶为例，\(o_{t}\) 是摄像头拍下的道路情况，\(a_{t}\) 是方向盘的行为，比如说左转、右转，这个构成了一个数据集。我们希望训练出来的模型是模型生成的状态-动作轨迹分布 \(p_{\pi_{\theta}}(o_{t})\) 和输入的轨迹分布 \(p_{\text{data}}(o_{t})\) 向匹配。在自动驾驶中就是模型会根据摄像头拍到的道路情况做出左转或者右转的决策。我们把这种行为称为行为克隆(Behavior Cloning)

ALVINN: An Autonomous Land Vehicle in a Neural Network

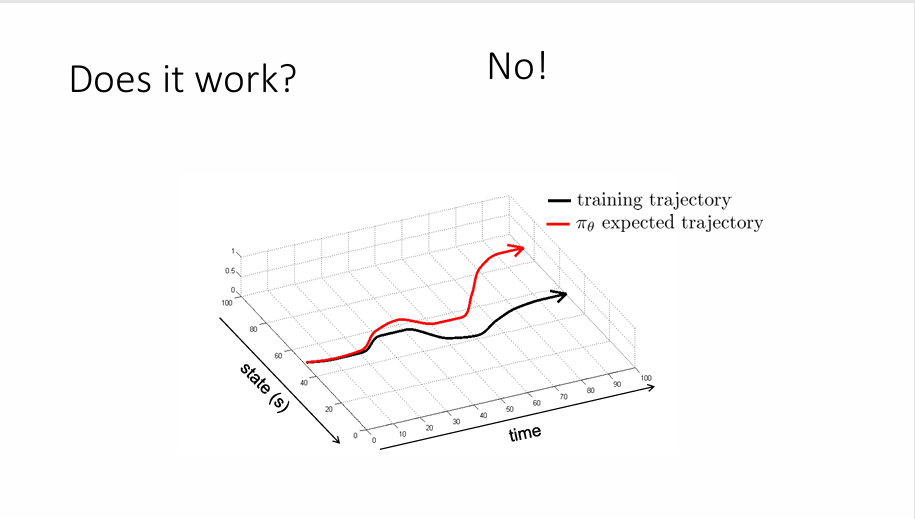
但是，这种方法并不一定能起作用。上图黑色的路线是训练数据的路线，我们希望模型做出的路线（红色）能和黑色一样，但是显然并没有。原因很简单，对于模型而言，在时间推进过程中，它有一定概率会犯错误，尽管这些错误很微小，但是对于模型而言来说可能是致命的，因为它进了一个“陌生”的道路，他没有办法根据训练结果做出反馈，于是更有可能犯下错误，而这些微小错误的叠加就可能会导致非常大的错误。

为什么这个类似监督学习的方法却没有起效果呢？原因很简单，监督学习的数据基于独立同分布，也就是说训练点之间并不会相互影响，但是在模仿学习中，这是一个序列决策的问题，训练点之间是会相互影响的。

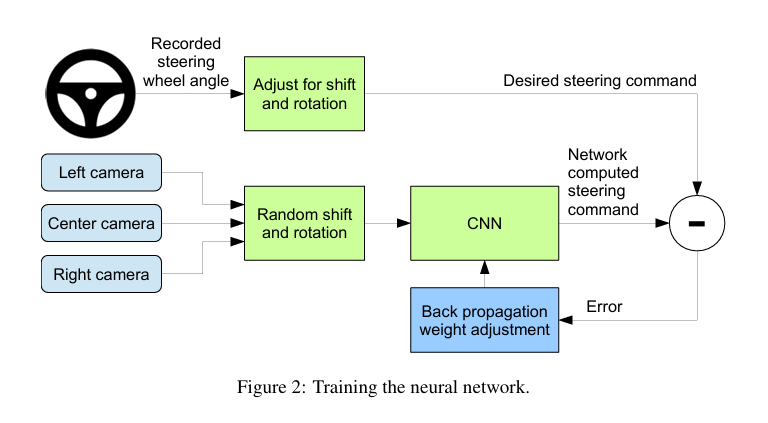
一种方法是引入简单的反馈机制，比如说采用三个摄像头，前、左、右；左边的摄像头会根据路况进行向右修正，右边的摄像头也会根据路况向左修正。

End to End Learning for Self-Driving Cars

---

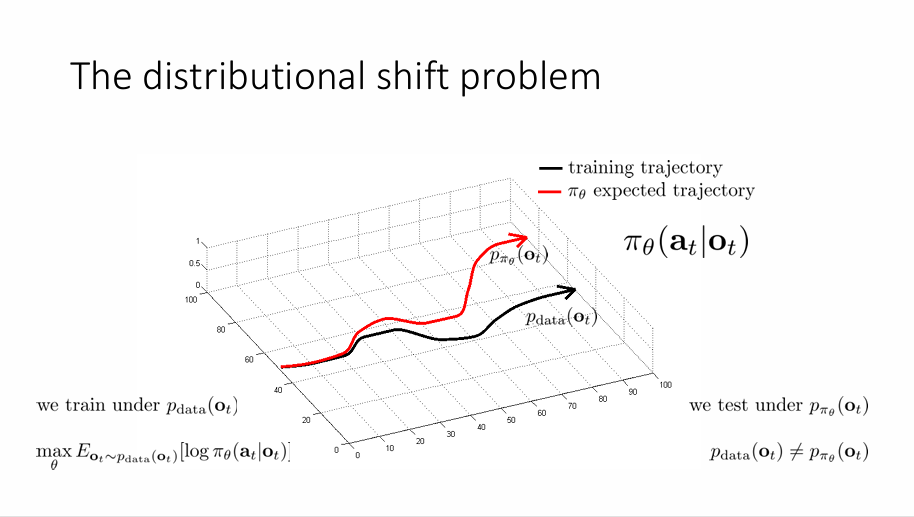
我们用 \(p_{\text{data}}(o_{t})\) 表示产生数据集的分布，用 \(p_{\pi_{\theta}}(o_{t})\) 表示策略。

我们在数据集上训练我们的策略，我们希望产生的策略满足

\[ \max \mathbb{E}_{o_{t}\sim p_{\text{data}}(o_{t})}[\log \pi_{\theta}(a_{t}|o_{t})] \]

我们在 \(p_{\pi_{\theta}}(o_{t})\) 下测试我们的策略，因为 \(p_{\text{data}}(o_{t})\neq p_{\pi_{\theta}}(o_{t})\) 所以策略输出的动作会有所不同，这种行为称为分布偏移

我们定义成本(cost)函数来衡量性能优劣

\[ c(s_{t},a_{t}) = \left\{\begin{aligned} 0&\text{ if }a_{t}= \pi ^{*}(s_{t})\\ 1&\text{ otherwise} \end{aligned}\right. \]

所以我们的目标就是最小化预期成本

\[ \text{minmize } \mathbb{E}_{s_{t}\sim p_{\pi_{\theta}}(s_{t})}[c(s_{t},a_{t})] \]

假定

\[ \pi_{\theta}(a\neq \pi ^{*}(s)|s)\leq \varepsilon \quad \forall s \in \mathcal{D}_{train} \]

\(\varepsilon\) 是一个小量，也就是说在训练状态下，犯错误的概率很小。

假定对于见过的任何状态，犯错误的概率是 \(\varepsilon\) ，但对于没有见过的状态，犯错误的概率是无界。想象一下你是一个走钢丝者，在每个状态下都有完美的动作，即保持在钢丝上，但如果你采取了不正确的动作，如果你犯了错误，你会从钢丝上掉下来。从钢丝上掉下来并不是一件很糟糕的事情（如果做好安全措施的话），真正糟糕的事情是你处在一个未知的状态，给你演示的人并没有告诉掉下来后会做什么。

\[ \mathbb{E}\left[ \sum_{t}^{} c(s_{t},a_{t}) \right]\leq \underbrace{\varepsilon T + (1-\varepsilon)(\varepsilon(T-1)+\dots) }_{T \text{ terms,each }O(\varepsilon T) } \]

假如我们第一步就犯错，犯错误的概率为 \(\varepsilon\) ，这个错误会影响到后续的 \(T\) 个时间步，因此成本会累加到 \(T\)。由于 \(\varepsilon\) 是一个小量，因此 \(1-\varepsilon\) 可以近似取 \(1\) ，那么，所有这些项的数量级大约是 \(\varepsilon T\)，一共有 \(T\) 项，则犯错的成本为 \(\varepsilon T^{2}\) 数量级 。这是一个非常严重的问题，随着时间步的增长，成本呈二次增长，我们更希望其能够呈线性增长。

当然这是一个最坏的情况，他给出了犯错误的上限。

我们不再假定 state 源于数据集，而是满足一定的数据分布 \(s \sim p_{\text{train}}(s)\) ，所以误差

\[ \mathbb{E}_{p_{\text{train}}(s)} [\pi_{\theta}(a\neq \pi ^{*}(s)|s)]\leq\varepsilon \]

如果 \(p_{\text{train}}(s)\neq p_{\theta}(s)\)，我们假定策略的状态分布为两个项的和：

\[ \begin{align} &p_{\theta}(s_{t})= \underset{ \text{probability we made no mistake} }{ (1-\varepsilon)^{t}p_{\text{train}}(s_{t}) }+\underset{ \text{some other distribution} }{ (1-(1-\varepsilon)^{t})p_{\text{mistake}}(s_{t}) } \\ \implies&\lvert p_{\theta}(s_{t})-p_{\text{train}}(s_{t}) \rvert = (1-(1-\varepsilon)^{t})\lvert p_{\text{mistake}}(s_{t})-p_{\text{train}}(s_{t}) \rvert \leq 2(1-(1-\varepsilon)^{t}) \end{align} \]

因为概率小于 \(1\) ，而两个分布之间的差异最坏的情况是 \(2\) （？）

由于 \(\varepsilon\) 是一个小量，运用不等式：\((1-\varepsilon)^{t}\geq 1 - \varepsilon t\) ，因此上述不等式又可以化作

\[ \lvert p_{\theta}(s_{t})-p_{\text{train}}(s_{t}) \rvert\leq 2\varepsilon t \]

将期望展开：

\[ \begin{align} \sum_{t}^{} \mathbb{E}_{p_{\theta}(s_{t})}[c_{t}] == \sum_{t}^{} \sum_{s_{t}}^{}p_{\theta}(s_{t})c_{t}(s_{t}) &\leq \sum_{t}^{} \sum_{_{s_{t}}}^{}p_{\text{train}}(s_{t})c_{t}(s_{t}) + \lvert p_{\theta}(s_{t})-p_{\text{train}}(s_{t}) \rvert c_{\max} \\ & \leq\sum_{t}^{}\varepsilon + 2\varepsilon t \leq \varepsilon T+2\varepsilon T^{2} \end{align} \]

这仍然是一个 \(\mathcal{O}(\varepsilon T^{2})\) 的情况，在最坏的情况下我们得到了 \(\mathcal{O}(\varepsilon T^{2})\) （走钢丝），在这个情况下我们仍得到了 \(\mathcal{O}(\varepsilon T^{2})\)，因此 \(\mathcal{O}(\varepsilon T^{2})\) 实际上是一个界，你没有办法做的比他更糟，这就是行为克隆的结果