Exploration II

约 2654 个字 1 张图片 预计阅读时间 18 分钟

silde

笔记参考

考虑一个完全没有奖励的情境，那么这种情境下我们是否能够恢复多样化的行为呢？从 AI 或者科学的角度的思考这个问题，考虑一个儿童在环境中花了大量时间玩耍，这些行为并没有任何缉拿管理，但是它们并非是随机的，而是出于某种目的，一个简单的驱动力是出自内心的好奇心，从而驱使他们去尝试更多新奇的东西。

那么究竟为什么要在没有奖励的情况下进行探索呢？实际上这使我们能

• 在无监督的情况下学习技能, 再利用这些技能实现其他目标
• 学习一系列子技能并在一些层次的强化学习方案中使用
• 探索所有可能的行为

因此将探索奖励的问题转换成一个获取可以被重新利用的技能的问题。我们期望的是，智能体能够经历一段长时间的无监督学习，然后我们提出一个目标使其能够利用自己习得的技能实现这个目标。

mutual information

对于两个分布 \(p(x)\) 和 \(p(y)\) ，互信息定义为

\[ \mathcal{I}(x;y) = D_{KL}(p(x,y)||p(x)p(y)) = \sum_{x,y} p(x,y) \log \frac{ p(x,y)}{p(x)p(y)} \]

记 \(\pi(\mathbf{s})\) 为策略 \(\pi\) 下状态的边缘分布，\(\mathcal{H}(\pi(\mathbf{s}))\) 表示为对应的熵，考虑互信息

\[ \mathcal{I}(\mathbf{s}_{t+1};\mathbf{a}_{t}) = \mathcal{H}(\mathbf{s}_{t+1}) - \mathcal{H}(\mathbf{s}_{t+1}|\mathbf{a}_{t}) \]

这样一项被称为 "empowerment"，表示当前动作 \(\mathbf{a}_{t}\) 对下一步状态 \(\mathbf{s}_{t+1}\) 的影响力，这是用来度量 agent 在当前状态下对未来的掌控能力，直观上理解就是如果动作几乎决定了未来状态（第二项比较小），也就意味 agent 对未来有很强的掌控力。

Learn without any rewards at all

在 agent 完成了学习之后，如何向 agent 提出自己期望达到的目标呢？从现实角度来说，我们会提供其一个希望它能够达到情境的图片，换言之，我们给他提供完成目标时的状态。 但是状态可能会使比较复杂的（比如说图像），这就需要利用之前所讲的相似性概念。

以变分自编码器这个特定的生成模型为例，我们假定这个生成模型具有图像的某种潜在变量表示，以 \(x\) 表示图像，以 \(z\) 表示在生成模型中图像的潜在表示向量，我们期望对于相似的图像，这些向量之间应该是紧密的。

现在我们关心智能体在无监督阶段的行为，我们期望它能够想象自己的目标并试图达到这些目标。记给定潜在变量对应的图像分布为 \(p_{\theta}(x|z)\) ，潜在变量的分布为 \(p(z)\) ，图像对应的潜在分布 \(q_{\phi}(x|z)\) 。所以训练过程简述为：

1. 提出训练目标： \(z_{g}\sim p(z),x_{g}\sim p_{\theta}(x_{g}|z_{g})\)
2. 尝试利用策略 \(\pi(a|x,x_{g})\) 实现目标 \(\bar{x}\) ，理想情况下是 \(\bar{x}\) 等于 \(x_{g}\)
3. 使用数据更新 \(\pi\)
4. 使用数据更新模型： \(p_{\theta}(x_{g}|z_{g}),q_{\phi}(z_{g}|x_{g})\)

但是生成模型是基于已有数据训练的，因此其生成的数据类似于已经见过的数据。直觉上，我们希望提高很少被访问到的状态的权重，当拟合生成模型时，他会给分布的尾部分配更多的概率，从而扩展可能访问的状态范围。我们对第四步做一些修改，假定我们使用标准的最大似然估计，那么需要改成加权的最大似然估计：

\[ \theta,\phi \leftarrow \arg \max_{\theta,\phi} \mathbb{E}[w(\bar{x})\log p(\bar{x})] \]

所以什么工具可以告诉我们某样东西被见过的频率有多低呢？生成模型在生成数据时，同时也要能生成类似的密度函数 \(p_{\theta}(\bar{x})\) ，因此取 \(w(\bar{x})= p_{\theta}(\bar{x})^{\alpha}\) ，当 \(\alpha \in[-1,0)\) 时，熵增加，这个密度函数使我们的目标提议更多样化

在整个过程中，我们的目标是：

\[ \max \mathcal{H}(p(G)) - \mathcal{H}(p(G|S)) \]

在这个过程中，强化学习利用策略 \(\pi(a|S,G)\) 使我们的状态 \(S\) 更接近于目标状态 \(G\) ，也就意味着 \(p(G|S)\) 更加确定。

实际上，目标也可以写作是状态 \(S\) 和目标状态 \(G\) 之间的互信息：

\[ \max \mathcal{H}(p(G)) - \mathcal{H}(p(G|S)) = \max \mathcal{I}(S;G) \]

这会导致两件事：

• 更多的探索从而增大 \(\mathcal{H}(p(G))\)
• 更有效的实现目标从而降低 \(\mathcal{H}(p(G|S))\)

Exploration with intrinsic motivation

之前在探索中的方法都是让策略尽可能探索新奇的状态。直觉上来说，如果一个状态经常被访问，这就不是一个新奇的状态。此时我们可以设计一个新的奖励函数：

\[ \tilde{r}(\mathbf{s}) = r(\mathbf{s}) - \log p_{\pi}(\mathbf{s}) \]

\(p_{\pi}(\mathbf{s})\) 表示给定策略 \(\pi(\mathbf{a}|\mathbf{s})\) 对应的状态密度。训练过程可以写为：

1. 更新 \(\pi(\mathbf{a}|\mathbf{s})\) 以最大化 \(\mathbb{E}_{\pi}[\tilde{r}(\mathbf{s})]\)
2. 更新 \(p_{\pi}(\mathbf{s})\) 来拟合边缘状态

但是这个做法有一些问题，尽管它能给所有状态分配合理的高概率，但是最终的得到的策略会比较随意，因为它只会去访问次数比较少的地方。我们希望得到的是一个能够随机访问许多不同的地方并从中选择的策略。

回到状态边缘匹配问题，当我们参照上面的方法考虑奖励：

\[ \tilde{r}(\mathbf{s}) =\log p^{*}(\mathbf{s})- \log p_{\pi}(\mathbf{s}) \]

同样也会遇到类似的问题：agent 倾向于去 \(p_{\pi}(\mathbf{s})\) 很小的地方或 \(p^{*}(\mathbf{s})\) 很大的地方探索，这种方法实际上并不能实现状态边缘匹配。原因在于，内在奖励只告诉智能体哪个状态值得去，但没有考虑状态转移的成本。智能体可能会找到一条捷径，迅速到达一个奖励丰厚的区域，然后一直停留在那里，而不会去探索其他需要经过“低奖励”区域才能到达的地方。这导致最终的边缘分布 \(p_{\pi}(\mathbf{s})\) 仍然是局部的，无法匹配整个目标分布 \(p^{*}(\mathbf{s})\)

一个相对简单的方法：

1. 学习 \(\pi^{k}(\mathbf{a}|\mathbf{s})\) 最大化 \(\mathbb{E}[\tilde{r}^{k}(\mathbf{s})]\) ，这里 \(k\) 表示迭代次数
2. 更新 \(p_{\pi^{k}}(\mathbf{s})\) 来拟合过去所有的边缘状态
3. 最终返回 \(\pi ^{*}(\mathbf{a}|\mathbf{s}) = \sum_{k}\pi^{k}(\mathbf{a}|\mathbf{s})\)

从博弈论角度来说，此时我们达到了一种纳什均衡：

• 策略 \(\pi^{k}\) 最大化了当前的奖励
• 边缘分布 \(p_{\pi^{k}}(\mathbf{s})\) 拟合了策略所访问的状态

一种特殊情况是当目标分布是一个均匀分布 \(p^{*}(\mathbf{s}) = C\) 时，最小化 KL 散度就等于最大化边缘分布的熵 \(\symcal{H}(p_{\pi}(\mathbf{s}))\) ，这被称为最大熵探索，在这种情况下，智能体的目标是探索所有状态，并使它们的访问频率尽可能均匀。

现在考虑一个问题，上面所考虑的最大熵的探索是我们能做到的最好的事情嘛？

考虑以下情境：我们先在一个没有奖励的环境中进行充分的探索，在测试时，对手会选择最坏的终点 \(G\) 使我们的策略失效 ，为了防止对手选择一个我们无法到达的状态，我们就需要确保我们的策略能够到达所有可能的有效状态，从数学上来说也就是应当训练使得

\[ p(G) = \arg \max_{p} \mathcal{H}(p(G)) \]

换言之由于我们不知道任何关于 goal 的信息，最大化 entropy 是我们能做的的最好的事情.

Beyond state covering: covering the space of skills

给定状态 \(\mathbf{s}\) 和任务索引 \(z\) ，\(z\) 可以是一个离散或者是连续的变量，其代表了一种特定的行为模式或技能，则我们对应的策略 \(\pi\) 可以写做 \(\pi(\mathbf{a}|\mathbf{s},z)\) ，换言之，它告诉了 agent 在给定状态 \(\mathbf{s}\) 和技能 \(z\) 时应带采取什么行动。

但是达到多样化的目标并不等同于执行多样化的任务，因为并非所有行为都可以被认为时达成目标的行为。举一个例子：一个机器人绕过了一个红色的小球到达了一个绿色区域，我们的目标是到达绿色区域，但是在这个过程中机器人学会了两个技能：绕过小球和到达区域。因此所有可能的技能空间比到达目标的技能空间更大

直觉上来说，不同的技能应该访问不同的状态空间区域，不仅仅是单个不同的状态。

将策略定义成如下形式：

\[ \pi(\mathbf{a}|\mathbf{s},z) = \arg \max_{\pi}\sum_{z}\mathbb{E}_{\mathbf{s}\sim \pi(\mathbf{s}|z)}[r(\mathbf{s},z)] \]

当给定 \(z\) 时，我门希望该技能生成的状态与那些 \(z' \neq z\) 的状态有所区别，从而确保对于每一个 \(z\) ，都能做出独特的行为，一个实现方法时让奖励变成一个分类器：

\[ r(\mathbf{s},z) = \log p(z|\mathbf{s}) \]

训练过程总结为：

1. Agent 选择一个技能 \(z\)。
2. 根据策略与环境交互 → 产生状态。
3. 判别器 D 根据状态 \(\bf s\) 预测技能 \(z\)。
4. 如果预测正确 → 给高奖励；否则 → 奖励低。
5. Agent 于是学习到：每个技能要能产生区分度高的状态。

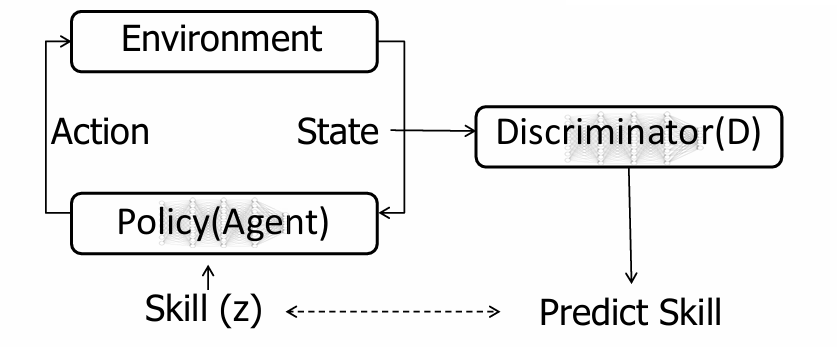
事实上将 \(z\) 和 \(\mathbf{s}\) 的互信息展开能够发现：

\[ \mathcal{I}(z,\mathbf{s}) = \mathcal{H}(z) -\mathcal{H}(z|\mathbf{s}) \]

为了最大化互信息，我们要做两件事：

• 最大化 \(\mathcal{H}(z)\) ，这要求 \(p(z)\) 时均匀分布
• 最小化 \(\mathcal{H}(z|\mathbf{s})\) ，实际上就是最大化 \(\log p(z|\mathbf{s})\) ，也就意味着技能能够很好地被区分。