跳转至

Model-Based Policy Learning

约 4527 个字 4 张图片 预计阅读时间 30 分钟

slides

CS285 深度强化学习 (10): Model-Based Policy Learning - 知乎

我们所讨论的大多数规划方法都是开环方法，意味着它们会针对给定一系列动作的预期奖励进行优化，但开环控制都是次优的。尽管 MPC 方法在每个时间步骤都会重新规划，但每个时间步上规划的结果仍是开环控制，并没有解决这个问题。尽管这使得算法变得相对简单，但其也是算法一个最大的缺点。

在闭环控制中，我们并不是承诺一系列行动，而是承诺一个策略。Agent 观察一个状态，然后产生一个随后遵循的策略，这个策略将为每个可能的状态提供正确答案。

一般而言，策略 \(\pi\) 有两种形式：

  • Global policy：例如神经网络之类的高级函数逼近器，这种方法经常用在 model-free 的情况，这种策略能够在任意时刻给出一个相当不错的动作。
  • Local policy：这些方法在局部范围内表现良好，比如说迭代线性二次调节器，不仅产生线性动作，还会给出反馈控制器。这是一个局部的闭环控制，而非全局的。

我们关注可以用来训练全局策略的方法，同时利用学习得到的模型，获得完整的基于策略和基于模型的强化学习方法。

考虑将反向传播引入到强化学习中，构建如下计算图 ，使我们能够计算给定策略的奖励总和：

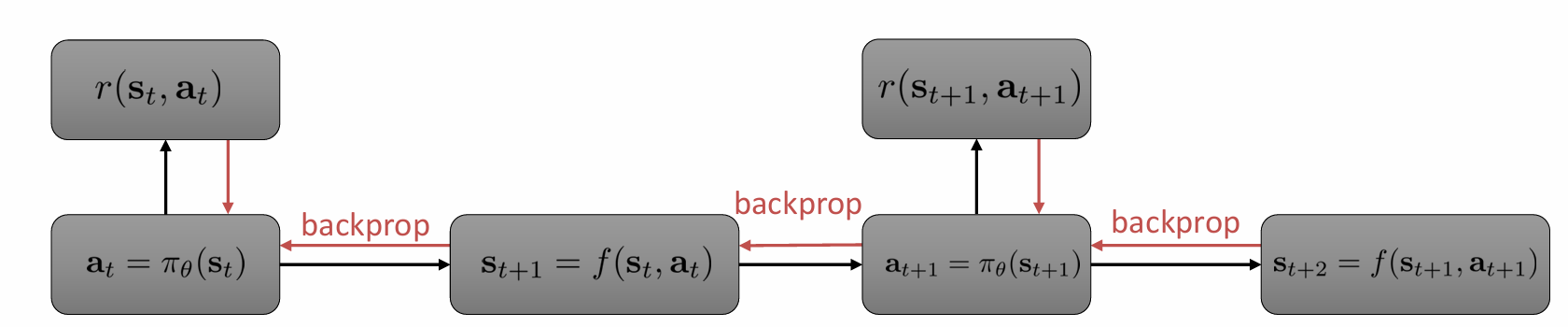
alt text

在这个计算图中有三种类型函数：策略函数，他们接收状态并产生动作；动态函数，接受状态和动作，并产生下一个状态；奖励函数，接受状态和动作并产生一个标量值。这种计算图适用于一些确定性的系统和特定类型的随机系统。

现在的问题，这种方法能够优化我们的 \(\pi_{\theta}\) 嘛？答案是不行。首先，这种思想对应如下算法：

model-based reinforcement learning version 2.0

  1. 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\)，收集 \(\mathcal{D} = \left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)
  2. 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert^{2}\)
  3. 通过反向传播来 optimize policy \(\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})\).
  4. 添加 \((\mathbf{s},\mathbf{a},\mathbf{s}')\) 到 \(\mathcal{D}\), 重复 2−4.

轨迹中早期的动作的未来的影响会逐渐累积，而末端动作的影响相对较小，因此，你对轨迹开始时的动作有很大的梯度，从而对策略参数有很大的梯度，与之相对的末端的梯度就比较小，这会导致一个病态情况。这个问题的性质类似于我们在射击法和轨迹优化中遇到的参数敏感性问题，在之前的方法中，我们利用二阶信息解决了这个问题；但在这个问题中，策略参数耦合了所有的时间步，所以没有办法从末端开始并逐步向后的方法来解决这个问题，同时二阶优化器在神经网络也常常是不稳定的。

从另一个角度说，这个问题和利用反向传播训练 RNN 网络的情形类似：前向时间长导致梯度爆炸，后向时间长导致梯度消失。在 RNN 中，我们可以自行选择动态特性，但是在这个问题中我们并不能自行选择，因此也没法使用 LSTM 方法。我们很难使用深度学习中的大多数方法，因为这些方法从根本上改变函数，使其成为一个更易于求导的函数。

一个解决方法是利用 derivative-free RL 算法，这些算法将生成样本，这看起来有点反常，因为如果我们学习一个模型，我们并没有利用模型已知或具有已知导数这一事实，而是假装其为环境的模拟器，并用其模拟更多数据。这是我们能够做到效果最好的方法。

Model-Free Learning With a Model

反向传播梯度表达式：

\[ \nabla_{\theta}J(\theta) = \sum_{ t=1}^{T} \frac{{\rm{d}} \mathbf{a}_{t} }{{\rm {d}} \theta } \frac{{\rm{d}} \mathbf{s}_{t+1} }{{\rm {d}} \mathbf{a}_{t} } \left( \sum_{t'=t+1}^{T}\frac{{\rm{d}} r_{t'} }{{\rm {d}} \mathbf{s}_{t'} }\left( \prod_{t''=t+2}^{t'} \frac{{\rm{d}} \mathbf{s}_{t''} }{{\rm {d}} \mathbf{a}_{t''-1} }\frac{{\rm{d}} \mathbf{a}_{t''-1} }{{\rm {d}}\mathbf{s}_{t''-1} }+\frac{{\rm{d}} \mathbf{s}_{t''} }{{\rm {d}}\mathbf{s}_{t''-1} } \right) \right) \]

这个式子看起来很复杂，但实际上只是利用链式法则将其一步步展开。可以看到第二个括号内一系列连乘的 Jacobian 矩阵，如果这些矩阵在某些方向上的最大特征值大于 \(1\) ，那么沿那个方向的分量会指数级放大，导致梯度爆炸；与之相对的，如果在某些方向上的最大特征值小于 \(1\) ，那么沿这些方向的分量就会指数级衰减，这就是梯度难以处理的原因。

回到 Policy gradient 算法：

\[ \nabla_{\theta}J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})\hat{Q}_{i,t}^{\pi} \]

可以看出，此时我们摆脱了 Jacobian 矩阵的影响，但计算策略梯度本身需要采样，这是为了摆脱 Jacobian 矩阵所需要付出的代价。因此，如果采到的样本足够多，策略梯度方法会比反向传播算法更稳定。在 Model-free 算法中，收集样本是一个比较困难的事情，但是此时我们已经有了一个模型，因此我们只需要做的就是执行模型收集样本。

model-based reinforcement learning version

  1. 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\)， 收集 \(\mathcal{D}=\left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)，
  2. 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert^{2}\)
  3. 利用 \(f\) 与 policy \(\pi_{\theta}(\mathbf{a}|\mathbf{s})\) 生成 \(\left\{ \tau_{i} \right\}\) 
  4. 利用 \(\left\{ \tau_{i} \right\}\) 改进 \(\pi_{\theta}(\mathbf{a}|\mathbf{s})\) ， 重复 3- 4.
  5. 运行 \(\pi_{\theta}(\mathbf{a}|\mathbf{s})\) 来收集数据, 添加到 \(\mathcal{D}\) ，重复 2- 5.

这个算法的问题和在 Model-free 中讨论的一样：我们的误差会随着时间逐渐增大，从而导致分布偏移，同时算法将采用偏移的模型生成样本用于训练，这实际上会增大偏移的严重程度，就像在行为克隆中讨论的，它将以 \(\mathcal{O}(\varepsilon T^{2})\) 的速度累计错误。

要减少长时间的推演，因为其会导致较大的误差累计 ，一个做法是使用比较小的时间推演，尽管这能够降低误差积累，但实际上改变问题，而且模型无法预测较长时间的行为。另一个做法是随机抽取现实的状态，然后再这些状态上作小规模推演，将其与少量长时间推演结合。但问题是，这对应一个非常复杂的策略，也就是说当我们执行策略到某个抽取的状态时，模型会切换他的策略，这会导致一个混合的状态分布。

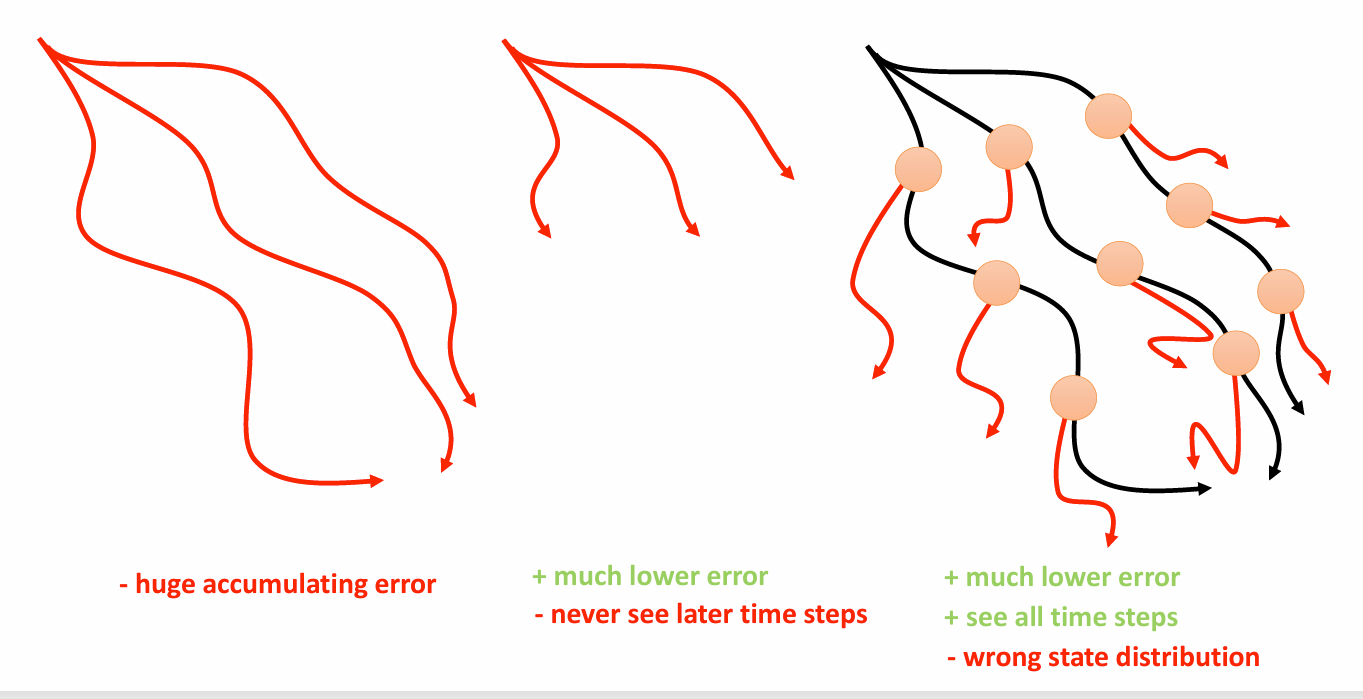
alt text

model-based reinforcement learning version 3.0

  1. 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\)， 收集 \(\mathcal{D}=\left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)，
  2. 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert^{2}\)
  3. 选择 \(\mathcal{D}\) 中的状态 \(\mathbf{s}_{i}\) ，利用 \(f\) 生成短的 rollouts
  4. 利用real data 与 model data 改进 \(\pi_{\theta}(\mathbf{a}|\mathbf{s})\) ， 重复 3- 4.
  5. 运行 \(\pi_{\theta}(\mathbf{a}|\mathbf{s})\) 来收集数据, 添加到 \(\mathcal{D}\) ，重复 2- 5.

Dyna-Style Algorithms

Dyna 是上述算法的一个特定版本。它所使用的基于模型的回溯长度恰好为一个时间步长。Dyna 采用 online Q learning ，通过一个模型执行无模型学习。

Dyna

  1. 给定状态 \(\mathbf{s}\) ，使用 exploration policy 选择 action \(\mathbf{a}\)
  2. 观测 \(\mathbf{s}',r\) ，得到转移 \((\mathbf{s},\mathbf{a},\mathbf{s}',r)\)
  3. 利用 \((s,a,s')\) 更新 dynamic model 和 reward model
  4. \(Q\) 更新：\(Q(\mathbf{s},\mathbf{a})\leftarrow Q(\mathbf{s},\mathbf{a})+\alpha \mathbb{E}_{\mathbf{s}',r}[r+\max_{\mathbf{a}'}Q(\mathbf{s}',\mathbf{a}')-Q(\mathbf{s},\mathbf{a})]\)
  5. 重复以下步骤 \(K\) 次
    1. 采样 \((\mathbf{s},\mathbf{a})\sim \mathcal{B}\)
    2. \(Q\) 更新 \(Q(\mathbf{s},\mathbf{a})\leftarrow Q(\mathbf{s},\mathbf{a})+\alpha \mathbb{E}_{\mathbf{s}',r}[r+\max_{\mathbf{a}'}Q(\mathbf{s}',\mathbf{a}')-Q(\mathbf{s},\mathbf{a})]\) ，这里的 \(\mathbf{s}',r\) 都是从 model 中采样得到的。

Dyna 中做出的选择一定程度上是为了高度随机系统。Dyna 做出的选择可能并不是模型对应最大性能的决策，但这些决策在预期模型对分布偏移非常敏感的时候是好的。

现在更经常使用的是如下广义 Dyna 版本：

  1. 收集数据和转移 \((\mathbf{s},\mathbf{a},\mathbf{s}',r)\)
  2. 学习模型 \(p(\mathbf{s}'|\mathbf{s},\mathbf{a})\)
  3. 重复以下步骤 \(K\) 次：
    1. 从 buffer 中采样 \(\mathbf{s}\sim \mathcal{B}\)
    2. 选择动作 \(\mathbf{a}\)
    3. 模拟 \(\mathbf{s}'\sim \hat{p}(\mathbf{s}'|\mathbf{s},\mathbf{a})\)
    4. 用 model-free RL 算法训练 \((\mathbf{s},\mathbf{a},\mathbf{s}',r)\)
    5. （可选） 进行 \(N\) 步 model-based steps

Model-acclerated 算法的示意图如下所示，这个示意图有助于对算法系统上的理解

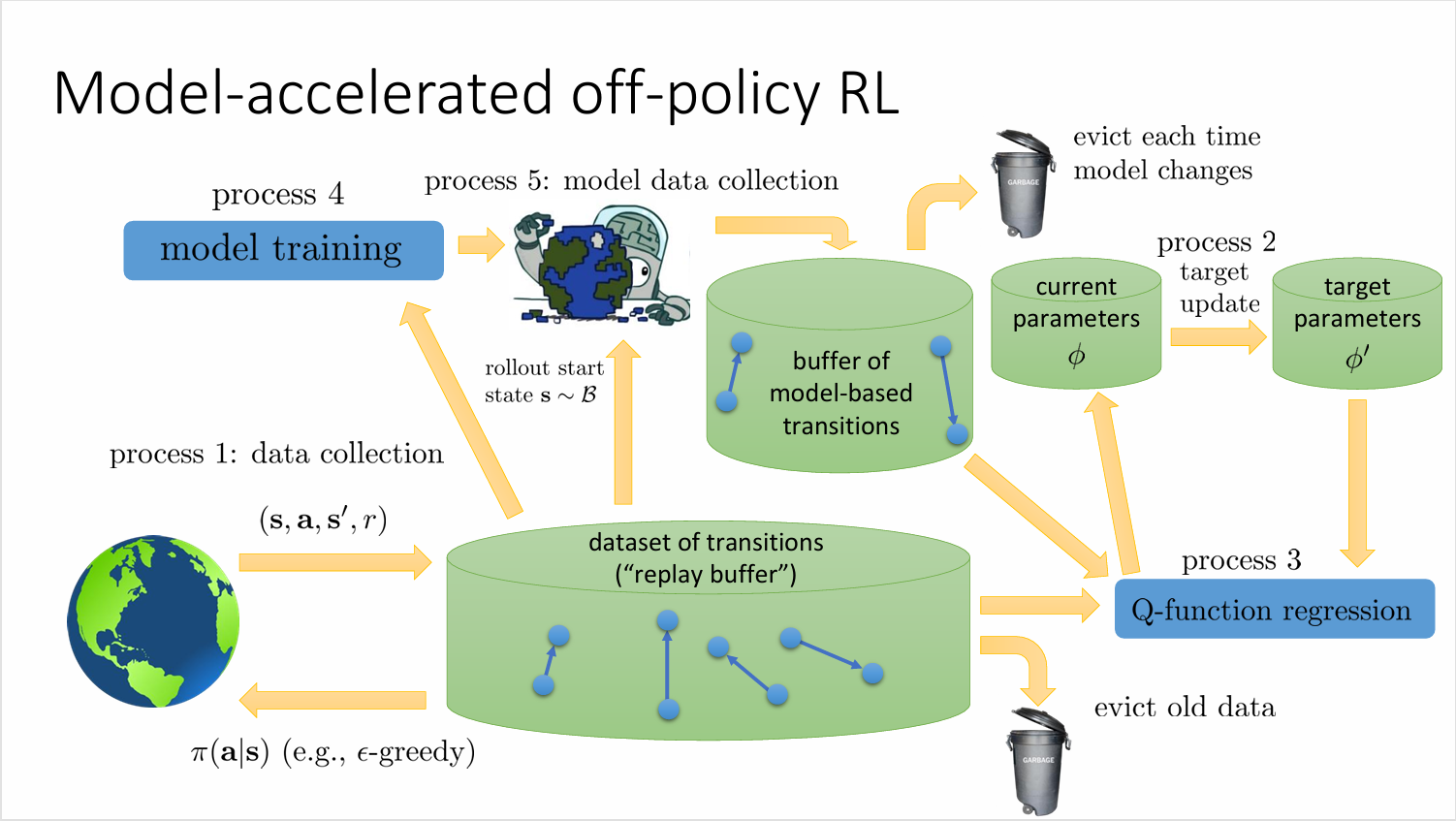
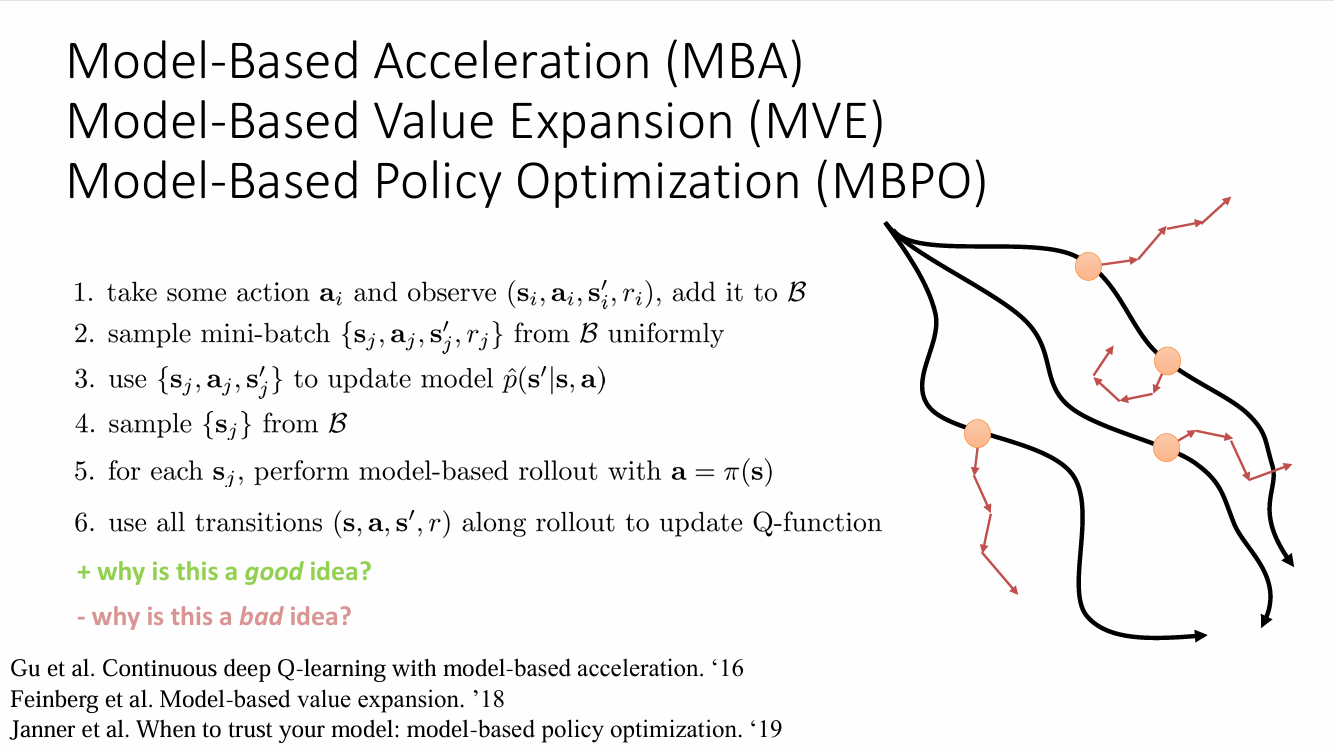
alt text

诸如 Model-Based Acceleration (MBA)，Model-Based Value Expansion (MVE)，Model-Based Policy Optimization (MBPO) 等变体算法都是遵循一定的过程，这些算法仅是在设计决策上略有不同，尤其是在 Q 学习中用到的数据以及使用方法。好处就是这些算法都充分利用了样本数据，但坏处就是这些方法引入更多的误差，同时，短回溯给出的状态介于收集数据的策略的状态分布和最新策略状态分布之间，是二者的混合，这可能会使得算法远离所需的状态，这需要我们利用更多现实数据刷新缓冲区。

alt text

Multi-Step Models & Successor Representation

目前接触到的 RL 方法通常分为两类：

  • Model-free : 直接学习每个状态的价值 \(V(s)\) 或状态-动作对的价值 \(Q(s,a)\)，而不去理解环境的动态。这很高效，但如果奖励函数发生变化，就需要从头重新学习所有价值。
  • Model-based : 显式地学习环境的转移矩阵（从一个状态到另一个状态的概率）和奖励函数。这非常灵活，当奖励函数或环境动态变化时，可以快速更新价值函数，但计算成本高昂。

考虑需要怎么样的模型来评估策略。对于传统情况，我们拟合模型 \(f(\mathbf{s},\mathbf{a})\) 以模拟策略并估计回报。

采用下面这种模型来估计策略

\[ J(\pi) = \mathbb{E}_{s \sim p(s_{1})}[V^{\pi}(s_{1})] \]

为了方便研究，考虑仅依赖状态的价值函数：

\[ \begin{align} V^{\pi}(s_{t} ) &= \sum_{t=t'}^{\infty}\mathbb{E}_{p(s_{t'}|s_{t})}[r(\mathbf{s}_{t'})] \\ &=\sum_{t= t'}^{\infty} \gamma^{t-t'}\sum_{\mathbf{s}}p(\mathbf{s}_{t'}=\mathbf{s}|\mathbf{s}_{t})r(\mathbf{s}) \\ &= \sum_{\mathbf{s}} \left( \sum_{t'=t}^{\infty} \gamma^{t'-t}p(\mathbf{s}_{t'}=\mathbf{s} |\mathbf{s}_{t}) \right) r(\mathbf{s}) \end{align} \]

定义

\[ p_{\pi} (\mathbf{s}_{\mathrm{future} }=\mathbf{s}|\mathbf{s}_{t} ) = (1-\gamma)\sum_{t'=t}^{\infty}\gamma^{t'-t}p(\mathbf{s}_{t'}=\mathbf{s}|\mathbf{s}_{t}) \]

参数 \((1-\gamma)\) 是为了满足归一化条件。这个式子有两种理解方式：

  • 从参数为 \(\gamma\) 的几何分布中随机抽取一个时间步并对评估 \(p(\mathbf{s}_{t'}=\mathbf{s}|\mathbf{s}_{t})\)
  • 在每一个时间步，有 \(1-\gamma\) 的概率停止，则恰好对应状态 \(\mathbf{s}\) 的概率。

应用我们新引入的概念，可以得到：

\[ V^{\pi}(\mathbf{s}_{t}) = \frac{1}{1-\gamma} \sum_{\mathbf{s}}p_{\pi}(\mathbf{s}_{\mathrm{future}}=\mathbf{s}|\mathbf{s}_{t}) r(\mathbf{s}) \triangleq \mu^{\pi}(\mathbf{s}_{t})r(\mathbf{s}) \]

其中

\[ \mu^{\pi}_{i}(\mathbf{s}_{t}) = p_{\pi}(\mathbf{s}_{\mathrm{future}}=i{|\mathbf{s}}_{t}) \]

这个向量表示称作继承表示(Successor Representation)，其提供了一种在 model-free 和 model-base 学习之间取得平衡的方法。 \(\mu_{i}\) 表示从状态 \(\mathbf{s}_{t}\) 出发，在遵循策略 \(\pi\) 的情况下，未来访问状态 \(i\) 的概率。这个向量与奖励无关，但并不独立于模型，取决于策略 \(\pi\) 和环境的转移结构，更多的是价值函数与模型的混合体。

将继承表示转换成 Bellman 形式：

\[ \begin{align} &(1-\gamma)\sum_{t'=t}^{\infty}\gamma^{t'-t}p(\mathbf{s}_{t'}=i|\mathbf{s}_{t}) \\ =&(1-\gamma) \delta(\mathbf{s}_{t}=i) +\gamma \sum_{\mathbf{s}}p(\mathbf{s}|\mathbf{s}_{t})\mu_{i}(\mathbf{s}) \\ =& (1-\gamma)\delta(\mathbf{s}_{t}=i) + \gamma \mathbb{E}_{\mathbf{a}_{t}\sim \pi(\mathbf{s}_{t}|\mathbf{a}_{t}),\mathbf{s}_{t+1}\sim p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})}[\mu^{\pi}_{i}(\mathbf{s}_{t+1})] \end{align} \]

第一项可以视作是一个即时回报项，即在当前状态获得的“奖励”。第二个是一个下一状态的期望项，表示从当前状态出发，在下一步到达所有可能的下一个状态的继承表示之和。也就是说继承表示的更新公式从形式上与 Bellman 方程完全相同，这不过此时的即时奖励是一个特殊函数。

但是继承也面临如下问题：

  • 学习继承表示是否比无模型强化学习更容易
  • 如何扩展到大型状态空间
  • 如何扩展到连续状态空间

现在将继承扩展到大型空间中，在比较大的空间中，继承向量可能非常大，因此与其直接使用继承本身，不如将继承投影到某个基上。考虑奖励展开成如下形式

\[ r(\mathbf{s}) =\sum_{j}^{} \phi_{j}(\mathbf{s}) w_{j} = \phi(\mathbf{s})^{T}\mathbf{w} \]

其中 \(\phi\) 是我们人为设定的映射，\(\mathbf{w}\) 是权重函数，将奖励带入价值函数：

\[ \begin{align} V^{\pi}(\mathbf{s}_{t} ) & = \mu^{\pi}(\mathbf{s}_{t})\vec{r} \\ & = \mu^{\pi}(\mathbf{s}_{t} ) \phi(\mathbf{s})^{T}\mathbf{w} \\ &= \sum_{j} \mu^{\pi}(\mathbf{s}_{t})\vec{\phi}_{j} \mathbf{w} \\ &= \sum_{j}\psi^{\pi}_{j}(\mathbf{s}_{t})^{T} \mathbf{w} \\ & = \psi^{\pi}(\mathbf{s}_{t})^{T} \mathbf{w} \end{align} \]

称 \(\psi^{\pi}\) 为继承特征。也就是说，如果我们能用一些基来表示奖励函数，那么我们就可以构建上述的继承特征表示。如果特征的数量远少于状态的数量，学习他们就会更加方便。

继承特征的 Bellman 形式：

\[ \psi^{\pi}_{j}(\mathbf{s}_{t}) = \phi_{j}(\mathbf{s}_{t}) + \gamma \mathbb{E}_{\mathbf{a}_{t}\sim \pi(\mathbf{s}_{t}|\mathbf{a}_{t}),\mathbf{s}_{t+1}\sim p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})}[\psi^{\pi}_{i}(\mathbf{s}_{t+1})] \]

实际上继承的 Bellman 形式可以视作 \(\phi_{i}(\mathbf{s}_{t})=(1-\gamma)\delta(\mathbf{s}_{t}=i)\) 的特例。同样的，我们也可以构造类似 Q-function 的继承特征，依旧假定 \(r(\mathbf{s}_{t})=\phi(\mathbf{s})^{T}\mathbf{w}\)

\[ Q^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t}) \approx \psi^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t})^{T}\mathbf{w} \]

对于 Bellman 形式：

\[ \psi^{\pi}_{j}(\mathbf{s}_{t},\mathbf{a}_{t}) = \phi_{j}(\mathbf{s}_{t}) + \gamma \mathbb{E}_{\mathbf{a}_{t}\sim \pi(\mathbf{s}_{t}|\mathbf{a}_{t}),\mathbf{s}_{t+1}\sim p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})}[\psi^{\pi}_{i}(\mathbf{s}_{t+1},\mathbf{a}_{t+1})] \]

那么我们如何使用后继特征呢？一个想法是快速回复 \(Q\) 函数。

recover a Q-function very quickly

  1. 训练 \(\psi^{\pi}_{j}(\mathbf{s}_{t},\mathbf{a}_{t})\)
  2. 获取 \(\left\{ \mathbf{s}_{i},r_{i} \right\}\)
  3. \(\mathbf{w}\leftarrow \arg \min_{w} \lVert \phi(\mathbf{s}_{i})^{T}\mathbf{w}-r_{i} \rVert^{2}\)
  4. 恢复 \(Q^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t} ) \approx \psi^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t})^{T}\mathbf{w}\)

而我们的策略就是：

\[ \pi'(\mathbf{s}) = \arg \max_{\mathbf{a}}\psi^{\pi}(\mathbf{s},\mathbf{a})^{T}\mathbf{w} \]

但是得到的并不是最优的 \(Q\) 函数，因为这只是策略 \(\pi\) 的 \(Q\) 函数。当我们做一步策略迭代后，得到的策略 \(\pi'\) 优于 \(\pi\) ，但一般不会是最优的。也就是说我们能够快速恢复 \(Q\) 函数，但是不能快速恢复最优的 \(Q\) 函数。

更好的想法是我们恢复更多的 \(Q\) 函数

recover many Q-functions

  1. 训练一系列 \(\psi_{j}^{\pi_{k}}(\mathbf{s}_{t},\mathbf{a}_{t})\)
  2. 获取 \(\left\{ \mathbf{s}_{i},r_{i} \right\}\)
  3. \(\mathbf{w}\leftarrow \arg \min_{w} \lVert \phi(\mathbf{s}_{i})^{T}\mathbf{w}-r_{i} \rVert^{2}\)
  4. 恢复 \(Q^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t} ) \approx \psi^{\pi_{k}}(\mathbf{s}_{t},\mathbf{a}_{t})^{T}\mathbf{w}\)

对应的策略是：

\[ \pi'(\mathbf{s}) = \arg \max_{\mathbf{a}}\max_{k}\psi^{\pi_{k}}(\mathbf{s},\mathbf{a})^{T}\mathbf{w} \]

因此我们在不同的状态下选择不同的最优策略。

现在考虑如何将继承扩展到连续空间中。在连续空间中，与其学习一个继承表示，不如考虑学习如下二类分类器：

\[ p^{\pi}(F = 1 |\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}}) \]

在这里 \(F =1\) 意味着 \(\mathbf{s}_{future}\) 是在给的 \(\mathbf{s}_{t},\mathbf{a}_{t}\) 情况下策略 \(\pi\) 给出的未来状态。

假定正样本满足 \(D_{+}\sim p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})\) ，负样本满足 \(D_{-}\sim p^{\pi}(\mathbf{s})\) ，那么贝叶斯最优分类器为：

\[ p^{\pi}(F = 1 |\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}}) =\frac{p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})}{p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})+p^{\pi}(\mathbf{s}_{\mathrm{future}})} \]
\[ p^{\pi}(F = 0|\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}}) =\frac{p^{\pi}(\mathbf{s}_{\mathrm{future}})}{p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})+p^{\pi}(\mathbf{s}_{\mathrm{future}})} \]

当我们训练如上分类器后就能从中恢复 \(p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})\)

\[ \frac{p^{\pi}(F = 1|\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}}) }{p^{\pi}(F = 0|\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}}) } p^{\pi}(\mathbf{s}_{\mathrm{future}}) = p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t}) \]

The C-Learning algorithm

  1. 获取负样本：采样 \(\mathbf{s}\sim p^{\pi}(\mathbf{s})\)
  2. 获取正样本：采样 \(\mathbf{s}\sim p^{\pi}(\mathbf{s}_{\mathrm{future}}|\mathbf{s}_{t},\mathbf{a}_{t})\)
  3. 训练分类器：更新 \(p^{\pi}(F = 1|\mathbf{s}_{t},\mathbf{a}_{t},\mathbf{s}_{\mathrm{future}})\)