Value Function Methods
约 3590 个字 2 张图片 预计阅读时间 24 分钟
笔记参考:强化学习CS285笔记【五】价值函数计算(Value Function) - 知乎
我们现在有一个想法是,我们是否可以完全省略策略梯度,也就是如果我们只学习一个价值函数,然后尝试用价值函数决定如何动作,那会怎么样呢?这种想法的直觉在于,价值函数告诉我们哪些状态比其他状态更好,因此如果我们简单地选择那些能够进入更好状态的动作,也许我们就不再需要一个显式的神经网络。
优势函数 \(A^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t})\) 衡量了动作 \(\mathbf{a}_{t}\) 与策略 \(\pi\) 给出的平均动作的好坏。如果我们选取 \(\arg \max_{\mathbf{a}_{t}}A^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t})\) ,则描述了在策略 \(\pi\) 情况下基于 \(\mathbf{s}_{t}\) 所选择的最好的动作,这个动作至少会和其他由策略给出的动作一样好,尽管我们不一定知道策略 \(\pi\) 。
因此,与其考虑显式策略,不如考虑如下隐式策略分布:
也就是说,我们不再找显式的策略分布 \(\pi\) 而是找一个隐式的策略分布:找到最大的 advantage 来作为一个策略,这本质上是做一个搜索优化的过程。在训练中,我们只需要训练我们的优势函数(Q函数或V函数)即可
policy iteration algorithm
- 评估 \(A^{\pi}(\mathbf{s},\mathbf{a})\)
- 设定 \(\pi \leftarrow \pi'\)

我们选择评估 \(V^{\pi}(\mathbf{s})\) ,一种评估方法是采用动态规划(Dynamic programming) 。假设我们已经知道转移概率模型, \(p(\mathbf{s'}|\mathbf{s},\mathbf{a})\) ,并且状态 \(\mathbf{s}\) 和动作 \(a\) 都是小且离散的,这种方法可以使我们用表格来存储值函数。
值函数的 Bootstrapped 更新方式为:
因为我们选择的是最优动作,这是一个确定性的策略,此时更新方式修改为:
如果将期望展开:
注意此时转移概率是一个常数,因此可以看出每一个 \(V^{\pi}(\mathbf{s})\) 是一组变量的线性组合,实际上,取:
定义转移概率矩阵:
那么整组更新公式可以写成:
移项得到:
这就是一个线性方程组。
在计算隐式策略 \(\pi'\) 时,我们计算了优势函数的 \(\arg \max\) ,回顾优势函数的定义:
注意到后一项与动作 \(\mathbf{a}\) 无关,前两项是 \(Q\) 函数,因此当我们计算优势函数关于动作的 \(\arg \max\) ,我们其实是在计算 \(\arg \max_{\mathbf{a}_{t}}Q^{\pi}(\mathbf{s}_{t},\mathbf{a}_{t})\) 。在这种情况,我们可以简化我们的迭代过程:
value iteration algorithm
- 取 \(Q(\mathbf{s},\mathbf{a})\leftarrow r(\mathbf{s},\mathbf{a})+\gamma \mathbb{E}[V(\mathbf{s}')]\)
- 取 \(V(\mathbf{s})\leftarrow \max_{\mathbf{a}}Q(\mathbf{s},\mathbf{a})\)
这是因为,我们考虑的动态规划实际上是做一个求解固定点的方程,我们并不关心中间策略,而是只关心最优值函数 \(V^{*}\) 因此在每轮迭代中直接做“完美”的策略提升。
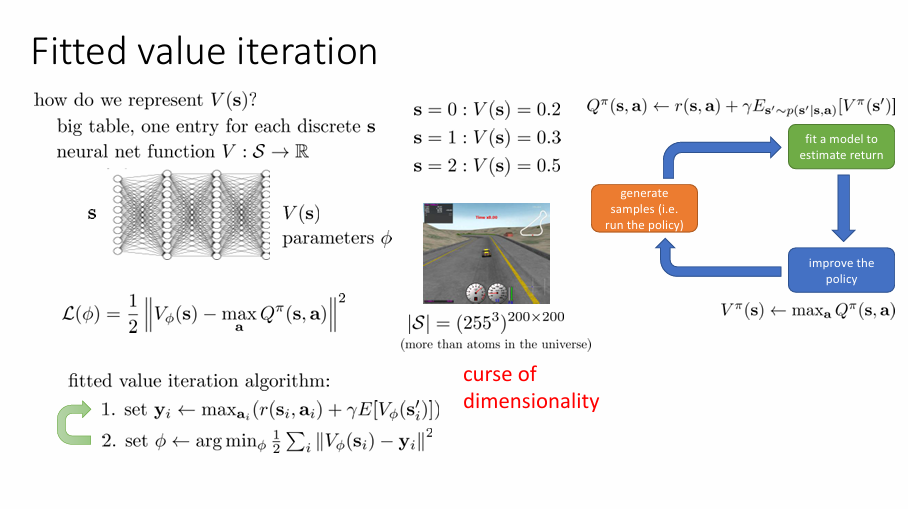
之前的讨论都是建立在比较小且离散的状态空间中,从而可以利用表格枚举每个可能状态 ,现在讨论如何引入利用神经网络和函数逼近器。我们不可能总是用表格来枚举每个可能状态,随着维度的增大,在表格中所需要的格子数会使维度的数量的指数级,这也被称为“维度的诅咒”(curse of dimensionality)。
用神经网络对价值函数做一个拟合,如果我们采用的是值迭代方法,损失函数定义为:
fitted value iteration algorithm
- 设定 \(\mathbf{y}_{i}\leftarrow \max_{\mathbf{a}_{i}}(r(\mathbf{s}_{i},\mathbf{a}_{i})+\gamma \mathbb{E}[V_{\phi}(\mathbf{s}'_{i})])\)
- 设定 \(\phi \leftarrow \arg \min_{\phi} \frac{1}{2}\sum_{i}^{}\lVert V_{\phi}(\mathbf{s}_{i})-\mathbf{y}_{i} \rVert\)
但是,在计算期望 \(\mathbb{E}[B_{\phi}(\mathbf{s}_{i}')]\) 的时候,我们需要利用转移分布 \(p(\mathbf{s}'|\mathbf{s},\mathbf{a})\) 来计算期望,但是我们并不能知道显式的概率分布,也无法准确地回到原来状态,因此需要对算法进行修改。首先,回顾 Policy 迭代过程,我们用价值函数来评估 \(Q^{\pi}(\mathbf{s},\mathbf{a})\) ,因此,不如直接采用 \(Q^{\pi}(\mathbf{s},\mathbf{a})\) 函数来迭代,即
此时,我们只需要知道状态 \(\mathbf{s}'\) 就可以更新目标值,其次,为了避免知道转移概率,引入 \(\max\) 技巧,直接在 \(Q\) 函数中寻找最大值,也就是:
整理上面讨论的,可得
full fitted Q-iteration algorithm
- 收集离散数据 \(\left\{ (\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}_{i}',r_{i}) \right\}\)
- 设定 \(\mathbf{y}_{i}\leftarrow \max_{\mathbf{a}_{i}}(r(\mathbf{s}_{i},\mathbf{a}_{i})+\gamma \max_{\mathbf{a}_i'}Q_{\phi}(\mathbf{s}'_{i},\mathbf{a}_i')\)
- 设定 \(\phi \leftarrow \arg \min_{\phi} \frac{1}{2}\sum_{i}^{}\lVert Q_{\phi}(\mathbf{s}_{i},\mathbf{a}_i)-\mathbf{y}_{i} \rVert\)
Summary
我们用 Q 函数来迭代,是因为它绕过了显式策略表示,可以直接从状态-动作对进行学习与优化,特别适合于最优策略学习和 off-policy 强化学习。
注意此时 FQI 算法是一个离线算法(off-policy)这是因为用于训练的数据集是在开始前就被收集好的,我们的策略是在更新时对 \(Q\) 函数取 \(\arg \max\) , 想象这是一个模型,\(Q\) 函数允许你模拟如果你采取不同的动作会得到什么样的值,因此我们就能知道哪个动作是好的。这就是为什么我们不要样本,我们基本上是利用 \(Q\) 函数来模拟新动作的值。
Example
就像你在一个游戏里练习打怪兽:
- 你不需要每次都真的打一次来看看会不会赢
- 你训练了一个模型 Q,它能告诉你:“如果你用技能 A 打这个怪,可能赢;技能 B 就危险”
- 所以你根本不需要再打一次试试,就能做出最优选择
同时,当我们给定了 \(\mathbf{s}\) 和 \(\mathbf{a}\) 时,转移概率 \(p(\mathbf{s}'|\mathbf{s},\mathbf{a})\) 是独立于策略 \(\pi\),如果我们固定 \(\mathbf{s}\) 和 \(\mathbf{a}\) ,无论我们如何改变 \(\pi\) ,\(\mathbf{s}'\) 都不会改变,因为 \(\pi\) 只会影响输出的 \(\mathbf{a}\) 。
那么在 FQI 算法中,我们究竟在优化什么呢?算法的第二步在改进我们的策略,而算法的第三步给出误差表达式:
实际上,我们真正优化的是如上表达式,我们把这一项称为 Bellman error,但是这个误差本身并不能真正反映策略的好坏,只是描述能够复制目标值的准确度。如果 \(\mathcal{E} =0\) ,这就是我们要最优 \(Q\) 函数,对应最优策略。但是,这个结论适用于表格情况,其他情况不一定适合。
我们可以通过为超参数做出特定选择来实例化算法,这实际上对应一种在线学习:
online Q iteration algorithm
- 采取一些动作 \(\mathbf{a}_{i}\) ,并收集数据 \((\mathbf{s}_{i},\mathbf{a}_{i},\mathbf{s}_{i}',r_{i})\)
- \(\mathbf{y}_{i}\leftarrow r(\mathbf{s}_{i},\mathbf{a}_{i})+\gamma \max_{\mathbf{a}'}Q_{\phi}(\mathbf{s}_{i}',\mathbf{a}_{i}')\)
- \(\phi \leftarrow \phi - \alpha \frac{{\rm{d}} Q_{\phi} }{{\rm {d}} \phi }(\mathbf{s}_{i},\mathbf{a}_{i})(Q_{\phi}(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{y}_{i})\)
这也被称为 Watkins Q 学习,是经典的 Q 学习算法 。
Online Q-iteration 算法和之前的 Q-iteration 算法区别在于,Online Q-iteration 在 step 1 的时候只需要收集一个数据,在step2和3只需要迭代一步就行 不需要反复迭代 \(K\) 次,最后就是在step3 采用的是梯度更新而不是求解优化问题。——摘自参考
在学习中,使用贪婪算法并不是一个好的选择,一个原因是这个算法是确定性,如果我们的初始 \(Q\) 函数非常糟糕,我们的 \(\arg\max\) 算法可能会导致对于任意特定状态都采取相同的动作(相当于陷入了一种局部最优。),如果这个动作并不是一个很好的动作,我们可能很难找到比他好的动作。于是我们应当注入一点随机性来避免这种情况,基于这种想法的一种贪婪算法是 "epsilon-greedy",即:
也就是我们分配了一定概率给非贪心的动作,如果我们选择 epsilon 比较小,那么我们大部分时间都会都会保持选择最好的动作,但是我们还有一点概率选择其他动作,以防我们一直选择的动作不够好。
还有一种方法是引入变化,常见的变化是指数变化:
在这种情况下,那些几乎和最好的动作一样好的动作会被相当频繁地采取。这种方法称为 “Boltzman exploration” 在多数情况下比 epsilon greedy 更受欢迎。
Value Functions in Theory
现在探讨 Value iteration 的收敛性:定义一个 Bellman 算子:
其中 \(r_{\mathbf{a}}\) 表示了当前动作 \(\mathbf{a}\) 对应的奖励函数,\(\mathcal{T}_{\mathbf{a}}\) 表示对于固定动作 \(\mathbf{a}\) ,进行转移的线性算子,比如说马尔可夫转移矩阵: \(\mathcal{T}_{\mathbf{a},i,j}=p(\mathbf{s}'=i|\mathbf{s}=j,\mathbf{a})\) 。实际上这个算子表示在当前状态下,对所有可能动作 \(\mathbf{a}\) 做最优选择,选择使得即时奖励加上未来折扣价值最大的动作。他存在唯一不动点 \(V^{*}\) 对应最优策略,可以证明,这个最优点存在且唯一,并且总是对应着我们的最优策略。
我们采用这个算子更新值函数。现在的问题是如何证明这个算子最终会迭代到最优点,实际上,这个算子是一个压缩映射,即满足:
这里取无穷范数, \(\gamma\in(0,1)\) 也就是说当我们用 Bellman 算子每做一次变化,其两两之间的距离只会越变越小。如上算如果我们取 \(\bar{V} = V^{*}\) ,根据不动点性质有 \(\mathcal{B}V^{*} =V^{*}\) ,此时:
也就说我们最终可以收敛到最优点。
但是在 FVI 算法种,迭代过程实际上采用的是如下更新规则:
其中算子 \(\Pi\) 满足:
\(\Omega\) 是用例如神经网络等方法表示的价值函数。由于采用 Bellman 更新得到的价值函数并不一定在 \(\Omega\) 种,算子实际上在做从价值函数到监督学习所构成的假设类的欧几里得投影。这也是一个压缩算子,也就是说我们额外做了一个压缩过程,直观感受是在欧几里得空间中有任意两点,并将他们投影到一条直线上时,他们的距离变得更近了。
但是不幸的是 \(\Pi\) 和 \(\mathcal{B}\) 并不一定是一个压缩算子,他们是针对不同距离的压缩算子,比如说,Bellman 算子会让你接近最优点,但是此时压缩投影算法会使得你重新回到 \(\Omega\) 空间中,一种极端情况是,压缩投影算法会使你离最优点越来越远。
上面的分析也适用于对于 FQI 算法的分析,在 online Q iteration 算法中,第三步看起来很很像是一个梯度下降,他应当收敛到最优点,但实际上这并不是一个梯度下降,或者说不是朝着某个定义良好的损失函数的梯度下降。这是因为我们利用第二步得到的目标值本身依赖于 \(Q\) 值,因此,更新方向并不是某个真实损失函数关于 Q 的梯度。换句话说,我们并不是在优化一个稳定的目标,而是在拟合一个不断移动、依赖自身的目标函数。这种 bootstrap 的结构虽然高效,但也带来了不稳定性与难以分析的收敛性。当然可以通过某些技术将其转换成收敛的梯度下降,但随着带来的残差算法在实际效果非常糟糕。