k-近邻算法

约 1839 个字 1 张图片 预计阅读时间 12 分钟

k-近邻算法

Important

k-近邻算法中的 k 表示 k 个邻居

k 近邻算法的简单定义：给定一个训练数据集，对新输入实例，在训练数据中找到与该实例最邻近的 \(k\) 个实例，这 \(k\) 个实例的多数属于某个类，就把该输入实例分为这个类。

K近邻算法的三要素

• k 的选择
• 距离度量
• 分类决策规则

k近邻法

输入：训练数据集

\[ T=\left\{ (x_{1},y_{1}),(x_{2},y_{2}),\dots,(x_{N},y_{N}) \right\} \]

其中 \(x_{i}\in \mathcal{X}\subseteq \mathbb{R}^{n}\) 为实例的特征向量，\(y_{i}\in \mathcal{Y}=\left\{ c_{1},c_{2},\dots,c_{K} \right\}\) 为实例的类别，

输出：实例 \(x\) 所属的类 \(y\)

(1) 根据给定的距离度量，在训练集 \(T\) 中找出与 \(x\) 最邻近的 \(k\) 各点，涵盖这 \(k\) 个点的 \(x\) 的领域记作 \(N_{k}(x)\)

(2) 在 \(N_{k}(x)\) 中根据分类决策规则（如多数表决）决定 \(x\) 的类别 \(y\)

\[ y = \underset{ c_{j} }{ \arg \max }\sum_{x_{i}\in N_{k}(x)}^{}I(y_{i}=c_{j}) \]

\(I\) 为指示函数，当 \(y_{i}=c_{j}\) 时 \(I\) 为 1，否则为 0

• 优点

  • 简单易懂：KNN的算法原理非常直观，容易理解和实现。
  • 适应性强：KNN可以用于分类和回归任务，适用于多种类型的数据。
  • 无假设分布：KNN不对数据的分布做出任何假设，能够处理非线性关系的数据。

• 缺点

  • 计算成本高：预测阶段，KNN需要计算新样本与所有训练样本之间的距离。
  • 对噪声敏感：当k值较小时，KNN对噪声数据和异常值较为敏感，因为它是基于局部邻域进行预测的。
  • 需要选择合适的k值：k值的选择对模型性能有显著影响。k值过小可能导致过拟合，k值过大可能导致欠拟合。
  • 样本不平衡问题：当类别分布不均衡时，KNN可能会偏向于多数类，导致对少数类的预测效果较差。

\(k\) 值得选择在 KNN 算法中至关重要，较小的 \(k\) 值意味着整体模型变得复杂，容易发生过拟合；较大的 \(k\) 值意味着模型变得简单

多数表决原则

如果分类的损失为 0-1 损失，分类函数为

\[ f:\mathbb{R}^{n} \to \left\{ c_{1},c_{2},\dots,c_{K} \right\} \]

那么误分类的概率是

\[ P(Y \neq f(X)) = 1-P(Y=f(X)) \]

对给定的实例 \(x \in \mathcal{X}\) ，其最近邻的 \(k\) 个训练实例点构成集合 \(N_{k}(x)\) 。如果涵盖 \(N_{k}(x)\) 的区域的类别是 \(c_{j}\) ，那么误分类是

\[ \frac{1}{k}\sum_{x_{i}\in N_{k}(x)}^{}I(y_{i}\neq c_{j}) = 1-\frac{1}{k} \sum_{x_{i}\in N_{k}(x)}^{}I(y_{i}= c_{j}) \]

要是误分类率即经验风险概率最小，就要使 \(\underset{ x_{i}\in N_{k}(x) }{ \overset{ }{ \sum } }I(y_{i}= c_{j})\) 最大，所以多数表决规则等价于经验风险最小化

我们用距离衡量数据点之间的相似程度，实际上我们也可以用角度来表示其相似程度。

几种距离度量：

• \(L_{p}\) 距离：

\[ L_{p}(x_{i},x_{j}) =\left( \sum_{l=1}^{n} \lvert x_{i}^{(l)}-x_{j}^{(l)} \rvert^{p} \right)^{1/p} \]

• 欧式距离：（\(p=2\)）

\[ L_{2}(x_{i},x_{j}) =\left( \sum_{l=1}^{n} \lvert x_{i}^{(l)}-x_{j}^{(l)} \rvert^{2} \right)^{1/2} \]

• 曼哈顿距离：（\(p=1\)）

\[ L_{1}(x_{i},x_{j}) =\sum_{l=1}^{n} \lvert x_{i}^{(l)}-x_{j}^{(l)} \rvert \]

• \(L_{\infty}\) 距离：（\(p=\infty\)）

\[ L_{p}(x_{i},x_{j}) = \underset{ l }{ \max }\lvert x_{i}^{(l)}-x_{j}^{(l)} \rvert \]

不同的度量会产生不同的结果。当然，我们可以直接学一个度量出来。在机器学习中，对高维数据进行降维的主要目的时希望找到一个合适的低维空间，在此空间中进行学习能比原始空间性能更好，事实上每个空间对了在样本属性上定义的一个距离度量，而寻找合适的空间，实质上就是在寻找一个合适的距离度量。那么为何不直接尝试“学习”出一个合适的度量距离呢？这就是度量学习的基本动机。我们希望学习到的距离度量下，相似对象的距离小，不相似对象间的距离大。

采用马氏距离学习出来的模型：引入马氏距离（Mahalanobis Distance）对欧氏距离做一个修正：

\[ \mathcal{D}(\vec{x}_{i},\vec{x}_{j}) = (\vec{x}_{i}-\vec{x}_{j}) ^{T}M(\vec{x}_{i}-\vec{x}_{j}) \]

其中 \(M\) 是一个半正定矩阵，即 \(M = L^{T}L\)

假定 \(y_{ij}\in \left\{ 0,1 \right\}\) 表示标签 \(i\) 是否匹配标签 \(j\)，用 \(j \rightsquigarrow i\) 表示输入 \(\vec{x}_{j}\) 是输入 \(\vec{x}_{i}\) 的最近邻居

Xing 提出一个度量学习的模型：

Note

在如下条件下：

1. \(\sum_{ij}y_{ij}\mathcal{D}_{M}(\vec{x}_{i},\vec{x}_{j})\leq 1\)
2. \(M \succeq 0\)

最大化 \(\sum_{ij}(1-y_{ij})\sqrt{\mathcal{D}_{M}(\vec{x}_{i},\vec{x}_{j})}\)

Weinberger 引入了松弛变量，提出如下模型：

Note

在如下条件下：

1. \((\vec{x}_{i}-\vec{x}_{l}) ^{T}M(\vec{x}_{i}-\vec{x}_{l})-(\vec{x}_{i}-\vec{x}_{j}) ^{T}M(\vec{x}_{i}-\vec{x}_{j})\geq 1-\xi_{ijl}\)
2. \(\xi_{ijl}\geq 0\)
3. \(M \succeq 0\)

最小化：\((1-\mu)\sum_{i,j\rightsquigarrow i}^{}(\vec{x}_{i}-\vec{x}_{j}) ^{T}M(\vec{x}_{i}-\vec{x}_{j})+\mu \sum_{i,j \rightsquigarrow i,l}^{}(1-y_{il})\xi_{ijl}\)

kNN 面临的挑战：

• k 值确定
• 特征的选择
• 距离函数确定
• 复杂度

k-d 树

Important

k-d 树中的 k 表示 k 个维度

k-d 树是每个叶子节点都为 k 维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点，节点右边的子树代表在超平面右边的点。选择超平面的方法如下：每个节点都与 k 维中垂直于超平面的那一维有关。因此，如果选择按照 x 轴划分，所有 x 值小于指定值的节点都会出现在左子树，所有 x 值大于指定值的节点都会出现在右子树。这样，超平面可以用该 x 值来确定，其法线为 x 轴的单位向量。

k-d 树是二叉树，表示对 k 为空间的一个划分，构造 kd 树相当于不断地用户垂直于坐标轴地超平面将 k 维空间划分，构成一些系列的 k 维超矩形区域，其复杂度为 \(\mathcal{O}(\log N)\)

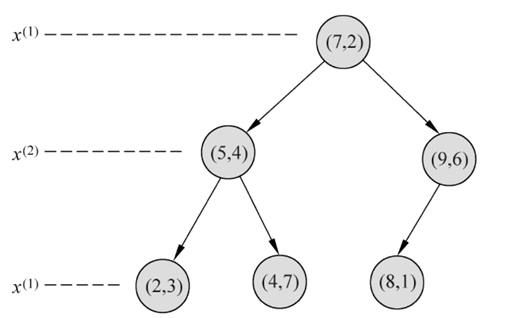
对于深度为 \(j\) 的节点，选择 \(x_{l}\) 为切分坐标，其中 \(l = j(\text{mod } {k})+1\)，以实例中的中位数为切分点（中位数的求取是序列的长度除以2向下取整后的下一个数（升序排序），如，序列长度为7，则中位数为4，长度为8，则中位数为5。）

Example

\[ T= \left\{ (2,3)^{T},(5,4)^{T},(9,6)^{T},(4,7)^{T},(8,1)^{T},(7,2)^{T} \right\} \]

选择 \(x_{1}\) 为切分，中位数为 \(4\) ，取 \(7\) 为第一个节点，进入第一个深度，选择 \(x_{2}\) 为切分，中位数为 \(2\) ，分别选择 \(4\) 和 \(6\) 为节点，依次类推，最后切割结果