单自由度振动

约 2565 个字 8 张图片 预计阅读时间 17 分钟

单自由线性系统

\[ m \ddot{x} +c\dot{x}+kx =F(t) \]

取 \(F(t) = F_0e^{i\omega t}\)，研究其特解。取 \(x(t) = x(s)e^{i\omega t},x(s)\)是一个和自身系统有关的参数，带入方程求解可得

\[ (-m\omega^2+i\omega c+k)x(s) e^{i\omega t}= F_0e^{i\omega t} \]

消去 \(e^{i\omega t}\)，整理得

\[ x(s) = \frac{F_0}{(k-m\omega^2+i\omega c)} \]

记 \(F_0/k = \delta\)也就是振系的零频率扰度（常力作用下的静挠度），对方程整理得，有

\[ \frac{x(s)}{\delta} = \frac{1}{(k-m\omega^2+i\omega c)/k} \]

引入频率比： \(s = \frac{\omega}{\omega_0}\)，对于上述表达式则又有

\[ \frac{x(s)}{\delta} = \frac{1}{1-s^2+2\xi si} \]

定义放大率 \(\beta\) (也就是直接取模)和\(\varphi\) 有

\[\begin{aligned} &\beta(s )=\frac{1}{\sqrt{(1-s^2)^2+(2\xi s)^2}}\\ &\tan \varphi(s)= \frac{2\xi s}{1-s^2} \end{aligned} \]

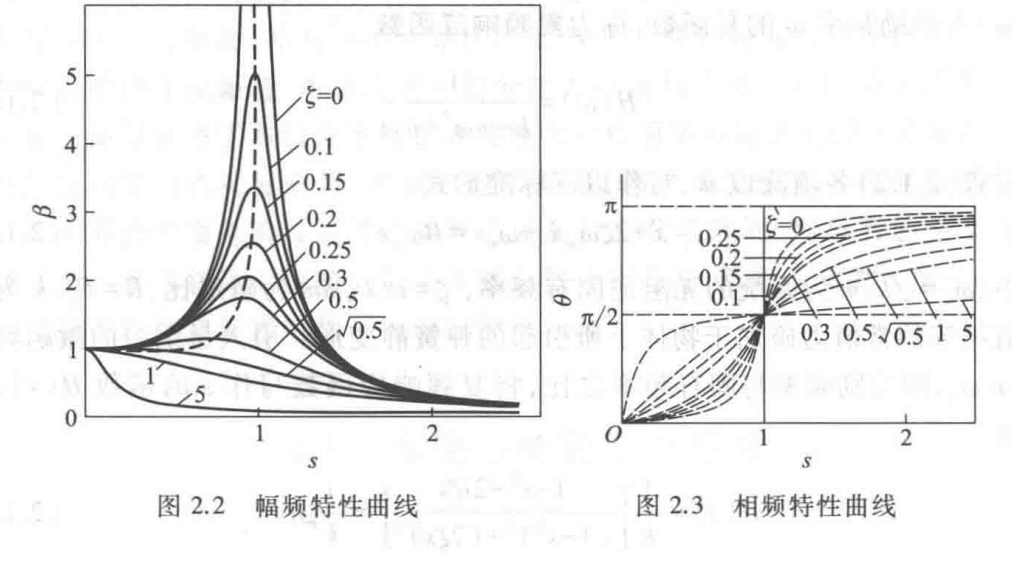
特征：

1. 稳态响应是激励力频率相同的简谐振动
2. 振幅和相位差由系统本身和激励力得物理性质确定，与初始条件无关
3. \(\underset{ s \to {0} }{ \lim }\beta(s)=1,\underset{ s\rightarrow \infty }{ \lim }\beta(s)=0\)，表明激励力频率远小于固有频率时振幅接近弹簧静变形，激励力频率远大于固有频率时振幅趋近零
4. \(\xi = 0,\underset{ s \to {1} }{ \lim }\beta(s)=1\)该现象称为共振，此时激励力频率等于固有频率 \(\omega_{n}\)
5. \(\xi \neq 0\)，将振幅取最大值时的激励频率 \(w_m\)定义为共振频率， \(\omega_m = \omega_n\sqrt{1-2\xi^2}\)，共振区的幅频特性曲线称为共振峰

6. 系统中的阻尼强弱性质和共振峰的陡峭程度可通过振幅放大因子体现，称为品质因数\(Q = \beta|_{s=1} =\frac{1}{2\xi}\) 在共振峰两侧取 \(\beta = Q/\sqrt{2}\)对应两点 \(\omega_1\)和 \(\omega_2\) \(\Delta \omega = \omega_2-\omega_1\)称为系统的带宽，满足 \(\Delta \omega = \frac{\omega_n}{Q}\)

7. 低频受迫振动响应与激励力同相，高频率反相。

对于3和7的一些物理解释 考虑一下矢量图：

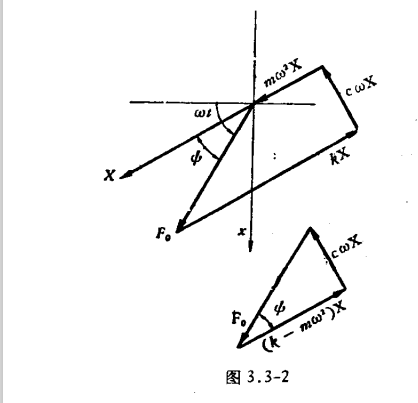
• 当\(\omega\)较小的时候，\(m\omega^2X,c\omega X\)都是小量，可以忽略不记，只剩下恢复力 \(kX\)，其作用结果近似于静挠度，所以辐角较小
• 当\(\omega\)较大的时候，\(m\omega^2X\)较大，惯性力其主导作用，系统保持原有状态，因此振幅接近零，辐角接近惯性力方向（ \(\varphi = \pi\)）
• 当 \(w = w_0\)时，惯性力和恢复力相互抵消，只有阻尼力作用。但是阻尼力作用效果有限，当\(\omega\)略大或略小时，惯性力与恢复力作用效果足以覆盖阻尼力的作用效果

惯性力

考虑\(F(t)= m \omega^2 \sin(\omega t +\varphi)\)，也就是由相对运动引起的振动。

带入上面的方程可得

\[\begin{aligned} &\beta(s) = \frac{s^2}{\sqrt{(1-s^2)+(2\xi s)^2}}\\ & \tan \varphi(s) = \frac{2\xi s}{1-s^2} \end{aligned} \]

大概图像：

多个谐和激励

考虑 \(f(t) = \sum_{i=1}^n A_i \sin(\omega_i \varphi_i)\)，所以对应稳态响应

\[ x= \sum_{i=1}^nX_i(s)e^{i (\omega_i t+\varphi_i)} \]

带入运动方程，令系数相等可以得出

\[ X_n = \frac{1}{k}\beta_nA_n \]

其中 \(\beta_n=\frac{1}{(1-s^2_n)^2+(2\xi s_n)^2},\tan \varphi(s)= \frac{2\xi s_n}{1-s_n^2}\)也就是不同频率比在频率比曲线上所对应的点（将连续化作离散）,也就是说，对于多个谐和激励的振动系统，我们可以先做出系统的幅频特性曲线，根据求得的频率比确定其对应的放大率，进而求得系统的解。

以频率为横坐标，作出 \(\beta_n\)和 \(\varphi_n\)的离散图称为频谱图，可用于分析周期激励力的响应状况，该方法也适用于分析任意周期惯性力激励的受迫振动。

变换解法

Laplace 变换

我们尝试用Laplace变换求解单自由度振动系统，考虑

\[ \ddot{x}+2 \xi \omega_0x + w_0^2x = f(t) \]

作Laplace变换

\[ \left[p^2+2\xi \omega_0p+\omega_0^2\right]\mathcal{L}[x]-2\xi\omega_0 x(0)-px(0)-\dot{x}(0) = \mathcal{L}[f(t)] \]

\[ \mathcal{L}[x] = \frac{\mathcal{L}[f(t)]}{p^2+2\xi\omega_0p+\omega_0^2}+\frac{2\xi\omega_0x(0)+px(0)+\dot{x}(0)}{p^2+2\xi\omega_0p+\omega_0^2} \]

作反演即可得到结果

我们来研究第一项的反演结果，我们先给出反演结果

\[ x(t) = \int^th(\tau-t)f(\tau)d\tau \]

其中 \(h(t)\)是我们所讨论过的单位脉冲载荷。

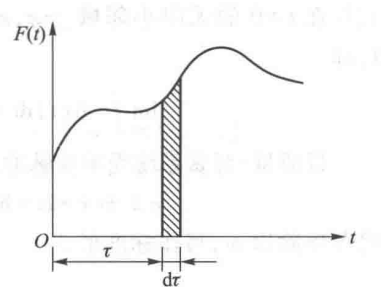
让我们考虑 \(\tau\) 时刻 \(d\tau\)所给出的冲量 \(f(\tau)d\tau\)。如果我们只考虑此时施加的冲量对 \(t\) 时刻产生的影响，即如下运动方程

\[ \ddot{x}+2 \xi \omega_0x + w_0^2x = \delta(t-\tau) f(\tau) d\tau \]

由单位脉冲响应可以给出解

\[ x(t)_{\tau}= h(t-\tau)f(t)=\frac{f(t)}{\sqrt{1-\xi^2}w_0} e^{-\xi\omega_0 (t-\tau)}\sin(\sqrt{1-\xi^2}\omega_0 (t-\tau)) \]

叠加起来就是（线性系统）

\[ x(t) = \int^t_0h(t-\tau)f(\tau)d\tau \]

这个也称杜哈梅积分

实际上，第二项的反演结果是一个指数衰减的波，我们可以不考虑他的作用，同时，当我们的初始条件为静止时，第二项就会自动消失。

Fourier 变换

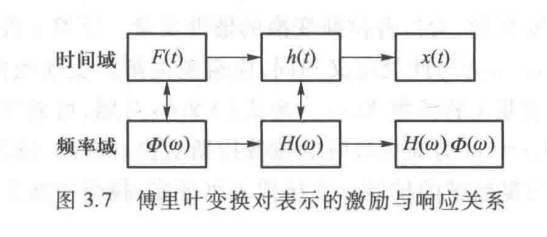
我们也可以用Fourier 变换求解系统运动状态方程

我们已知 \(x(t) = h(t)*f(t)\)（卷积），则可以给出Fourier 变换后位移表达式

\[ X(\omega) = 2\pi H(\omega)\Phi(w) \]

其中 \(H(\omega)=\mathcal{F}(h(t)),\Phi(\omega) = \mathcal{F}(f(t))\)

如果我们只考虑单位脉冲载荷，也即是方程：

\[ \mathcal{F}[\ddot{h}(t)+2\xi \omega_0\ \dot{h}(t)+\omega^2_0] =1 \]

所以我们可以得到

响应谱

如果我们只考虑运动过程中最大振幅，将其与静扰度进行比较我们可以得出位移响应谱

用一个例题讲解，例题细节见教材P76例3.1.2

设质量-弹簧系统在 \((0,t_1)\)时间间隔内受到的矩形脉冲力激励

\[ F(t) = \cases{F_0 \quad (0\le t \le t_1)\\ 0 \qquad(t> t_1)} \]

我们给出解

\[ x(t) = \cases{\frac{F_0}{k}(1-\cos \omega_n t)(0\le t\le t_1)\\ \frac{F_0}{k}[\cos \omega_n(t-t_1)-\cos \omega_n t](t > t_1)} \]

我们可以看出最大振幅响应与 \(t_1\)的选取有关，当 \(t_1\) 比较小时，最大振幅出现在 \(t_1\) 附近，当 \(t_1\) 比较小时，最大振幅出现在 \(\frac{T}{2}\)（半个周期）

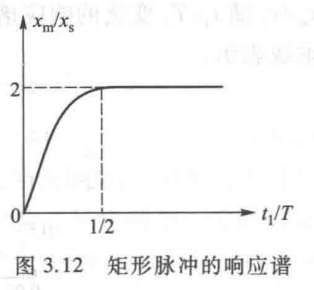
同理我们可以给出速度响应谱和加速度响应谱

随机激励

高斯分布

\[ p(x) = c e^{-\frac{(x-\mu)}{2\sigma^2}} \]

因为能够用相关函数来处理随机激励问题

我们给出位移的自相关函数

\[ R_{xx}[t_1,t_2]= E[x(t_1),x(t_2)] \]

也可以改写成

\[ R_{xx}[t,\tau] = E[x(t),x(t-\tau)] \]

显然这个自相关函数跟初始时间点\(t\)和时间差\(\tau\)有关。但是对于平稳随机过程，我们可以认为自相关函数只与时间差有关，也就是

\[ R(\tau) = E[x(t),x(t+\tau)] \]

我们计算自相关函数的傅里叶变换对可以得到功率谱

\[ S_x(\omega) = \int^{\infty}_{-\infty} R_x(\tau) e^{-i\omega \tau}d \tau \]

\[ R_x(\tau) = \frac{1}{2\pi} \int^{\infty}_{-\infty}S_x(\omega)e^{i\omega \tau}d \omega \]

两个不同平稳随机过程 \(X(t)\) 和 \(Y(t)\) 之间的相关性由互相关函数描述

\[ R_{xy}(\tau) =E[X(t)Y(t+\tau)] \]

考虑平稳响应 \(x(t) = h(t)*f(t)\)

位移自相关函数:

\[ R_{xx} (\tau) = E[x(t_1)x(t_1+\tau)] =E[\int^{t_1}_{0}h(\tau_1)f(t_1-\tau_1)d\tau_1\int^{t_1+\tau}_{0}h(\tau_2)f(t_1+\tau-\tau_2)d\tau_2] \]

可以得到位移功率谱与激励功率谱关系

\[ S_{xx}(\tau) = \int^{\infty}_{-\infty} R(\tau)e^{i \omega t}d\tau =H(\omega)H^*(\omega)S_{ff}(\omega) = |H(\omega)|^2S_{ff}(\omega) \]

高斯白噪声：空间域上符合高斯分布，白噪声：相关函数为0（不相关）

广义单自由度

我们之前所研究的单自由度振动系统都是在忽略弹簧质量的情况进行研究的，此时弹簧质量 \(m\) 和物体质量 \(M\) 满足 \(M\gg m\)，但当我们考虑弹簧质量时，此时我们仍能将其视作一种单自由度系统，称为广义单自由度系统。

考虑以下这种情况：

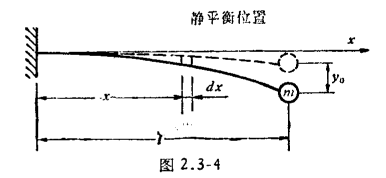
假定弹簧长度 \(l\) 和密度 \(\rho\) 满足线性关系，且 \(l \cdot \rho = m\)，其中 \(m\) 为弹簧的质量。假定弹簧与物体连接处速度为 \(\dot{x}\)，另一端固定，同时假定弹簧上速度线性分布，因此可以给出离原点\(y\)处的弹簧微段速度方程

\[ dT = \frac{1}{2}(\rho dy)(\dot{x}\frac{y}{L})^2 \]

积分得

\[ T = \int_0^L \frac{1}{2}(\rho dy)(\dot{x}\frac{y}{L})^2 = \frac{1}{6}\rho L \dot{x}^2 = \frac{1}{6}m\dot{x}^2 \]

这样我们就可以给出系统中动能和势能（势能只由弹簧的变形引起）

\[ T =(\frac{1}{6}m+\frac{1}{2}M)\dot{x}^2,\quad V = \frac{1}{2}kx^2 \]

然后通过Lagrange函数便可解出系统运动方程

因此，对于质量无法忽略的弹性元件，我们可以给出弹性元件的速度分布

\[ \begin{aligned} &z =\dot{x}w(y)\\ &w(y_0) = 1 \end{aligned} \]

\(y_0\)为弹性元件与物体的接触位置， \(w(y)\)与弹性元件的质量分布和变形方式有关

例如，对于悬臂梁，材料力学的知识可以给出

\[ w(y) = \frac{3lx^2-x^3}{2l^3} \]

等效刚度

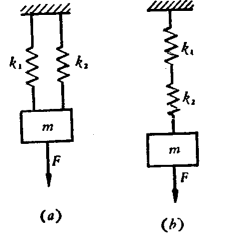
我们先考虑两个弹簧的串并联问题

对于串联弹簧，他们此时受的力是相同的，对于单位作用力有

\[ x_1= \frac{1}{k_1} ,\quad x_2 =\frac{1}{k_2} \]

此时对等效弹簧仍有关系式

\[ x= \frac{1}{k} \]

所以等效刚度

\[ \frac{1}{k} = \frac{1}{k_1}+\frac{1}{k_2} \]

对于并联弹簧，他们此时因外力引起的位移是相同的，对于单位位移有

\[ F_1 = k_1 \cdot1,\quad F_2= k_2\cdot1 \]

此时对等效弹簧仍有关系式

\[ F =k\cdot1 \]

所以等效刚度

\[ k = k_1+k_2 \]

Notes

这边举几个常见的等效弹簧的例子