Policy Gradients

约 3947 个字 2 张图片 预计阅读时间 26 分钟

Slides

部分笔记参考: CS285课程笔记（3.1(1)）——Model-free方法之Policy Gradient - 知乎

Policy Gradients

策略梯度是强化学习中最简单的算法之一，它直接对强化学习目标进行微分 ，然后对策略参数进行梯度下降以改进策略。

如果策略是由深度神经网络表示的，那么 \(\theta\) 表示策略的参数，即神经网络的权重，网络以状态或观察为输入，输出为动作，新状态由转移概率决定，这些概率取决于当前状态和策略产生的动作。

轨迹分布

\[ \underbrace{p_\theta(s_{1},a_{1},\dots,s_{T},a_{T})}_{p_{\theta}(\tau)}= p(s_{1})\prod_{t=1}^{T}{\pi_{\theta}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t}) } \]

我们通常假设不知道给定 \(s_{t},a_{t}\) 时对应的 \(s_{t+1}\) 的转移概率，也不知道初始概率。我们只假设我们可以与现实世界互动，尽管这实际上是从概率分布采样的。

我们有一个奖励函数，取在给定轨迹情况下奖励函数和的期望，并希望能够找到最大化这个期望的参数 \(\theta\) ，即

\[ \theta ^{*} =\underset{ \theta }{ \arg \max }\mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t }^{} r(s_{t},a_{t}) \right] \]

我们提到了根据期望的线性，可以将求和从期望中提出来，然后将期望表示成一个边缘期望，从而定义了有限时域的期望和无限时域的期望，我们先研究有限时域的期望。

我们定义如下函数

\[ J(\theta) = \mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t }^{} r(s_{t},a_{t}) \right] \]

这是用来评估我们模型表现，因为我们假设在现实世界中运行我们的策略 ，相当于从初始状态分布和转移概率中进行采样，我们可以将展开成如下形式：

\[ J(\theta) \approx \frac{1}{N} \sum_{i}\sum_{t}^{} r(s_{i,t},a_{i,t}) \]

\(\underset{ i }{ \overset{ }{ \sum } }\) 表示对 \(\pi_{\theta}\) 中的样本求和，简而言之就是运行我们的策略 \(n\) 次，可以收集到 \(n\) 个轨迹样本，我们通过将每个样本轨迹的奖励求和后取平均，得到对期望无偏估计，理论上 \(n\) 越大我们对这个期望的估计越准确。

我们的问题现在是要在不知道初始概率和转移概率的情况下估计梯度。我们知道可以将期望表示成如下形式：

\[ J(\theta) =\mathbb{E}_{\tau\sim p_{\theta}(\tau)}[r(\tau)] = \int p_{\theta}(\tau)r(\tau)d \tau \]

也就是对概率密度的一个积分（这是因为 \(\tau\sim p_{\theta}(\tau)\) ），考虑一个特性：

\[ p_{\theta}(\tau)\nabla_{\theta}\log p_{\theta}(\tau) = p_{\theta}(\tau)\frac{\nabla_{\theta}p_{\theta}(\tau)}{p_{\theta}(\tau)} = \nabla_{\theta} p_{\theta}(\tau) \]

所以

\[ \nabla J_{\theta}(\theta) = \int \nabla_{\theta}p_{\theta}(\tau)r(\tau)\mathrm{d}\tau = \int p_{\theta}(\tau)\nabla_{\theta}\log p_{\theta}(\tau)r(\tau)\mathrm{d}\tau = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[\nabla_{\theta}\log p_{\theta}(\tau)r(\tau)] \]

考虑 \(\log p_{\theta}(\tau)\) 的表达式：

\[ \log p_{\theta}(\tau) = \log p(\mathbf{s}_{1})+\sum_{t=1}^{T}\log \pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t}) + \log p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t}) \]

由于我们是对 \(\theta\) 求梯度，而初始概率和转移概率都于 \(\theta\) 无关，所以可以写成：

\[ \nabla_{\theta}J(\theta) = \mathbb{E}_{\tau\sim p_{\theta}(\tau)}\left[ \left( \sum_{t=1}^{T}\nabla_{\theta}\log \pi_{\theta}(\mathbf{a_{t}|\mathbf{s_{t}}}) \right) \left( \sum_{t=1}^{T}r(\mathbf{s}_{t},\mathbf{a}_{t}) \right) \right] \]

离散化后：

\[ \nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left( \sum_{t=1}^{T}\nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \right)\left( \sum_{t=1}^{T} r(\mathbf{s}_{i,t}|\mathbf{a}_{i,t}) \right) \]

最后

\[ \theta \leftarrow\theta +\alpha \nabla_{\theta}J(\theta) \]

Reinforce algorithm

1. sample \(\{\tau^i\}\) from \(\pi_{\theta}(\mathbf{a}_t|\mathbf{s}_t)\) (run the policy)
2. \(\nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left( \sum_{t=1}^{T}\nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \right)\left( \sum_{t=1}^{T} r(\mathbf{s}_{i,t}|\mathbf{a}_{i,t}) \right)\)
3. \(\theta \leftarrow\theta +\alpha \nabla_{\theta}J(\theta)\)

将梯度下降法和最大似然进行比较，最大似然目标就是最大化观测动作中的对数概率

\[ \nabla_{\theta} J_{ML}(\theta) \approx \frac{1}{N}\sum_{i=1}^{N}\left( \sum_{t=1}^{T}\nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \right) \]

在最大似然中，我们假定输出的动作是应该采取的最好动作，但是在策略梯度中这件事可能没有办法做到（因为我们前面的策略无法满足我们的要求），因此最大似然只是简单的提高所有动作的对数概率，而策略梯度会跟据每个动作的奖励值提高或者降低这些对数概率，可以视其为最大似然的加权版本。

直观上理解策略梯度法：执行一些轨迹并计算它们的奖励，其中有些有正奖励，一些有负奖励，你想要做的是，沿着好的轨迹增加它们的对数概率，沿着坏的轨迹降低它们的对数概率，我们希望好的事情更能发生，而坏的事情不容易发生。

我们知道，状态(state)满足马尔可夫性质，而观测(observation)并不满足，但在推导策略梯度的过程中，我们实际上并没有用到马尔可夫性质，因此，对于部分可观测的系统推导策略梯度，我们依旧可以重复之前的做法，并且我们依旧能得到相同的结果。

但是这个方法有一个问题就是方差会很高：

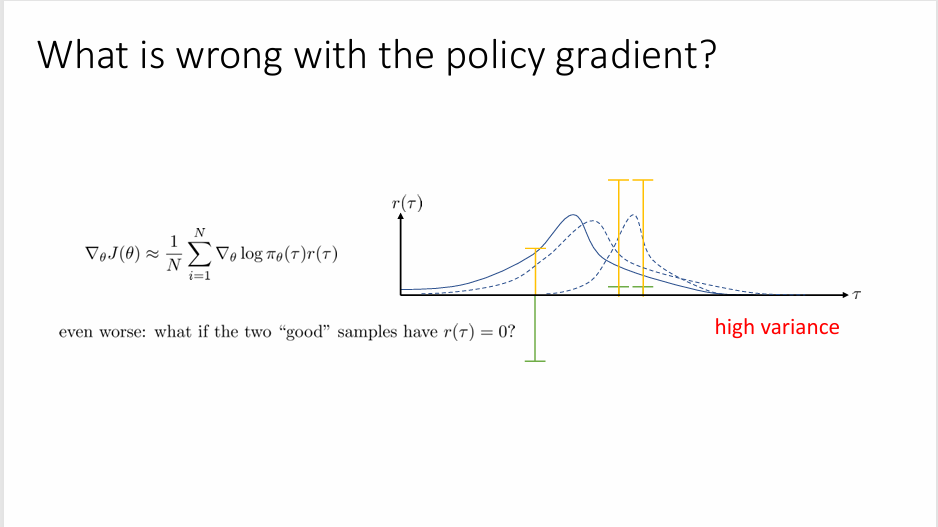
这里横坐标代表不同的采样样本，绿色线段是采样得到的智能体与环境交互后得到的奖赏值；第二步向第一步得到的奖赏值上加一个常量，该常量并不会影响策略梯度（下文也有相关推导）。但这两次得到的策略的概率分布结果却相差很多，这就是策略梯度方法高方差问题的直观体现，而高方差带来的问题就是算法更新的过程不稳定。

所以我们需要解决这个问题。

第一个方式进行 Causality 的假设，也称因果假设，简而言之就是你现在的行为不会改变过去获得的奖励（过去的奖励与现在的决策是独立的）

我们将根据每个时间步的行动是否对应于当前和未来的更大的奖励，但也在过去来改变该时间步行动的对数概率，然而我们知道时间步 \(t\) 的行动不能影响过去的奖励，这意味着这些其他奖励必然会在期望中抵消，这意味着如果我生成足够多的样本，最终我们应该看到所有时间步 \(t'\) 小于 \(t\) 的奖励平均下来会乘以零，它们不会影响这个时间步的对数概率，所以策略梯度的估计式可以修改为如下形式：

\[ \nabla_{\theta}J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N}\Bigg[ \Big( \sum_{t=1}^{T}\nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})\Big) \Big( \underbrace{\sum_{t'=t}^{T}r(\mathbf{s}_{i,t},\mathbf{a}_{i,t}) }_{\hat{Q}(i,t)}\Big) \Bigg] \]

修改后的奖赏值这一部分又被称为"reward to go"，可以表示为 \(\hat{Q}(i,t)\) ，直观理解就是只考虑从当前策略的时间往后推移的奖赏值，而不考虑之前的。

第二个方法使在奖赏值的基础上减去一个常数。如果我们好的轨迹对应正的奖励；坏的轨迹对应坏的奖励，那么策略梯度是一个还不错的方法，但会遇到这种情况：坏的轨迹也会对应正的奖励，尽管奖励值加上或减去一个常数不会影响比较高奖励值的位置，但多多少少都会影响我们的后面的策略。

\[ \nabla_{\theta}J(\theta) = \mathbb{E}[\nabla_{\theta}\log p_{\theta}(\tau)(r(\tau)-b)] \]

离散化：

\[ \nabla_{\theta}J(\theta) =\frac{1}{N} \sum_{i=1}^{N} \nabla_{\theta}\log p_{\theta}(\tau)(r(\tau)-b) \]

最简单情况下的baseline取值为 \(b = \frac{1}{N}\sum_{i=1}^{N}r(\tau)\) ，这不是最优的选择，但是足够有效。

但是我们需要考虑baseline是否会想到原来的策略梯度，也就是是否会引入bias：

\[ \mathbb{E}[\nabla_{\theta}\log p_{\theta}(\tau)b] = \int p_{\theta}(\tau)\nabla_{\theta}\log p_{\theta}(\tau)b=\int \nabla_{\theta}p_{\theta}(\tau)b d \tau = b \nabla_{\theta} \int p_{\theta}(\tau)d\tau = b\nabla_{\theta}1 =0 \]

可以看出baseline并不影响策略梯度的精确度。

最优的baseline：

\[ b = \frac{\mathbb{E}[g(\tau)^{2}r(\tau)]}{\mathbb{E}[g(\tau)^{2}]} \]

测量梯度是典型的在线策略算法（on-policy），这是因为每次修改策略时，它们都需要生成新的的样本。在 Policy Gradient 中，我们计算期望的方法是通过使用最新的策略来采样，但是样本的分布与 \(\theta\) 有关，也就意味着，每次更新 \(\theta\) 后，样本的分布发生了改变，我们需要丢掉我们原本的样本。但是在深度学习中，这并不是什么过于严重的问题，因为神经网络在每次梯度步骤中只会发生微小的变化，这是由于神经网络的非线性，我们不能计算大梯度，只能用重复计算大量的小梯度。

这并不意味着Policy Gradient不是一个好方法，我们只是在考虑一种情况：如果采样的代价非常高，比如你在一个昂贵的模拟器中运行你的策略，Policy Gradient 的性价比会变得非常的低。

一个改进的方法就是利用 important sampling

\[\begin{align} \mathbb{E}_{x \sim p(x)}[f(x)] &= \int p(x)f(x) dx \\ &= \int \frac{q(x)}{q(x)}p(x)f(x)dx \\ &= \int q(x)\frac{p(x)}{q(x)}f(x)dx \\ &=\mathbb{E}_{x \sim q(x)}\left[ \frac{p(x)}{q(x)}f(x) \right] \end{align} \]

这种方法使我们可以利用从 \(\bar{p}(\tau)\) 中采样的样本， \(\bar{p}(\tau)\) 可能是之前的一些样本。目标函数就变成了：

\[ J(\theta')= \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \frac{p_{\theta'}(\tau)}{p_{\theta}(\tau)}r(\tau) \right] \]

这里我们用 \(p_{\theta}(\tau)\) 表示旧策略，\(p_{\theta'}(\tau)\) 表示新策略，其梯度为

\[ \nabla_{\theta'}J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \frac{\nabla_{\theta'}p_{\theta'}(\tau)}{p_{\theta}(\tau)}r(\tau) \right] = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_{\theta}(\tau)}\nabla_{\theta'}\log p_{\theta'}(\tau) r(\tau) \right] \]

考虑 \(p_{\theta}(\tau)\) 的表达式 \(p_{\theta}(\tau)=p(s_{1})\prod^{T}_{t=1}\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\) ，因为对于新旧策略，由于初始状态和转移概率是相同的，所以可得到：

\[ \frac{p_{\theta}(\tau)}{p_{\theta'}(\tau)} = \frac{\prod^{T}_{t=1}\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})}{\prod^{T}_{t=1}\pi_{\theta'}(\mathbf{a}_{t}|\mathbf{s}_{t})} \]

将以上的 ratio 表达式进一步带入梯度表达式完全展开可得

\[ \nabla_{\theta'}J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \left( \frac{\prod^{T}_{t=1}\pi_{\theta'}(\mathbf{a}_{t}|\mathbf{s}_{t})}{\prod^{T}_{t=1}\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})} \right)\left( \sum_{t=1}^{T}\nabla_{\theta'}\log \pi_{\theta'}(\mathbf{s}_{t}|\mathbf{a}_{t}) \right) \left( \sum_{t=1}^{T}r(\mathbf{s}_{t},\mathbf{a}_{t}) \right) \right] \]

进一步考虑因果效应

\[ \nabla_{\theta'}J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=1}^{T}\nabla_{\theta'}\log \pi_{\theta'}(\mathbf{s}_{t}|\mathbf{a}_{t}) \left( \prod^{T}_{t'=1}\frac{\pi_{\theta'}(\mathbf{a}_{t'}|\mathbf{s}_{t'})}{\pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t})} \right)\ \left( \sum_{t'=t}^{T}r(\mathbf{s}_{t'},\mathbf{a}_{t'}) \left( \prod^{t'}_{t''=t} \frac{\pi_{\theta'}(\mathbf{a}_{t''}|\mathbf{s}_{t''})}{\pi_{\theta}(\mathbf{a}_{t''}|\mathbf{s}_{t''})}\right) \right) \right] \]

这里对数候的连乘项表示未来的策略，它并不能影响现在策略的参数，如果省略 \(r\) 之后大的连乘项，我们就得到了 Policy iteration 的算法。

我们希望能够使用自动微分来计算策略梯度。如果我们正常地计算梯度，效率可能会比较低，这是因为神经网络内部有大量的参数（参数的数量远大于我们的样本数量），这是非常昂贵的。因此，我们常常运用反向传播，也就是先计算损失的导数，然后利用反向传播将其通过神经网络反向传播（这就是自动微分会做的事情。）利用自动微分，我们只需要定义一个目标函数（或者说损失函数），库会自动根据这个目标函数计算出关于参数的梯度，从而简化了梯度计算过程，并提高了计算效率。

通常情况下，我们利用最大似然估计计算我们的奖赏值和其对应的梯度：

\[ \nabla_{\theta}J_{\mathrm{ML}}(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta}\log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \]

\[ J_{\mathrm{ML}}(\theta) \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \]

我们知道，样本数量 \(N\) 远小于网格参数，因此上述方法没有办法充分利用每个样本中奖励信息的权重信息，只是简单地计算对数概率的梯度。

为了高效利用自动微分包，我们并不是实现 \(J\) 的最大似然估计，而是实现一个称为伪损失(pesudo-loss)的加权似然函数估计：

\[ \tilde{J}(\theta)\approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \log \pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t}) \hat{Q}_{i,t} \]

使用策略梯度时的注意点： - 策略梯度含有高方差 - 使用更大的批次 - 调整学习率更困难 - 更多的超参数调整

考虑一个一维数轴，目标点在原点，而你目前在原点左侧，对应的奖励函数可以写成如下形式：

\[ r(\mathbf{s}_{t},\mathbf{a}_{t} ) = -\mathbf{s}^{2}_{t}-\mathbf{a}^{2}_{t } \]

策略函数：

\[ \log \pi_{\theta}(\mathbf{a}_{t}|\mathbf{s}_{t}) = - \frac{1}{2\sigma^{2}}(k\mathbf{s}_{t}-\mathbf{a}_{t})^{2} + \mathrm{const} \]

参数有两个 \(\theta=(k,\sigma)\) 。这是一个高斯分布，所以你的策略实际上是一个带有噪音的随机游走。

当我们采用梯度方法取优化我们的策略的时候会发现随着 \(\sigma\) 的减小，其对应的梯度增大（这是因为此时 \(\sigma\) 在分母且在策略函数中是一个二次方的项），所以当我们归一化我们的梯度的时候，\(\sigma\) 的影响会占主导地位，于是我们花了大量的时间在优化 \(\sigma\) ，对于 \(k\) 的优化比较少，这会导致效率的降低。这是一个条件不良的问题

我们希望对较大的梯度配备较小的学习率，对较小的梯度配备较大的学习率。我们引入一阶梯度上升：

\[ \theta \leftarrow \arg \max_{\theta'}(\theta'-\theta)^{T}\nabla_{\theta}J(\theta) \, \mathrm{s.t} \, \lVert \theta'-\theta \rVert^{2}\leq\varepsilon \]

但实际上在参数空间上的优化并不等同于在策略空间的优化，因为有些参数的巨大变化对策略的改变较小，而有些参数的微小变换可能引起策略的极大改变。所以我们想要以某种方式重新参数化整个过程，使那些大幅改变策略的参数获得较小的速率；微小改变策略的参数获得较大的速率。

所以我们采用如下迭代方式：

\[ \theta \leftarrow \arg \max_{\theta'}(\theta'-\theta)^{T}\nabla_{\theta}J(\theta) \, \mathrm{s.t} \, D(\pi_{\theta'},\pi_{\theta})\leq\varepsilon \]

\(D\) 是某种散度，比如说 KL 散度。

\[ D_{\mathrm{KL}}(\pi_{\theta'}||\pi_{\theta}) \approx(\theta'-\theta)\mathbf{F}(\theta'-\theta) \]

\(\bf F\) 称为Fisher information 矩阵：

\[ \mathbf{F}= \mathbb{E}_{\pi_{\theta}} [\nabla_{\theta}\log \pi_{\theta}(\mathbf{a|s})\nabla_{\theta}\log \pi_{\theta}(\mathbf{a|s})^{T}] \]