Model-Based Reinforcement Learning
约 4121 个字 1 张图片 预计阅读时间 27 分钟
笔记参考:CS285 深度强化学习 (9): Model-Based Reinforcement Learning - 知乎
如果我们知道模型:\(f(\mathbf{s}_{t},\mathbf{a}_{t})=\mathbf{s}_{t+1}\) (随机情况为 \(p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\) ),那么就可以使用[[Optimal Control and Planning]]的方法控制系统,而不必使用 model-free 方法。因此,如果我们能从数据中将模型学出来,就可以采用规划或者最优控制等方法。
考虑一个简单的算法:
model-based RL version 0.5
- 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\), 收集 \(\mathcal{D}=\left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)
- 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 来最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert\)
- 依据 \(f(\mathbf{s},\mathbf{a})\) 来进行规划
实际上这是经典机器人学中系统辨识(system identification)的工作原理。在使用这种方法时需要一个好的基础策略,其能帮助探索系统的不同模式。这种做法使我们能够在基于先验知识来设定所需要参数时设置较少的参数来提高效率。
但是这种方法不适合像深度学习这样具有高表达能力的模型,因为这些模型会更精确的拟合数据中看到的特定分布。一个例子是我们正在训练一个爬山的模型,我们选择的基础策略 \(\pi_{0}(\mathbf{s}_{t})\) 为随机行走,训练结果告诉我们往右走的结果是海拔升高。于是在接下来的规划中,策略 \(\pi_{f}\) 告诉我们一直朝右走,然后从山顶掉下去(这是一个很糟的情况),这个问题的原因正是在模仿学习中讨论过的 Distribution shift(mismatch),也就是
规划中的策略 \(\pi_{f}(\mathbf{s}_{t})\) 使我们有更高的可能进入那些 \(\pi_{0}\) 低概率出现的状态,于是在这些状态,我们的模型给出的错误预测并选择错误的“最优”动作,然后进入下一个状态做出更错误的预测。
一个改进方法是借鉴 DAgger 的思想(实际上这个方法出现比 DAgger 早):收集额外的数据来调整策略。我们可以选择特定的状态和动作,然后观察下一个状态。这意味我们能收集到更多的数据。:
model-based RL version 1.0
- 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\), 收集 \(\mathcal{D}=\left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)
- 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 来最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert\)
- 依据 \(f(\mathbf{s},\mathbf{a})\) 来进行规划
- 利用 \(\pi_{f}\) 收集新的数据,更新 \(\mathcal{D}\) ,重复 2-4
可以进一步改进我们的算法:在模型犯错时立即修正,而不是等着模型更新,这样可以让学习速度更快,也就是在犯错时重新规划我们的行为,并纠正错误。
model-based RL version 1.0
- 运行 base policy \(\pi_{0}(\mathbf{a}_{t},\mathbf{s}_{t})\), 收集 \(\mathcal{D}=\left\{ (\mathbf{s},\mathbf{a},\mathbf{s}')_{i} \right\}\)
- 学习 dynamic model \(f(\mathbf{s},\mathbf{a})\) 来最小化 \(\sum_{i}\lVert f(\mathbf{s}_{i},\mathbf{a}_{i})-\mathbf{s}_{i}' \rVert\)
- 依据 \(f(\mathbf{s},\mathbf{a})\) 来进行规划
- 执行第一个规划的 action ,观测到新的状态 \(\mathbf{s}'\)
- 添加 \((\mathbf{s},\mathbf{a},\mathbf{s}')\) ,更新 \(\mathcal{D}\) ,重复 3-5;每 \(N\) 次回到 2.
这个方法也称模型预测控制(Model Predictive Control MPC)。着个过程更能容忍模型犯的错误。
因为在训练过程中总是需要重新规划,因此随着规划的次数的增加,每次规划就不需要做到特别完美,我们允许在每次规划中犯更多的错误,这是因为下次规划会修正这些错误,因此我们可以采用更短的 horizon ,随机采样方法也可以起效。
Uncertainty in Model-Based RL
不确定性在基于模型的强化学习中扮演着非常重要的角色。
一个问题是, 在 model-based 与 model-free 之间存在着一个性能差异:虽然在开始时, model-based 很容易就得到了一个正的奖励,而 model-free RL 通常起始时是很大的负值。然而在经过训练后,model-based 的奖励可能会陷入一个较低的值,而 model-free 的性能可能显著超过 model-based。
这个问题的原因是,在开始样本量比较少的时候,我们既要避免过拟合,还需要足够的容量在样本量增大时能够表现良好,这并不是一件容易的事情。我们通过使用模型收集额外数据来缓解分布偏移问题,这要求模型在样本量少的时候性能要好;但是而神经网络这样的高容量模型在小数据量的情况下容易产生过拟合,高容量模型在小样本情况下表现差,低容量模型在大样本情况下表达不足;结果就是策略性能在某个水平上始终爬升缓慢,甚至陷入“停滞”。
这可以总结成过拟合+分布偏移的问题
不确定性是不仅预测了下一个状态,还预测了下一个状态可能的分布,考虑走到悬崖边上,尽管越靠近悬崖得到的奖励越高,但是伴随着的是悬崖的风险(高负收益),不确定性会使你自动保持一定距离(因为你不知道悬崖的确切的位置)。我们并没有特意避免最坏情况,我们只是在不确定的模型下对奖励的期望值进行推理,避免那些可能会对奖励产生负面的高度不确定的区域(但此时并不只是在最大化期望回报),这件事实际上是一种风险对冲,它迫使规划器采取一系列预期良好的动作。对不确定性的建模需要考虑到处在可能的世界,这并不是系统本身存在噪声的情况,而是不确定系统是什么的情况。有很多可能的世界与数据一致,而你采取的动作在这些可能的世界里的预期是好的。不过这只是一种特殊的不确定性情况
所以只需要修改原始算法的第三点:只采取会带来高期望奖励函数的行动。
注意事项:
- 需要探索以获得更好的结果。(不能因噎废食)
- 期望值并不等同与悲观的结果。
- 期望值也不等同与最好的结果。
Uncertainty-Aware Neural Net Models
获得感知不确定模型的一种方法是用输出分布的熵,但这是一个糟糕的想法。
一般而言,不确定性分为两种:
- Aleatoric(statistical) Uncertainty: 这里的不确定性是来源于数据的,可以视作是噪声或者数据本身的不确定性,不随数据量的增加而改变。
- Epistemic(model) Uncertainty: 这里的不确定性是源自于对模型的不了解。当收集到足够数据时,这种不确定性就会消失。
因为熵是用于衡量信息量的方法,因此如果我们想要一个熵比较低的模型,那么损失函数就会逼迫模型做出极为自信的结果,但是熵无法分辨上面两种不确定性,这就会导致他做出错误判断时仍保持高度自信。
一种方法是对模型的不确定性做出预测,这是在模型对数据有把握,但对模型没有把握的情况,假定模型满足分布 \(p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\) 我们需要做的就是估计参数 \(\theta\) 。一般而言,我们需要估计参数的后验分布,假设先验概率 \(p(\theta)\) 均匀分布,就能得如下等式
第一个等式是极大似然的结果,因此我们转而估计 \(\log p(\theta|\mathcal{D})\) ,这件事的好处是他的熵告诉我们模型对参数的不确定性,做:
但是这要求对所有参数进行积分,这是一件无法做到的事情。因此需要求助其他的近似方法。
一种近似方法是借助贝叶斯神经网络。在贝叶斯神经网络中,每一个权重都有一个分布,在最一般的情况下存在所有权重的一个联合分布。但是对参数的完整联合分布进行建模非常困难,因为参数是高维的。一种方法是估计参数后验:
也就是参数之间是独立的,但这并不是一个很好的近似方法,因为一般而言参数之间具有非常紧密的相互作用效应,但是简单且易于处理。假定每个参数满足高斯分布:\(p(\theta_{i}|\mathcal{D})=\mathcal{N}(\mu_{i},\sigma_{i})\) ,\(\mu_{i}\) 表示权重的期望,\(\sigma_{i}\) 表示关于权重的不确定性。
另一个有效的方法是 Bootstrap ensembles 。这个思想是,与其训练一个神经网络来预测状态的分布,不如训练多个不同的神经网络,并且使其多样化,在理想情况下,它们在训练数据上都会表现得相似且准确,但在训练数据之外,会犯不同的错误。于是将这些神经网络整合起来,并让它们为下一个可能的状态投票。
预测时:
我们混合的是概率,而不是预测,如果参数满足高斯分布,我们并不是将不同参数的均值平均化,而是做了一个高斯混合模型。
每个模型都需要在独立于其他模型数据集却来自同一个分布的数据集上进行训练。一个简单方法是将数据划分成 \(n\) 份不重叠的数据集,但这是一个比较浪费的方法。另一个方法是采用有放回的采样来生成 \(\mathcal{D}_{i}\)
在深度学习中 Bootstrap ensembles 方法也能其效果,不过这是一个非常粗糙的近似,因为模型的数量太少了(因为代价非常高,数量一般小于 \(10\)) 。不过我们并不需要重新采样,因为 SGD 和随机初始化这两件事已经使得模型之间表现出一定的差异。
在引入不确定度之前,我们的优化问题是:
现在我们有了 \(n\) 个可能的模型,并希望最大化所有模型上的平均奖励
对于候选的动作序列 \(\mathbf{a}_{1},\dots,\mathbf{a}_{H}\) ,考虑一下几步:
- 采样 \(\theta \sim p(\theta|\mathcal{D})\),相当于随机选择一个模型
- 在每个时间步上,采样 \(\mathbf{s}_{t+1}\sim p(\mathbf{s}_{t}|\mathbf{s}_{t},\mathbf{a}_{t},\theta)\)
- 计算 \(R= \sum_{t}r(\mathbf{s}_{t},\mathbf{a}_{t})\)
- 重复计算 1-3 步来计算平均的奖励。
这只是一种用于评估奖励的采样程序,并不是唯一方法。
Model-Based RL with Images
之前讨论的算法有一个共同特点:拥有某种形式的模型,能够根据先前的状态和动作预测下一个状态,并在这些状态上规划。但是对于图像问题,图像一般是高维数据,这使得预测变得困难;图像包含大量冗余数据。基于图像的任务往往具有部分可观测性,也就是说当你之观察游戏中某一个画面,你无法知道游戏中的球运动速度有多快,或者朝哪个方向上运动。因此处理图像是,我们通常会涉及部分可观测马尔可夫决策过程 。通常在用图像进行强化学习时,我们知道观测和动作,但不知道状态。
基于图像的强化学习一个思想是我们能否分开学习 \(p(\mathbf{o}_{t}|\mathbf{s}_{t})\) 和 \(p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\) ,这样做的好处是第一个分布处理了高维的问题,而第二个分布处理了dynamics的问题 。这样的模型称为状态空间模型,有时也被称为潜在空间或潜在状态模型。
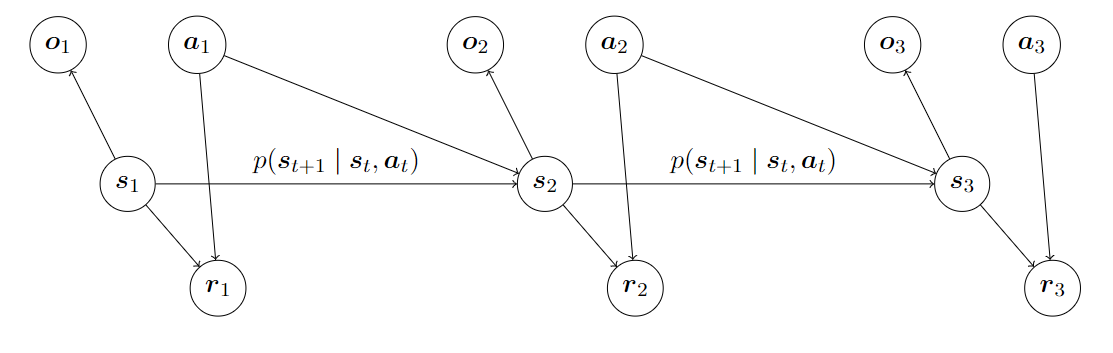
在这个过程中我们一共要学习三个模型:
- observation model:\(p(\mathbf{o}_{t}|\mathbf{s}_{t})\)
- dynamics model:\(p(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\)
- reward model:\(p({r}_{t}|\mathbf{s}_{t},\mathbf{a}_{t})\)
对于标准(全观察)模型,我们采用最大似然函数的方法来训练,但在潜在空间模型中,考虑到观察的影响,选择如下似然函数:
但问题是对于状态并没有一个合适的模型,所以我们需要一个算法能够估计状态的后验分布,并从该近似后验分布中采样状态来估计似然函数。因此,对如下状态做期望 \((\mathbf{s}_{t},\mathbf{s}_{t+1})\sim p(\mathbf{s}_{t},\mathbf{s}_{t+1}|\mathbf{o}_{1:T},\mathbf{a}_{1:T})\)
采用神经网络来近似后验分布:\(q_{\psi}(\mathbf{s}_{t}|\mathbf{o}_{1:t},\mathbf{a}_{1: t})\) ,得到的模型称为编码器(encoder),近似后验分布有很多种选择:全面平滑后验分布 \(q_{\psi}(\mathbf{s}_{t},\mathbf{s}_{t+1}|\mathbf{o}_{1:t},\mathbf{a}_{1: t})\) ,这个后验分布给了精确的预测量,但是比较难学习;另一个极端为 \(q_{\psi}(\mathbf{s}_{t}|\mathbf{o}_{t})\) ,称为单步编码器。这是最容易训练的后验分布,但也是最糟糕,因为他离真实的后验分布最远。当可以从当前观测中预测出状态时,单步编码器是一个不错的选择。
如果只考虑简单的确定性的情况,encoder 表示为:
我们的目标就是在所有轨迹中使 \(\phi\) 和 \(\psi\) 最大化:
利用反向传播来联合优化 \(\phi\) 和 \(\psi\) ,如果考虑奖励模型,则:
model-based reinforcement learning with latent state
- 运行 base policy \(\pi_{0}(\mathbf{a}_{t}|\mathbf{o}_{t})\), 收集 \(\mathcal{D}=\left\{ (\mathbf{o},\mathbf{a},\mathbf{o}')_{i} \right\}\),
- 学习 \(p_{\phi}(\mathbf{s}_{t+1}|\mathbf{s}_{t},\mathbf{a}_{t})\),\(p_{\phi}(\mathbf{o}_{t}|\mathbf{s}_{t})\),\(p_{\phi}(r_t|\mathbf{s}_{t})\),\(g_{\psi}(\mathbf{o}_{t})\)
- 依据上述模型来进行规划
- 执行第一个规划的 action, 观测到新的状态 \(\mathbf{o}'\) (MPC)
- 添加 \((\mathbf{o},\mathbf{a},\mathbf{o}')\) 到 \(\mathcal{D}\), 重复 3-5; 每 N 次回到 2.
如果我们完全摒弃,回到基于模型的强化学习中的原始方法,但在观察空间直接学习呢?也就是直接学习:
如果面临部分可观测性,那么我们可能需要使用循环模型,让 \(\mathbf{o}_{t+{1}}\) 依赖于旧的状态,从而更好地建模