Offline Reinforcement Learning

约 3788 个字 3 张图片 预计阅读时间 25 分钟

笔记参考： CS285 深度强化学习 (13): Offline Reinforcement Learning (1) - 知乎

slide

Introduction to Offline RL

目前接触到的强化学习算法处理的是一个封闭、规则已知且易于理解的环境，或者这些系统处理的是世界被某种特定环境所包含的设置，但是与监督学习相比，算法难以实现一个很好的泛化性，agent 需要在一个动态变化的环境中做出一系列的决策。

从比较高的层面来看，现代机器学习起效的一个原因是大型数据集和大型高容量模型的组合来得到一个有效的泛化。强化学习中所需要的数据都要通过 agent 与环境的交互生成，数据的分布和质量取决于收集数据时所用的测率，我们没有办法从零构造一个像 ImageNet 这样大的数据集。

无论是 on-policy 还是 off-policy ，它们都是迭代地与环境交互，收集数据，改进策略然后继续收集数据。Offline RL 算法中没有这种主动交互，而是利用了一个缓冲器，我们利用一个策略 \(\pi_{\beta}\) 来收集数据，然后利用这个数据集上来训练我们的策略 \(\pi\)

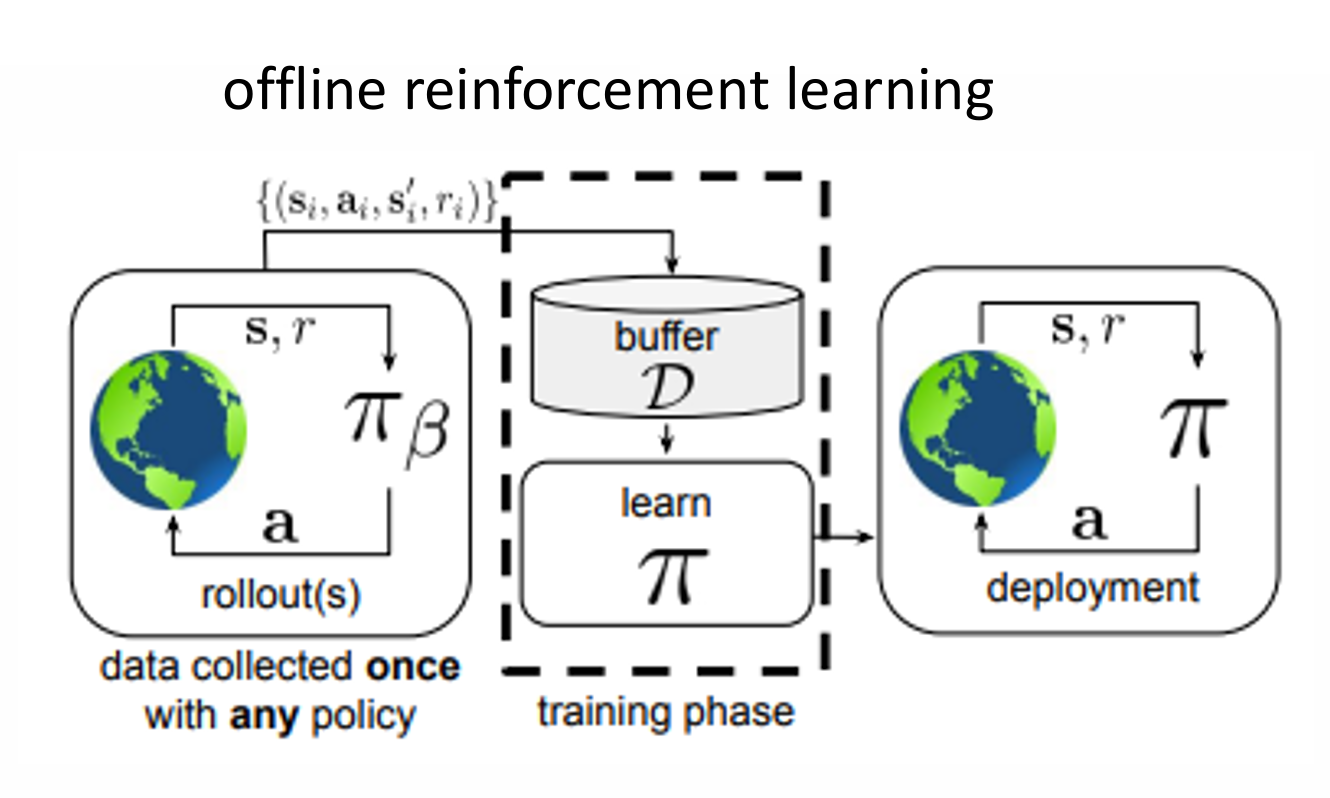
• 数据集 \(\mathcal{D} = \left\{\mathbf{s}_{i} ,\mathbf{a}_{i},\mathbf{s}_{i}',r_{i} \right\}\)
• 状态 \(\mathbf{s}\sim d^{\pi_{\beta}(\mathbf{s})}\)
• 动作 \(\mathbf{a}\sim \pi_{\beta}(\mathbf{a|s})\)，\(\beta\) 表示我们并不知道的策略。
• 下一个状态 \(\mathbf{s}'\sim p(\mathbf{s}'|\mathbf{s},\mathbf{a})\)
• 奖励 \(r \sim r(\mathbf{s},\mathbf{a})\)

我们的目标与之前一样时最大化预期折扣奖励的总和：

\[ \max_{\pi}\sum_{t=0}^{T}\mathbb{E}_{\mathbf{s}_{t}\sim d^{\pi}(\mathbf{s}),\mathbf{a}_{t}\sim \pi(\mathbf{a}|\mathbf{s})} [\gamma^{t}r(\mathbf{s}_{t},\mathbf{a}_{t})] \]

将 offline RL 与 off-policy evalution 进行比较，OPE 的目标是利用固定数据集 \(\mathcal{D}\) 评估当前的 policy ：

\[ J(\pi) = \mathbb{E}_{\pi}\left[ \sum_{t=1}^{T}r(\mathbf{s}_{t},\mathbf{a}_{t}) \right] \]

offline RL （有时候也被称为 batch RL，full off-poliyc RL）的目标则是给定 \(\mathcal{D}\) ，学习最优的策略 \(\pi_{\theta}\) （这里的最优是指数据集上最优，而非整个马尔可夫决策过程）

所以为什么我们仅凭数据集而不与世界互动就能得到好的策略呢？首先，对于 offline RL 算法，我们期望其能够实现几个目标：

• Get order from chaos ：在混杂着好行为与差行为的数据集 \(\mathcal{D}\) 中挑选出好的部分
• Generalization : 某个好的行为在其他状态也能被执行
• Stitching : 将不同行为中好的部分拼接重组

offline RL 与模仿学习不同：offline RL 从理论上可以比数据集中的最好的策略更好，而模仿学习只能得到数据集中的平均策略，我们从大量的次优数据中选取最佳部分并重新拼接起来，这样可以得到一个高度优化的行为。

如果我们能让 offlien RL 算法生效，那么我们就不必在每次训练一个策略时收集一个大规模的数据集，也能将 RL 应用于其他非传统的强化学习问题上，并实现一定程度上的泛化。

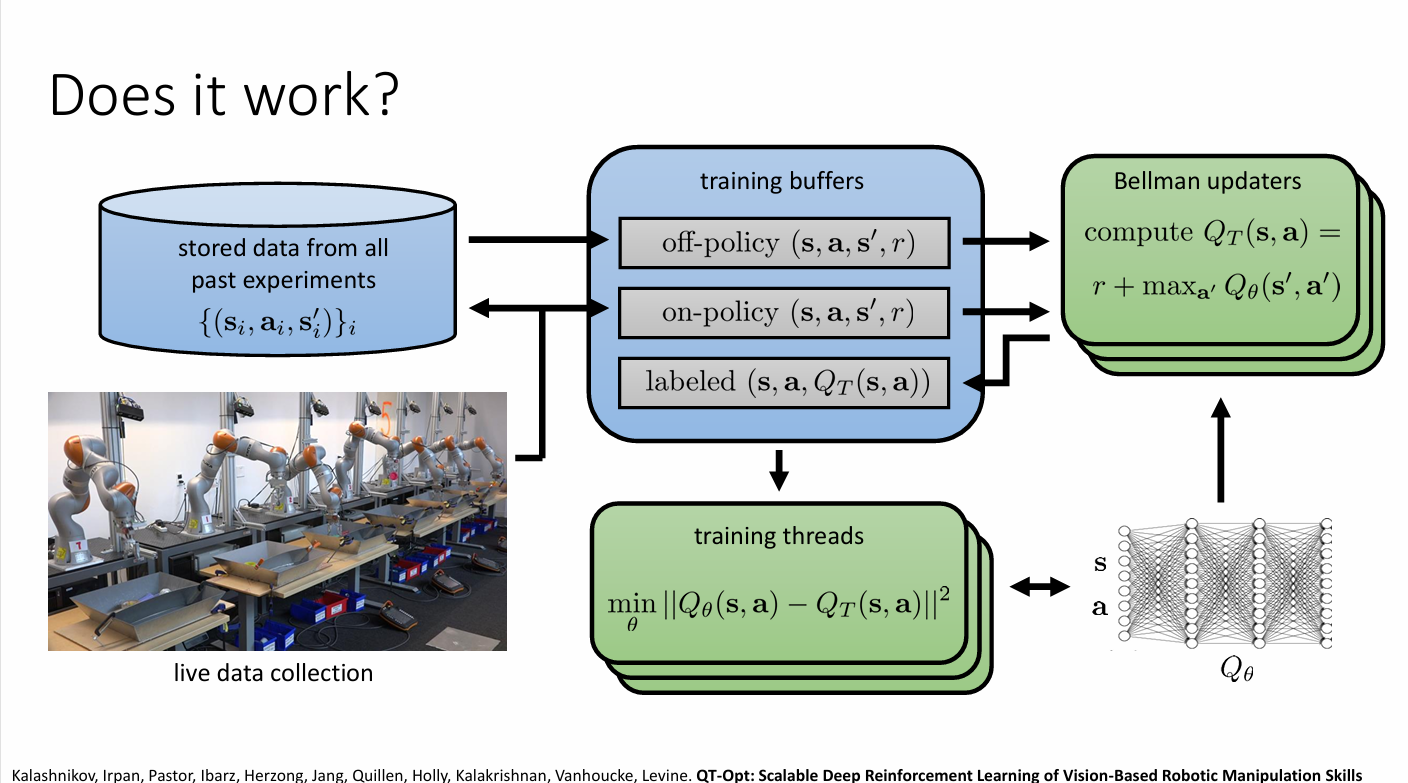
Method	Dataset	Success	Failure
Offline QT-Opt	580k offline	87%	13%
Finetuned QT-Opt	580k offline + 28k online	96%	4%

但 offline RL 算法存在着一些问题，如上表格所示，当我们用一个 580k 离线数据训练模型后再利用 28k 在线数据微调。只用离线数据训练出来的模型成功率达到 87%，而微调出来的模型成功率上升到 4%。于是我们仅省略了 28k 的在线数据，模型的性能下降了很多，也就是说 offline RL 中存在了一些问题限制其表现。另一个问题是，当我们利用一个SAC(软演员-批评家算法)将模型训练到中等奖励（几千左右）然后将缓冲区的数据用于训练 offline RL 算法时，对于不同规模的数据，实际的表现几乎没有区别，如果我们观察 Q-values 曲线会发现估计的 Q-values 非常大。

实际上，这些问题都可以归结于一个基本问题：反事实查询 (counterfactual queries) 。

一个例子是，当我们用驾驶员的数据集来训练模型时，即使驾驶员水平很差，他也不会做一些很疯狂的事情：比如说他也许会闯红灯，但是他不会在马路中间突然拐弯。但是在训练中，对于这些没有见过的事情，比如说马路中间拐弯，模型会思考这个动作会不会带来更高的价值。这些没有见过的状态称为分布外数据（Out of Distribution）对于在线学习方法，我们可以采取简单尝试，发现其带来负收益，然后舍弃这个动作，但是在 offline RL 算法中，我们没有办法处理这些行为，这影响了我们的泛化能力。

在统计学上来说，这是一个分布偏移的问题（Distribution shift）。

在监督学习中，我们通常解决的是一个 empirical risk minimization 问题：

\[ \theta \leftarrow \arg \min_{\theta}\mathbb{E}_{x\sim p(x)y\sim p(y|x)}[(f_{\theta}(x)-y)^{2}] \]

如果没有过拟合问题，那么我们的期望在统计意义上

\[ \mathbb{E}_{x\sim p(x),y \sim p(y|x)}[(f_{\theta}(x)-y)^{2}] \]

会很低，但是对于另一个分布 \(\bar{p}(x)\) ，期望会很高，甚至对于 \(p(x)\) 中的一些点来说，误差也可能很高。

如果我们刻意选择一个 \(x^{*} \leftarrow \arg \max_{x}f_{\theta}(x)\) ，那么我们可能会得到极大的误差\((f_{\theta}(x^{*})-y)\) ，同样的我们可以构造出类似的 \(\bar{p}(x)\) ，使得在这个分布上的误差都很大。

在 \(Q\) 学习中，我们进行如下的更新：

\[ Q(\mathbf{s},\mathbf{a})\leftarrow r(\mathbf{s},\mathbf{a}) + \mathbb{E}_{\mathbf{a}'\sim \pi_{\mathrm{new}}} [Q(\mathbf{s}',\mathbf{a}')] \]

右端就是 \(y(\mathbf{s},\mathbf{a})\) 所以我们的目标函数是

\[ \min_{Q}\mathbb{E}_{(\mathbf{s},\mathbf{a})\sim \pi_{\beta}(\mathbf{s},\mathbf{a})} [(Q(\mathbf{s},\mathbf{a})-y(\mathbf{s},\mathbf{a}))] \]

这就是在 offline RL 下最小化 \(Q\) 和 \(y\) 之间的差异。我们期望 \(\pi_{\beta} = \pi_{\mathrm{new}}\) ，这样我们就可以得到一个比较高的准确性，但是这种事情并不会发生，所以会产生一定的误差。如果我们采用贪婪算法 \(\pi_{new} = \arg \max_{\pi}\mathbb{E}_{\mathbf{a}\sim \pi(\mathbf{a}|\mathbf{s})}[Q(\mathbf{s},\mathbf{a})]\) 事情会变得更糟糕。

在 online RL 算法中，我们可以利用执行策略后收集数据纠正各种泛化，但在 offline 问题中这个问题并没有办法得到纠正，这也意味着采样误差和函数近似误差在 offline RL 算法中愈演愈烈。

Batch RL via Importance Sampling

回顾重要性采样：

\[ \nabla_{\theta}J(\theta) \approx \frac{1}{ N} \sum_{ i =1}^{N} \frac{\pi_{\theta}(\tau_{i})}{\pi_{\beta}(\tau_{i})} \sum_{t=0}^{T} \nabla_{\theta}\gamma^{t} \log \pi_{\theta}(\mathbf{a}_{t,i}|\mathbf{s}_{t,i})\hat{Q}(\mathbf{s}_{t,i},\mathbf{a}_{t,i}) \]

其中重要性比表示为

\[ \frac{\pi_{\theta}(\tau_{i})}{\pi_{\beta}(\tau_{i})} = \prod^{T}_{t=1} \frac{\pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})}{\pi_{\beta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})} \]

这个式子是无偏，但是他随 \(T\) 呈指数级增长，也就意味着需要大量的样本来能实现一个比较精确的估计，同时，随着 \(T\) 的增大，一两个轨迹的权重会因连乘而逐渐变大，导致其他权重与之相比趋近于零，此时相当于用一个极其随意的样本估计原本的策略。因此我们需要舍弃理论上的无偏性，从而换取更低的方差。

在 advanced gradient descent 方法中，一个使用重要性采样的简单方法是舍弃权重中所有时间步长 \(T\) 之前的 \(\pi(\mathbf{a}|\mathbf{s})\) ，如果 \(\pi_{\theta}\) 与 \(\pi_{\beta}\) （生成数据的策略）相似，那么这样的做法是合理的，但这个思想不适用于 offline RL ，因为在 offline RL 中，我们是希望得到一个更好的策略，而不是相似的。

分解原来的重要性采样的式子：

\[ \nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \left( \prod_{t' =0}^{t-1}\frac{\pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})}{\pi_{\beta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})}\right)\nabla_{\theta} \gamma^{t}\log \pi_{\theta}(\mathbf{a}_{t,i}|\mathbf{s}_{t,i})\left( \prod^{T}_{t'= t}\frac{\pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})}{\pi_{\beta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})} \right)\hat{Q}(\mathbf{s}_{t,i},\mathbf{a}_{t,i}) \]

第一部分的重要性比考虑了到达 \(\mathbf{s}_{i,t}\) 状态的概率差异，第二部分的重要性比考虑了 \(Q\) 值的差异。对于在线学习方法，如果 \(\pi_{\theta}\) 和 \(\pi_{\beta}\) 的分布差异不大的话是可以省略的，或者说我们不再考虑最大化 \(\pi_{\theta}\) 在其自身状态分布下的期望回报，而是退而求其次最大化 \(\pi_{\theta}\) 在行为策略 \(\pi_{\beta}\) 的状态分布下的期望回报。

现在考虑第二部分，做如下简化：

\[ \left( \prod^{T}_{t'= t}\frac{\pi_{\theta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})}{\pi_{\beta}(\mathbf{a}_{i,t}|\mathbf{s}_{i,t})} \right)\hat{Q}(\mathbf{s}_{t,i},\mathbf{a}_{t,i}) =\sum_{t'=t}^{T} \left( \prod_{t'' = t}^{t'}\frac{\pi_{\theta}(\mathbf{a}_{i,t''}|\mathbf{s}_{i,t''})}{\pi_{\beta}(\mathbf{a}_{i,t''}|\mathbf{s}_{i,t''})} \right)\gamma^{t'-t} r_{i,t'} \]

这个简化式子依旧是一个指数变化的，但是稍微改进了以下方差。实际上很多优化技巧都很难改变指数变化这件事，但从不同程度上都降低了方差。但是，为了避免 exponentially exploding importance weights 的问题，需要使用 value function estimation 技术。

\[ \begin{align} V^{\pi_{\theta}}(\mathbf{s}_{0}) &\approx \sum_{t=0}^{T} \left( \prod_{t' =0}^{t} \frac{\pi_{\theta}(\mathbf{a}_{t'}|\mathbf{s}_{t'})}{\pi_{\beta}(\mathbf{a}_{t'}|\mathbf{s}_{t'})} \right) \\ & = \sum_{t=0}^{T}\left( \prod^{t}_{t' =0}\rho_{t'} \right)\gamma^{t }r_{t} \\ &=\rho(r_{0} + \gamma(\rho_{1}(r_{1}+\gamma(\rho_{2}(r_{2})+\gamma\dots)))) \end{align} \]

对于上式，我们只是做了简单的乘法展开和结合律的使用，将上式记作 \(\bar{V}^{T}\) 可以得到一个递推式

\[ \bar{V}^{T+1-t} = \rho_{t}(r_{t}+\gamma \bar{V}^{T-t}) \]

在单臂老虎机问题中，可以做如下近似：

\[ V_{DR }(s) = \hat{V}(s) + \rho(s,a)(r_{s,a}-\hat{Q}(s,a)) \]

其中 \(\hat{V}(\mathbf{s})\) 和 \(\hat{Q}(\mathbf{s},\mathbf{a})\) 都是函数估计器，这种近似方法称为 doubly robust estimation 。简单来说就是我们有两个模型，我们用第一个模型做了一个初步的预测，然后用另一个模型计算真实结果和模型预测之间的残差，对这个残差进行加权，最后得到真实的估计值，只要这两个模型中有任意一个模型是正确的，最终估计结果就是无偏的，因此给了更多的容错空间。不过这是一个 Off-Policy Evaluation ，并不是一个 RL 算法。

这个方法和上面的递推式结合起来可以得到：

\[ V_{DR }^{T+1-t}= \hat{V}(\mathbf{s}_{t}) + \rho_{t}(r_t+\gamma \bar{V}^{T-t}_{DR}-\hat{Q}(\mathbf{s}_{t},\mathbf{a}_{t})) \]

之前的重要性采样都是基于轨迹的，而现在我们尝试对状态-动作的边际分布做重要型采样：

\[ w(\mathbf{s},\mathbf{a}) = \frac{d^{\pi_{\theta}}(\mathbf{s},\mathbf{a})}{d^{\pi_{\beta}}(\mathbf{s},\mathbf{a})} \]

显然我们并不知道这个值，但是假如我们知道就能用如下方法计算目标函数：

\[ J(\theta) \approx \frac{1}{N} \sum_{i}w(\mathbf{s}_{i},\mathbf{a}_{i})r_{i} \]

这种方法常用于 off-policy evaluation 。

Batch RL via Linear Fitted Value Functions

Note

这边可以看笔记参考，写的比较随意

另一种用于 Batch RL 的学习方法是采用线性拟合值函数，不过现在更多采用深度神经网络来拟合函数。

一般而言，人们会将 offline 值函数估计问题视作是将现有的近似动态规划和 \(Q\) 学习思想扩展到离线环境中，并利用线性函数近似俩获取封闭解。而现在，我们倾向采用深度神经网络作为我们的模型，这个方法面临的问题正是之前所讨论的分布偏移，但对于传统线性值函数拟合，因为模型比较简单所以可以不处理分布偏移的问题。

我们希望得到一个形如 \(Aw = b\) 的方法来估计价值函数，先考虑一个 \(\lvert S \rvert\times K\) 的特征空间 \(\Phi\) ，其中每一行表示一个状态的特征，利用最小二乘法推导得到表达式。

• 估计奖励权重 ：\(\Phi w_{r} \approx \vec{r}\)

\[ w_{r} = (\Phi^{T}\Phi)^{-1}\Phi^{T}\vec{r} \]

• 估计转移矩阵 ：\(\Phi P^{\pi}_{\Phi} = P^{\pi}\Phi\)

\[ P^{\pi}_{\phi} = (\Phi^{T} \Phi)^{-1}\Phi^{T}P^{\pi}\Phi \]

• 估计价值函数权重：\(V^{\pi}=\Phi w_{V}\)

\[ w_{V} = (\Phi^{T}\Phi-\gamma \Phi^{T}P^{\pi}\Phi)^{-1}\Phi^{T}\vec{r} \]

我们通过特征变换得到了 \(w_{r}\) ，进而得到价值函数，进而利用价值函数来改进的策略。除了特征变换外，我们还需要利用样本来估计 \(\vec{r}\) 和 \(P^{\pi}\) ，这个做法称为 least-squares temporal difference 。我们更希望得到一个无模型的算法.

考虑 \(\mathcal{D} = \left\{ (\mathbf{s}_{i},\mathbf{a}_{i},r_{i},\mathbf{s}_{i}') \right\}\) ，由于我们并没有全体状态，所以可以考虑用一个 \(\lvert \mathcal{D} \rvert\times K\) 的矩阵 \(\Phi'\) 来表示经验上的特征空间，其中的每一行表示一个样本的特征 \(\phi(\mathbf{s}_{i}')\) ，类似地可以用 \(\vec{r}_{i} = r(\mathbf{s}_{i})\) 来估计 \(\vec{r}\)。整个算法就是：

1. \(\pi'(\mathbf{s})\leftarrow \mathrm{Greedy}(\Phi w_{V})\)
2. 估计 \(V^{\pi'}\)

整个算法和价值迭代是非常相似的，但是主要的区别是使用了特征变换而不是在状态空间中进行操作。

但是前面用样本估计时，我们要求样本来源于 \(\pi\) ，但是在offline RL 算法中，我们没有相应的样本。而且如果我们只有V函数，要进行策略改进（即选出最优动作），我们需要知道状态转移模型：\(\pi'(\mathbf{s}) = \arg\max_{\mathbf{a}} \sum_{\mathbf{s}'} P(\mathbf{s}'|\mathbf{s},\mathbf{a})[r(\mathbf{s},\mathbf{a},\mathbf{s}') + \gamma V(\mathbf{s}')]\)。一个解决方法是用 \(Q\) 函数来替代 \(V\) 函数，此时 \(\Phi\) 是一个 \(\lvert \mathcal{S} \rvert\lvert A \rvert\times K\) 的矩阵，其中每一行表示一个状态动作对的特征。

我们同样可以推导出

\[ w_{Q} = (\Phi^{T}\Phi-\gamma \Phi^{T}P^{\pi}\Phi)^{-1}\Phi^{T}r \]

最终得到了 LSPI 算法

1. 计算 \(\pi_{k}\) 对应的 \(w_{Q}\)
2. 更新 \(\pi_{k+1}(\mathbf{s} = \arg \max_{\mathbf{a}}\phi(\mathbf{s},\mathbf{a}))w_{Q}\)
3. 令 \(\Phi'_{i} = \phi(\mathbf{s}_{i}',\pi_{k+1}(\mathbf{s_{i}'}))\)

但是算法并没有解决分布偏移问题。