Introduction To Reinforcement Learning

约 2861 个字 3 张图片 预计阅读时间 19 分钟

Sildes

Markov chain

奖励函数(reward function) \(r(s,a)\) 是状态（state）和动作（action）的一个衡量函数，他告诉我们哪个状态和动作更好。\(s,a,r(s,a),p(s'|s,a)\) 定义了 Markov 决策过程

Markov chain - Wikipedia

Markov chain：

\[ \mathcal{M}=\left\{ \mathcal{S,T} \right\} \]

• \(\mathcal{S}\) 状态空间(state space)
• \(\mathcal{T}\) 转移算子(transition operator) \(p(s_{t+{1}}|s_{t})\)

考虑 \(\mu_{t,i}=p(s_{t}=i)\) 表示 \(t\) 时刻第 \(i\) 种状态的可能，\(\vec{\mu}_{t}\) 则 \(t\) 时刻可能状态概率的向量，取 \(\mathcal{T}_{i,j}=p(s_{t+1}=i|s_{t}=j)\) 则 \(\vec{\mu}_{t+1}= \mathcal{T}\vec{\mu}_{t}\) 这就是为什么被叫做算子(operator)

Markov 特性：与 \(s_{t-1}\) 状态独立，也就是在给定状态时，他与过去状态时条件独立

Markov decision process - Wikipedia

Markov decision Process

\[ \mathcal{M=\left\{ S,A,T,r \right\} } \]

• \(\mathcal{A}\) 动作空间(action space)
• \(r\) 奖励函数(reward function) \(r :\mathcal{S\times A}\to \mathbb{R}\)

取 \(\mu_{t,j}=p(s_{t}=j),\xi_{t,k}=p(a_{t}=k),\mathcal{T}_{i,j,k}=p(s_{t+1}=i|s_{t}=j,a_{t} =k)\) ，则

\[ \mu_{t+1,i}=\sum_{j,k}^{} \mathcal{T}_{i,j,k}\mu_{t,j}\xi_{t,k} \]

马尔可夫决策过程是马尔可夫链的推广，不同之处在于添加了行动（允许选择）和奖励（给予动机）。反过来说，如果每个状态只存在一个操作和所有的奖励都是一样的，一个马尔可夫决策过程可以归结为一个马尔可夫链。

Partially observable Markov decision process - Wikipedia

Partially Observable Markov Decision process

\[ \mathcal{M=\left\{ S,A,O,T,E,r \right\} } \]

• \(\mathcal{O}\) 观察空间(observation space)
• \(\mathcal{E}\) 发射概率(emisssion probability)

\(\pi_{\theta}\) 是我们训练出来的策略，\(\theta\) 指的是策略的相关参数，比如说我们所采取的策略是一个深度学习的网络，则 \(\theta\) 为网络的层数。强化学习的目标不仅仅是采取当前高奖励的动作，而是采取能够带来未来更高奖励的动作。

轨迹分布：

\[ \underbrace{ p_\theta(s_{1},a_{1},\dots,s_{T},a_{T}) }_{p_{\theta}(\tau)}= p(s_{1})\prod_{t=1}^{T}\underbrace{\pi_{\theta}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t}) }_{\text{Markov chain on}(\mathbf{s,\mathbf{a}})} \]

强化学习的目标是

\[ \theta ^{*} =\underset{ \theta }{ \arg \max }\mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t }^{} r(s_{t},a_{t}) \right] \]

我们希望的一个策略，使得我们的轨迹分布的期望得到尽可能高的奖励，这个期望值考虑了策略的随机性、转移概率以及初始状态分布

\[ p((s_{t+1},a_{t+1})|(s_{t},a_{t}))=p(s_{t+1}|s_{t},a_{t}) \pi_{\theta}(a_{t+1}|s_{t+1}) \]

由于期望具有线性性，我们可以交换求和和期望

\[ \begin{align} \theta ^{*} &=\underset{ \theta }{ \arg \max }\mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t }^{} r(s_{t},a_{t}) \right] \\ &=\underset{ \theta }{ \arg\max }\sum_{t=1}^{T}\mathbb{E}_{(s_{t},a_{t})\sim p_{\theta(s_{t},a_{t})}} [r(s_{t},a_{t})] \end{align} \]

这意味着我们可以单独考虑每个时间步的奖励的期望，而不一次性考虑整个轨迹。

上面讨论的都是 Finite Horizon 的问题，这也就是时域有限。当 \(T = \infty\) ，也就是 infinite horizon 问题时，假如我们的奖励是正的，那么无限个正数的和会趋向正无穷。一种处理方法是采用平均期望求和（这不是最常用的），也就是将我们得到的期望除以 \(T\) ，如果时间和期望趋于无穷的话，平均期望理论上能够趋向一个特定的值。

\[ \frac{1}{T}\mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t =1}^{T} r(s_{t},a_{t}) \right] \]

我们希望 \(p(s_{t},a_{t})\) 随着时间的增加趋向于一个平稳分布(stationary distribution)（在遍历性和链的无周期性的情况下，我们可以实现这件事情，遍历性是指无论从那种状态开始，经过一定步数后有可能达到任何其他状态的性质）。

\[ \mu = \symcal{T} \mu \]

也就是说转移前后状态相同，那么

\[ \begin{pmatrix} s_{t+1} \\ a_{t+1} \end{pmatrix} =\mathcal{T} \begin{pmatrix} s_{t} \\ a_{t} \end{pmatrix}\quad\begin{pmatrix} s_{t+k} \\ a_{t+k} \end{pmatrix} =\mathcal{T}^{k} \begin{pmatrix} s_{t} \\ a_{t} \end{pmatrix} \]

实际上 \(\mu\) 是如下特征方程的解

\[ (\mathcal{T}-I)\mu =0 \]

其实也就是转移矩阵 \(\mathcal{T}\) 特征值为 \(1\) 时所对应的特征向量

在强化学习，我们所关心的是期望。考虑一个例子，当自动驾驶车在岸边时，冲下岸的奖励为 \(-1\) ，没有冲下岸的奖励为 \(1\) ，取 \(\pi_{\theta} (a = \text{fall}) =\theta\) ，显然奖励函数是一个离散分布，我们很难用凸方法来优化他们（因为不是光滑的），但是奖励函数的期望 \(\mathbb{E}_{\pi}[r(x)]\) 一般是关于 \(\theta\) 的光滑函数。

Value Functions

轨迹函数

\[ \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t=1}^{T} r(s_{t},a_{t}) \right] \]

用链式法则展开

\[ \mathbb{E}_{s_{1}\sim p_{s_{1}}}\left[ \mathbb{E}_{a_{1}\sim \pi(a_{1}|s_{1})}[r(s_{1},a_{1})+\mathbb{E}_{s_{2}\sim p(s_{2}|s_{1},a_{1})}[ \mathbb{E}_{a_{2}\sim \pi(a_{2}|s_{2})}[r(s_{2},a_{2})+\dots|s_{2}]|s_{1},a_{1}]|s_{1} ] \right] \]

取

\[ Q(s_{1},a_{1}) = r(s_{1},a_{1})+\mathbb{E}_{s_{2}\sim p(s_{2}|s_{1},a_{1})}[ \mathbb{E}_{a_{2}\sim \pi(a_{2}|s_{2})}[r(s_{2},a_{2})+\dots|s_{2}]|s_{1},a_{1}] \]

则期望可以简写成

\[ \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t=1}^{T} r(s_{t},a_{t}) \right]=\mathbb{E}_{s_{1}\sim p_{s_{1}}}\left[ \mathbb{E}_{a_{1}\sim \pi(a_{1}|s_{1})}[Q(s_{1},a_{1})|s_{1}] \right] \]

如果我们知道 \(Q(s_{1},a_{1})\) ，我们能够比较容易定义 \(\pi_{\theta}(a_{1}|s_{1})\)。一个简单的例子时，当 \(a_{1} = \underset{ a_{1} }{ \arg\max }Q(s_{1},a_{1})\) 也就是选择使得 \(Q\) 函数最大化的动作，或者说是一个确定性的最优动作，那我们的策略 \(\pi(a_{1}|s_{1})=1\) ，也就是我们总是选择这个动作

Q 函数：在状态 \(s_{t}\) 下采取 \(a_{t}\) 动作的所有奖励

\[ Q^{\pi}(s_{t},a_{t})=\sum_{t'=t}^{T}\mathbb{E}_{\pi_{\theta}}[r(s_{t'},a_{t'})|s_{t},a_{t}] \]

上面我们已经定义好了Q函数，需要注意的是Q函数是和一个策略绑定在一起的，这个策略就是 \(\pi\), 从Q函数的定义也知道Q函数就是对于在状态 \(s_{t}\) 的时候选择 动作 \(a_{t}\) 所获得的未来奖励期望的总和，而要知道未来奖励就需要有一个策略来从当前的状态 \((s_{t},a_{t})\) 出发一直运行到最后即可得到总的未来奖励即可

值函数(Value function)：状态 \(s_{t}\) 的所有奖励

\[ V^{\pi}(s_{t})=\sum_{t'=t}^{T}\mathbb{E}_{\pi_{\theta}}[r(s_{t'},a_{t'})|s_{t}] \]

\[ V^{\pi}(s_{t})=\mathbb{E}_{a_{t}\sim \pi(a_{t}|s_{t})}[Q^{\pi}(s_{t},a_{t})] \]

值函数也是和策略绑定在一起的，但其余 Q 函数只差了 \(a_{t}\) 一项。具体来说，在 Q 函数中 \(a_{t}\) 是一个常数已经给定的值，而 \(a_{t+1},\dots,a_{T}\) 这些动作是通过策略 \(\pi\) 选择出来的，但是在值函数中，\(a_{t}\) 也是由策略 \(\pi\) 选择出来的。

为什么要定义Q函数和值函数呢？有两个直观的动机，在后边的算法中会反复用到这两个动机，在这里我们只是初步展示一下这个思路，并不是很严谨，大家在这里只需要建立一些基本的概念即可。

• Idea 1：当通过 \(\pi\) 生成 Q 函数之后，我们可以通过选择最大的 \(Q(s,a)\) 得到一个新的策略，而且我们知道这个新的策略不会比之前的策略 \(\pi\) 差，这个性质称为策略改进(policy Improvement) 。
• Idea 2：可以通过求 \(Q(s,a)\) 的梯度增加生成一个好的动作的可能。

Algorithms

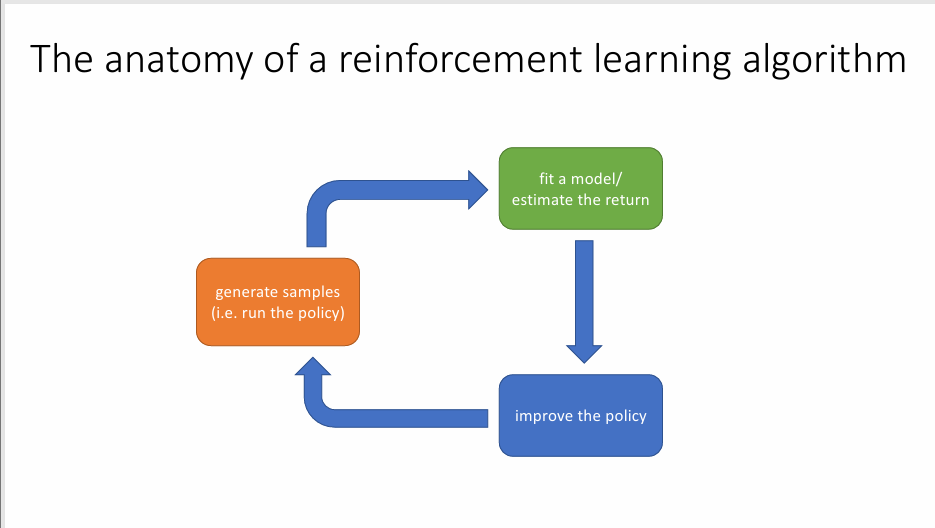
强化学习算法一般由下面三部分组成

• 生成样本，在你的环境中运行你的策略，让它和马尔可夫决策过程进行交互并收集样本，样本也就是轨迹。
• 训练模型，选定一种方法来估计当前策略的好坏
• 改进策略，根据估计结果来优化我们的算法

简而言之就是：运行策略，获取一些轨迹，衡量这些轨迹的好坏， 然后修改策略以使更好的轨迹又更高的概率出现

一个简单的例子：训练模型（奖励的均值）

\[ J(\theta) = E_{\pi}\left[ \sum_{t}^{} r_{t} \right] \approx \frac{1}{N}\sum_{i=1}^{N}\sum_{t}^{}r^{i}_{t} \]

改进策略（梯度下降）

\[ \theta \leftarrow \theta +\alpha \nabla_{\theta}J(\theta) \]

或者可以设计一个神经网络作为你的模型

\[ s_{t+1} \approx f_{\phi }(s_{t},a_{t}) \]

我们用反向传播来改进策略

考虑这三个部分的成本，这关系到我们如何选定合适的算法： - 生成样本：时间和计算成本取决于你解决的问题，真实问题代价比较高，模拟问题代价比较低 - 训练模型：取决于你的模型，取均值的方法比较简单，神经网络方法成本比较高 - 改进策略：取决于你的优化方法，梯度下降成本低，回溯算法成本高

强化学习的目标：

\[ \theta ^{*} =\underset{ \theta }{ \arg \max }\mathbb{E}_{\tau\sim p_{\theta}(\tau)} \left[ \sum_{t }^{} r(s_{t},a_{t}) \right] \]

集中常见的算法：

• 策略梯度法(Policy gradients)：计算该目标关于 \(\theta\) 的导数，利用导数进行梯度下降
• 基于价值(Value-based)：估计最优策略的价值函数或者 Q 函数，利用用这些来改进策略，但并不直接表示策略而是简洁表示
• 表演-批评者(Actor-critic)：学习 \(Q\) 函数，用这些函数来改进策略，通过他们来计算更优的梯度
• 基于模型(Model-based RL)：估计一个转移模型 ，用这些转移模型进行规划，但不涉及任何显式策略，或者用这些模型来改进策略

基于模型的强化学习

• 训练模型 ：学习 \(p(s_{t+1}|s_{t},a_{t})\)
• 改进策略：
  • 直接规划
  • 计算奖励函数关于策略的导数（利用反向传播）
  • 学习一个价值函数，用这些函数来改进策略（无模型学习）

基于价值函数的强化学习

• 训练模型： \(V(s)\) 或者 \(Q(s,a)\)
• 改进策略：设定 \(\pi(s)=\arg \max Q(s,a)\)

基于梯度算法的强化学习

• 训练模型：评估 \(R_{\tau}=\sum_{t}^{}r(s_{t},a_{t})\)
• 改进策略：\(\theta \leftarrow\theta +\alpha \nabla_{\theta}\mathbb{E}\left[ \sum_{t}^{}r(s_{t},a_{t}) \right]\)

表演者-批评者

• 训练模型：\(V(s)\) 或者 \(Q(s,a)\)
• 改进策略：\(\theta \leftarrow\theta+\alpha \nabla_{\theta}\mathbb{E}[Q(s_{t},a_{t})]\)

衡量模型

• 不同取舍因素
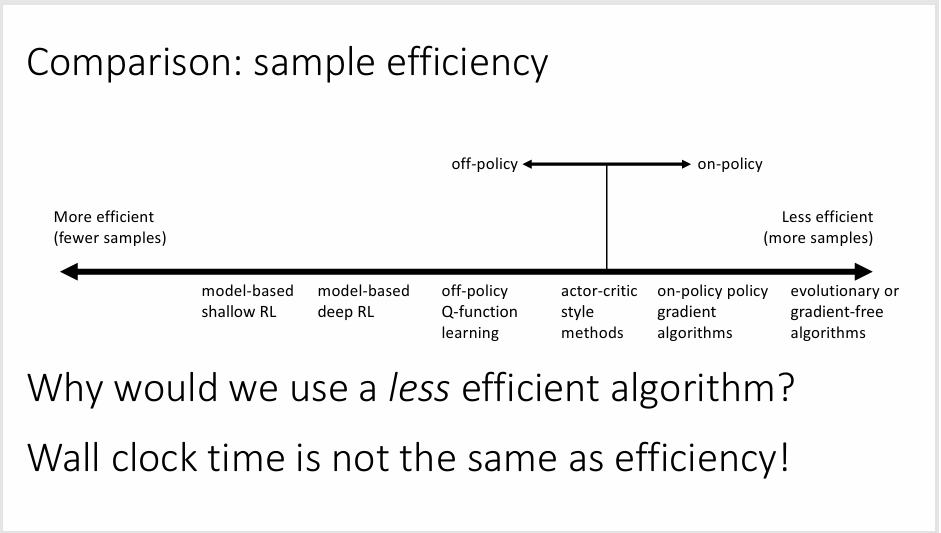
  • 样本效率（需要多少样本才能获得一个更好的策略）
  • 稳定性与易用性（取舍不同参数）
• 不同假定
  • 随机或者确定
  • 连续或者离散
  • 有限时域或无限时域
• 不同情况下的表现
  • 便于展示模型
  • 便于展示策略

样本效率：我们需要从策略采样多少次才能获得一个比较好的表现

• 离策略：不需要新样本就能改进模型
• 同策略：模型的改变需要生成新的样本