自由振动

约 558 个字 2 张图片 预计阅读时间 4 分钟

振动系统介绍

对于以一个实际自由振动系统，可以简化成一个包含恢复力\(k(x)x\)、激励 \(F(t)\)、阻尼力\(c(x,\dot{x})\dot{x}\) 的运动模型。

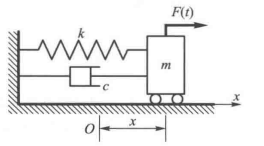
单自由系统的运动方程

\[ m \ddot{x} + c\dot{x}+kx = F(t) \]

恢复力\(k(x)x\)可表示成：

\[ g(x) =k_1x+k_2x^2+k_3x^3+\cdots \]

非线性阻尼 \(c(x,\dot{x})\dot{x}\)

\[ c(x,\dot{x})\dot{x} = (c_0+c_1x^2+c_2\dot{x}^2)\dot{x} \]

含有上述非线性阻力的系统称为VanderPol振子

当只含有线性刚度\(k_1\)和三次刚度\(k_3\)的系统称为Duffing振子。

Duffing和VanderPol的组合称为Duffing -VanderPol oscillator(杜芬范德尔波振子)

我们会在非线性振动中具体讨论。

振动的分类：

• 系统响应：
  1. 定则振动：一个确定性系统在受到确定性激扰时，响应也是确定性的
  2. 随机振动：系统受到随机激扰，响应式随机的
• 激扰控制：
  1. 自由振动；
  2. 强迫振动；
  3. 自激振动；
  4. 参激振动；

激励类型：

• 外加激励:
  1. 直接施加
  2. 基础运动，如相对运动。 当\(F(t)=0,m(\ddot{x}+\ddot{x}_g(t))+c\dot{x} + kx =0\Rightarrow m\ddot{x}+c\dot{x}+kx = -m\ddot{x}_g(t)\)
• 参数激励 \(m\ddot{x}+c_0\dot{x}+k_0x = -g_1(t)x-g_2(t)\dot{x}-g_3(t)\ddot{x}\)

激励\(F(t)\)

• 谐和激励 \(F(t) = \sum^{n}_{i=1}A_i sin(w_i t + \varphi_i)\)
• 周期激励 \(F(t+\tau) = F(t)\)，对激励进行傅里叶展开得：\(F(t) = A_0+\sum^{\infty}_{i=1}A_i \cos(\frac{2\pi i}{T}t+\varphi_i)\)
• 任意激励 满足条件 \(\int^{+\infty}_{-\infty}|F(t)|dt<\infty\) 频谱连续
• 随机激励

随机激励是非定则（他的规律无法用时间的确定函数来描述）的激励，他无法用时间确定函数来描述，但具有一定的统计规律性，可以将随机激励转换成相关函数处理。

自相关函数 \(R_x(\tau)\) ：随机变量\(X(t_1)\)与\(X(t_2)\)乘积的集合平均，描述随机变量的“平均功率”随时差的变化，

\[ R_x(\tau) = E[X(t)X(t+\tau)] = \int^{\infty}_{-\infty}\int^{\infty}_{-\infty}x_1x_2p(x_1,x_2,\tau)dx_1dx_2 \]

功率谱密度 \(S_x\) 描述随机变量的“平均功率”按频率的分布

\[ S_x(f) = \int^{\infty}_{-\infty} R_x(\tau)e^{-2\pi i/\tau}d\tau \]

也可以这样定义：

\[ S_x(f) = \lim_{T\rightarrow \infty}\left\{E\left[\frac{1}{T}|X_T(t)|^2\right]\right\} \]

在随机振动理论中，功率谱法占有极为重要的地位。

关于更多随机激励的问题可见下一章的讨论

---

\[ m \ddot{x} + c\dot{x}+kx = F(t) \]

化作阻尼自由振动的标准形式：

\[ \ddot{x} +2\xi\omega_0\dot{x}+\omega_0^2x = f(t) \]

\(\omega_0= \sqrt{\frac{k}{m}}\)称为固有频率 \(\xi = \frac{c}{2m\omega_0 }\)称为阻尼系数，这是一个无量纲常数 求解特征方程可得

\[ \lambda_{1,2} = -\xi \pm \sqrt{\xi^2-1}w_0 \]

阻尼比	特征值	解
\(\xi<1\)	\(\lambda _{1,2} = -\xi \omega_0 \pm i\sqrt{1-\xi^2}w_0\)	\(e^{-\xi \omega_0 t}(C_1\sin\sqrt{1-\xi^2}\omega_0 t+C_2\cos\sqrt{1-\xi^2}\omega_0 t)\)
\(\xi=1\)	\(\lambda_{1,2}= \omega_0\)	\(C_1 e^{-\omega_0 t}+C_2 te^{-\omega_0t}\)
\(\xi>1\)	\(\lambda _{1,2} = -\xi \omega_0 \pm \sqrt{\xi^2-1}w_0\)	\(e^{-\xi\omega_0}(C_1e^{\sqrt{\xi^2-1}t}+C_2e^{\sqrt{\xi^2+1}t})\)

只有当\(\xi<1\)时称自由振动，一般只考虑这种情况

单位脉冲响应

\[ \begin{cases} \ddot{x} + 2\xi \omega_0\dot{x}+\omega_0^2x= \delta(t)\\ x(0) = \dot{x}(0) = 0 \end{cases} \]

对应解

\[ h(t)= \frac{1}{\sqrt{1-\xi^2}w_0} e^{-\xi\omega_0 t}\sin(\sqrt{1-\xi^2}\omega_0 t) \]

大概运动图像：

• 周期：\(T = \frac{2\pi}{\sqrt{1-\xi^2}\omega_0}\)
• 赋值衰减：\(e^{-\xi \omega_0 T}\)

于是对于任意脉冲函数 \(f(t)\delta(t)\) 我们可以给出解

\[ x(t) = f(t) h(t) \]

如何计算\(\xi\)：

当\(\xi\)较小时，取

\[ T\approx \frac{2\pi}{\omega_0} \]

则取两个赋值，可得衰减值

\[ \frac{A_2}{A_1} = e^{-\xi \omega_0T} \]

取对数后变换得

\[ \xi = \frac{1}{2\pi}\ln\frac{A_1}{A_2} \]

也可以选定特定的幅值来计算