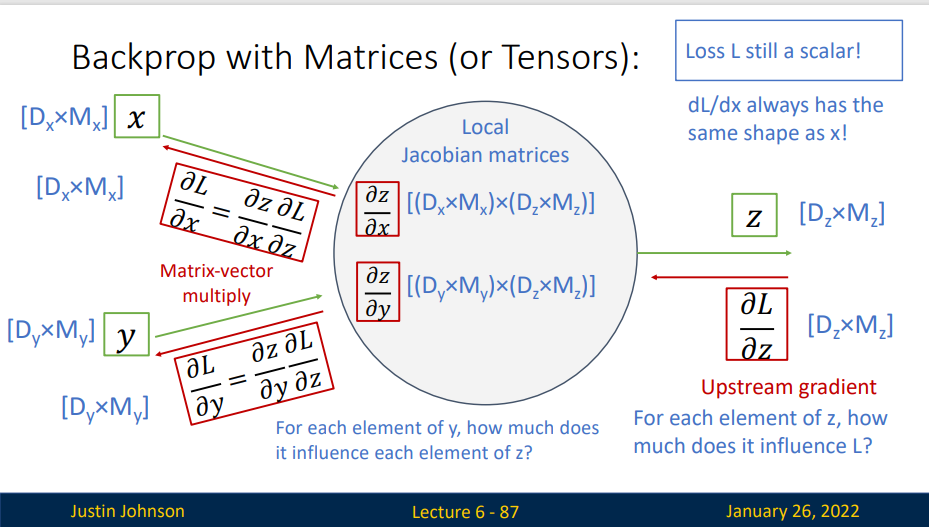
Backpropagation
约 1173 个字 6 张图片 预计阅读时间 8 分钟
Total loss
显然,如果我们想要通过SGD方法来优化损失函数,我们需要计算\(\frac{\partial L}{\partial W_1},\frac{\partial L}{\partial W_2},\frac{\partial L}{\partial b_1},\frac{\partial L}{\partial b_2}\)。
那我们如何计算偏导数呢?在自动微分之前,我们一般直接手算表达式,但是这样简单粗暴的方法带来了一系列问题 1. 这是一件非常的繁琐的事情,需要大量的矩阵计算。 2. 如果我们想要对模型进行微小调整则需要重新计算倒数。 3. 对于一些复杂模型而言,这并不是一件很容易的事。
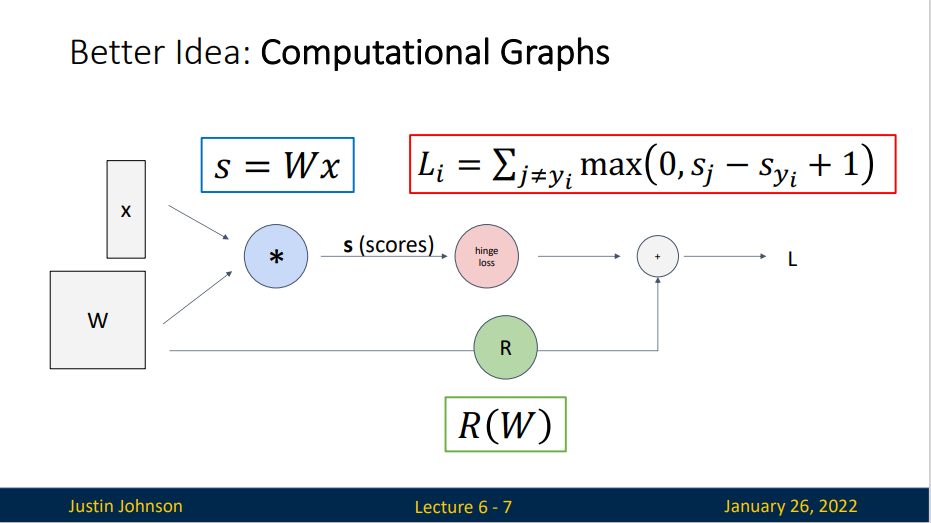 绘制计算图有助于我们可视化计算中操作符和变量的依赖关系。正方形表示变量,圆圈表示操作符。 左下角表示输入,右上角表示输出。 注意显示数据流的箭头方向主要是向右和向上的。
绘制计算图有助于我们可视化计算中操作符和变量的依赖关系。正方形表示变量,圆圈表示操作符。 左下角表示输入,右上角表示输出。 注意显示数据流的箭头方向主要是向右和向上的。
backprogation
反向传播(backward propagation或backpropagation)指的是计算神经网络参数梯度的方法。 简言之,该方法根据微积分中的链式规则,按相反的顺序从输出层到输入层遍历网络。 该算法存储了计算某些参数梯度时所需的任何中间变量(偏导数)。 假设我们有函数\(Y=f(X)\)和\(Z=g(Y)\), 其中输入和输出\(X,Y,Z\)是任意形状的张量。 利用链式法则,我们可以计算Z关于X的导数
在这里,我们使用prod运算符在执行必要的操作(如换位和交换输入位置)后将其参数相乘。 对于向量,这很简单,它只是矩阵-矩阵乘法。 对于高维张量,我们使用适当的对应项。 运算符prod指代了所有的这些符号。
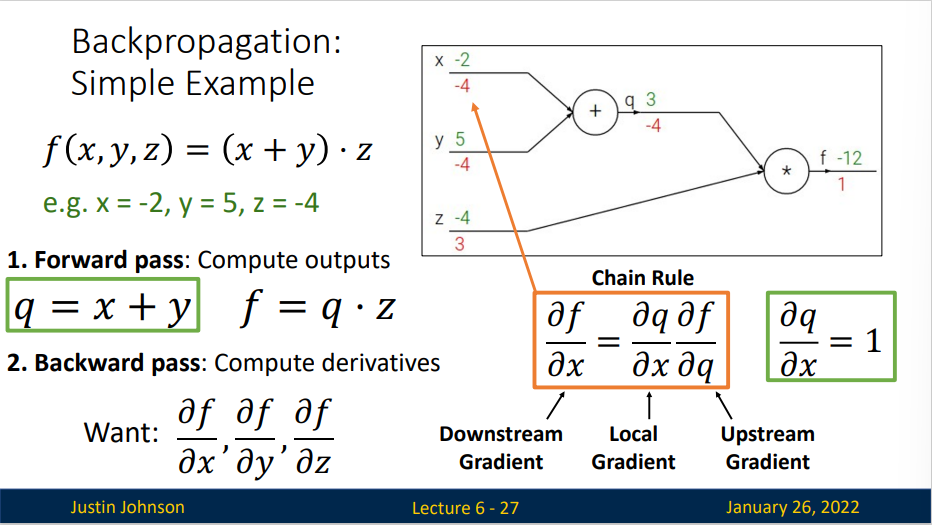 前向传播从输入计算到输出(绿色),反向传播从尾部开始,根据链式法则递归地向前计算梯度(显示为红色),一直到网络的输入端。可以认为,梯度是从计算链路中回流。
前向传播从输入计算到输出(绿色),反向传播从尾部开始,根据链式法则递归地向前计算梯度(显示为红色),一直到网络的输入端。可以认为,梯度是从计算链路中回流。
反向传播是一个优美的局部过程。在整个计算线路图中,每个门单元都会得到一些输入并立即计算两个东西:这个门的输出值,和其输出值关于输入值的局部梯度。门单元完成这两件事是完全独立的,它不需要知道计算线路中的其他细节。然而,一旦前向传播完毕,在反向传播的过程中,门单元门将最终获得整个网络的最终输出值在自己的输出值上的梯度。链式法则指出,门单元应该将回传的梯度乘以它对其的输入的局部梯度,从而得到整个网络的输出对该门单元的每个输入值的梯度。
这里对于每个输入的乘法操作是基于链式法则的。该操作让一个相对独立的门单元变成复杂计算线路中不可或缺的一部分,这个复杂计算线路可以是神经网络等。
我们需要考虑一些事情: 对前向传播变量进行缓存:在计算反向传播时,前向传播过程中得到的一些中间变量非常有用,所以在实际操作过程最好实现对这些中间变量的缓存。 不同分支的梯度相加:如果变量x,y在前向传播的表达式中出现多次,那么进行反向传播的时候就要非常小心。
考虑一个复杂函数
如果我们直接按计算线路图计算值的话,虽然也是能得到想要的结果,但是过程也同时相当繁琐的。
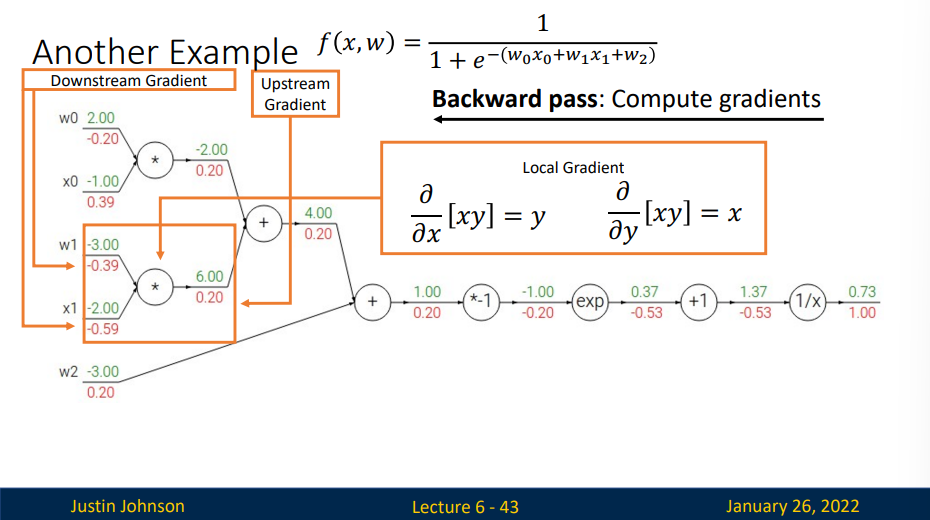 但我们注意到,这其中有一个sigmoid函数\(\sigma(x)=\frac{1}{1+e^x}\),事实上,对于sigmodi函数
但我们注意到,这其中有一个sigmoid函数\(\sigma(x)=\frac{1}{1+e^x}\),事实上,对于sigmodi函数
所以,将其中一部分计算流程当作模块化处理,方便我们进行计算。
几个门单元
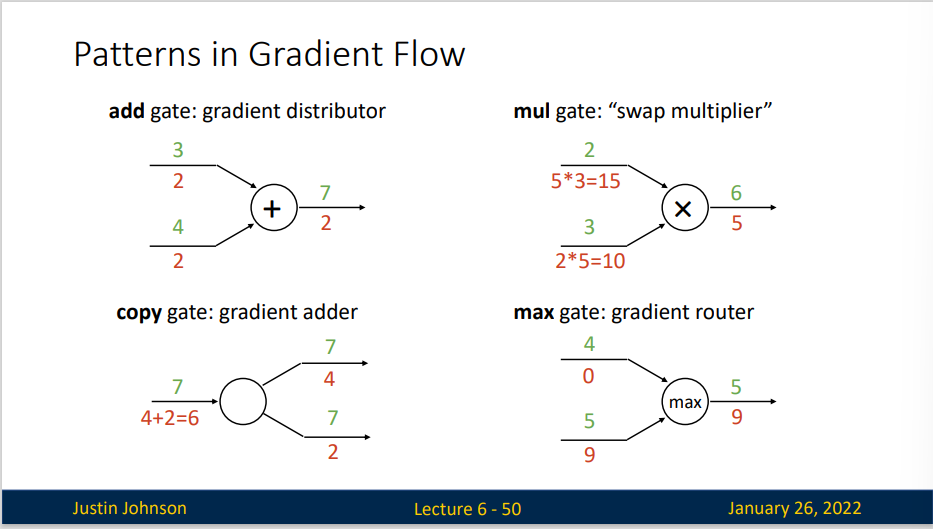
Vector-valued functions

那么在实际操作中,如何实现反向传播呢?下面这个是一个例子,我们从接收到的上游梯度(实际上是一个N*M的矩阵)
这个矩阵可以告诉我们,y对L的影响是什么样的