应力应变理论
应力分析
弹性体受力状态基本关系:
平衡关系
几何关系
物理关系
作用力:
\[
p = \lim_{\Delta V \rightarrow 0}\frac{\Delta P}{\Delta V} = \frac{dP}{dV}
\]
面力:作用在物体表面的分布力:风力、液体压力、两物体间的接触力
\[
T = \lim_{\Delta S \rightarrow 0}\frac{\Delta F}{\Delta S}=
\frac{d F}{dS}
\]
内力:在外界因素作用下的物体,其内部之间附加产生相互作用的一种量度
应力
根据连续性假设,假定微小面 \(\Delta S\) 上的力是连续分布的,则内力是这个分布力的合力,称 \(\frac{\Delta F}{\Delta S}\) 为平均应力,取 \(\Delta S\) 趋近于零,则可得应力:
\[
\begin{align}
f_n &= \lim_{\Delta S \rightarrow 0} \frac{\Delta F}{\Delta S} = \frac{d F}{dS}\\
& = f_{n1}e_1+f_{n2}e_2 + f_{n3}e_3\\
&= \sigma_n n+\tau_n \tau
\end{align}
\]
应力数值不仅依赖于空间点,而且依赖于微元面积的方向
应力张量
应力张量:
\[
(\sigma_{ij}) =\begin{bmatrix}
\sigma_{x} & \tau_{xy} & \tau_{xz}\\
\tau_{yx} & \sigma_{y} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_{z}
\end{bmatrix}= \begin{bmatrix}
\sigma_{11} & \sigma_{12} & \sigma_{13} \\
\sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{bmatrix}
\]
对于 \(\sigma_{ij}\) 第一个下标 \(i\) 表示所在面法向方向,第二个下标 \(j\) 表示应力方向。
做一个与坐标倾斜的微分面,斜面 \(n\) 上的应力矢量 \((f_{nx},f_{ny},f_{ny})\) ,当这个斜面无限接近 原点时,\((f_{nx},f_{ny},f_{ny})\) 可以表示过原点的任一微分面上的应力。
对于斜面上的应力,先考虑x方向上的平衡
\[
f_{nx}\Delta S_{abc}-\sigma_{x}\Delta S_{Obc}-\tau_{yx}\Delta S_{Oac}-\tau_{zx}\Delta S_{Oab} +\frac{1}{3}\Delta S_{abc}\delta h F_x =0
\]
由于体力\(\frac{1}{3}\Delta S_{abc} \delta hF_x\) 相较于应力为小量(多了一个\(\delta h\) ),忽略不计得
\[
f_{nx} = \sigma_x l +\tau_{yx}m+\tau_{zx}n
\]
其他方向的公式也可以导出
\[
\begin{align}
f_{nx} = \sigma_x l +\tau_{yx}m+\tau_{zx}n\\
f_{ny} = \tau_{xy} l +\sigma_{y}m+\tau_{zy}n\\
f_{nx} = \tau_{xz} l +\tau_{yz}m+\sigma_{z}n\\
\end{align}
\]
也称Cauthy's stress theorem(CST)公式。因此,如果知道一个点的 9 个应力分量,就能知道通过这个点的任意斜面的应力状态。
平衡方程
考虑一个微分平行六面体的平衡。假定 \(x=0\) 微分面上的应力分量 \(\sigma_x,\tau_{xy},\tau_{xz}\) 于是有泰勒展开得 \(x = dx\) 的微分面上的应力分量为
\[
\sigma_x +\frac{\partial \sigma_x}{\partial x}dx,\tau_{xy}+\frac{\partial\tau_{xy}}{\partial y}dy,\tau_{xz}+\frac{\partial \tau_{xz}}{\partial z}dz
\]
由 \(x\) 方向上的静力平衡方程可得
\[
\frac{\partial \sigma_{x} }{\partial x } + \frac{\partial \tau_{xy} }{\partial y } + \frac{\partial \tau_{xz} }{\partial z } + F_{x} = 0
\]
由此可以递推得到如下平衡微分方程:
\[
\begin{align}
&\frac{\partial \sigma_x}{\partial x} + \frac{\partial\tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z}+F_x = \rho \frac{\partial^2u}{\partial t^2}\\
&\frac{\partial \tau_{xy}}{\partial x} + \frac{\partial\sigma_{y}}{\partial y}+\frac{\partial \tau_{zy}}{\partial z}+F_x = \rho \frac{\partial^2v}{\partial t^2}\\
&\frac{\partial \tau_{xz}}{\partial x} + \frac{\partial\tau_{yx}}{\partial y}+\frac{\partial \sigma_{z}}{\partial z}+F_x = \rho \frac{\partial^2w}{\partial t^2}
\end{align}
\]
也称纳维方程,其中,\(F_x,F_y,F_z\) 表示单位体积的体力在3个坐标方向的分量,\(\rho\) 代表物体的密度, \(u,v,w\) 表示物体任一点的位移矢量在3个坐标方向的分量,上述方程考虑了物体运动情况,也就是引入了惯性力,当物体静止或做匀速运动时,惯性力为 0 。
张量形式:
\[
\sigma_{ij,j}+F_i = \rho \frac{\partial^2 u_i}{\partial t^2}
\]
\(\sigma_{ij,j}\) 表示应力分量对坐标的偏导数。
考虑力矩平衡可得关系
\[
\sigma_{ij} = \sigma_{ji}
\]
也就是切应力互等关系(应力张量对称性)。因此九个应力分量中只有六个分量是独立的
Note
基本弹性体不考虑力偶作用。对于部分材料,当研究微结构时需要考虑力偶作用,此时切应力互等失效,理论:couple stress theory
诺特定理
对于每个局部作用下的可微对称性,存在一个对应的守恒流。(每个对称性对应一种守恒律)
边界条件
从一个微分四面体推出应力边界条件,设单位面积上的外加面力的3个分量 \(\overline{f}_x,\overline{f}_y,\overline{f}_z\) ,表面外法线 \(n=(l,m,n)\) ,由CST公式可以推出应力边界条件
应力边界条件:
\[
\begin{align}
&\overline{f}_x = \sigma_{x} l +\tau_{yx}m+\tau_{zx}n\\
&\overline{f}_y = \tau_{xy} l +\sigma_{y}m+\tau_{zy}n\\
&\overline{f}_z = \tau_{xz} l +\tau_{yz}m+\sigma_{z}n
\end{align}
\]
也可以简写做
\[
\overline{f}_i = \sigma_{ij}n_j
\]
平衡微分方程对应物体内部的平衡,应力边界条件对应物体边界部分的平衡。如果物体是平衡的,则应力分量满足平衡微分方程和应力边界条件;反之,如已知应力分量满足平衡微分方程和应力边界条件,则物体也是平衡的,但这属于静力学上可能的平衡,对真实变形物体而言,还需考虑几何连续条件。
变换规则
当坐标系仅作平移变换,同一点的各应力分量是不会改变的。
考虑转轴变换,关系式
\[
\sigma_{i'j'} = \sigma_{ij}n_{i'i}n_{j'j}
\]
当坐标作转轴变换时,应力分量遵循二阶张量的变换规律,因此,这9个量组成二阶张量。显然,虽然转轴后各应力分量都改变了,但9个分量作为一个“整体”,所描绘的一点的应力状态是不会改变的
主应力理论
寻找某一坐标系,其中应力张量只有正应力分量,而切应力分量为零,即存在三个相互垂直的微分面,其上只有正应力而无切应力
由矢量分解有:
\[
f_{nx} = \sigma l, f_{ny} = \sigma m,f_{nz} = \sigma n
\]
主平面相对原坐标轴是一个倾斜的微分面,所以由柯西斜面公式得,
\[
\begin{align}
&f_{nx} = \sigma_x l +\tau_{yx}m+\tau_{zx}n\\
&f_{ny} = \tau_{xy} l +\sigma_{y}m+\tau_{zy}n\\
&f_{nz} = \tau_{xz} l +\tau_{yz}m+\sigma_{z}n
\end{align}
\]
带入可得
\[
\begin{align}
&(\sigma_x-\sigma) l +\tau_{yx}m+\tau_{zx}n=0\\
& \tau_{xy} l +(\sigma_{y}-\sigma)m+\tau_{zy}n=0\\
&\tau_{xz} l +\tau_{yz}m+(\sigma_{z}-\sigma)n=0
\end{align}
\]
满足有解的条件为
\[
\begin{vmatrix}
\sigma_x-\sigma& \tau_{yx} &\tau_{zx}\\
\tau_{xy}&\sigma_y-\sigma&\tau_{xy}\\
\tau_{xz}&\tau_{yz} &\sigma_z-\sigma
\end{vmatrix}=0
\]
展开后得到应力状态特征方程:
\[
\sigma^3-I_1\sigma^2+I_2\sigma - I_3=0
\]
其中
\[
\begin{align}
&I_1= \sigma_x+\sigma_y+\sigma_z\\
&I_2 = \sigma_y \sigma_z + \sigma_x \sigma_z +\sigma_x \sigma_y -\tau^2_{yz} - \tau^2_{xz}+\tau^2_{xy}\\
&I_3=
\begin{vmatrix}
\sigma_x& \tau_{yx} &\tau_{zx}\\
\tau_{xy}&\sigma_y&\tau_{xy}\\
\tau_{xz}&\tau_{yz} &\sigma_z
\end{vmatrix}
\end{align}
\]
称为应力张量不变量,其含义是:当坐标系旋转时,每个应力分量都要随之改变,但这3个量是不变的。方程的跟代表主应力,他的大小和方向在物体的形状和引起内力的因素确定以后是完全确定的,不随坐标的改变而改变。
对于解 \(\sigma_1,\sigma_2,\sigma_3\) 有三种情形
\(\sigma_1\neq \sigma_2\neq\sigma_3\neq \sigma_1\) ,三个应力主方向相互垂直\(\sigma_1=\sigma_2\neq\sigma_3\) \(\sigma_3\) 的方向垂直于 \(\sigma_1\) 和 \(\sigma_2\) 的方向,\(\sigma_1=\sigma_2=\sigma_3\) ,任何方向都是主应力方向
寻找切应力最大的微分面。
\[
f_{vx} = \sigma_1l,f_{vy} =\sigma_2m,f_{vz} =\sigma_3n
\]
用\(f_v\) 表示此微分面上应力矢量大小,\(\sigma_v,\tau_v\) 分别表示正应力与切应力
\[
\begin{align}
&f_v = \sqrt{f^2_{vx}+f^2_{vy}+f^2_{vz}}= \sqrt{\sigma_1^2l^2+\sigma_2^2m^2+\sigma_3^2n^2}\\
&\sigma_v=f_{vx}l+f_{vy}m+f_{vz}n =\sigma_1l^2+\sigma_2n^2+\sigma_3n^2
\end{align}
\]
于是有
\[
\begin{align}
\tau_v^2&=f^2_v-\sigma^2_v\\
&=\sigma_1^2l^2+\sigma_2^2m^2+\sigma_3^2n^2-(\sigma_1l^2+\sigma_2n^2+\sigma_3n^2)^2
\end{align}
\]
\(\sigma_1\neq \sigma_2\neq \sigma_3\)
\[
\begin{align}
&\tau_1= \pm\frac{\sigma_2-\sigma_3}{2}\\
&\tau_2= \pm\frac{\sigma_3-\sigma_1}{2}\\
&\tau_3= \pm\frac{\sigma_1-\sigma_2}{2}\\
\end{align}
\]
\(\sigma_1 = \sigma_3>\sigma_2\)
\[
\tau_v=\tau_3=\pm \frac{\sigma_1-\sigma_2}{2}
\]
\(\sigma_1 = \sigma_2= \sigma_3\) 没有切应力
应变分析
应变分析是几何分析,适用于一切连续介质
位移与应变
物体变形前后同一质点的位置矢量差:
\[
\mathbf{u} = \mathbf{\rho}(\xi,\eta ,\zeta)-\mathbf{r}(x,y,z)
\]
可以写出位移分量:
\[
\begin{align}
u = \mathbf{\rho}_1(\xi,\eta ,\zeta)-r_1(x,y,z)\\
v = \mathbf{\rho}_2(\xi,\eta ,\zeta)-r_2(x,y,z)\\
w = \mathbf{\rho}_3(\xi,\eta ,\zeta)-r_3(x,y,z)\\
\end{align}
\]
这三个量表示了一个点在坐标系的\(x,y,z\) 的位移分量
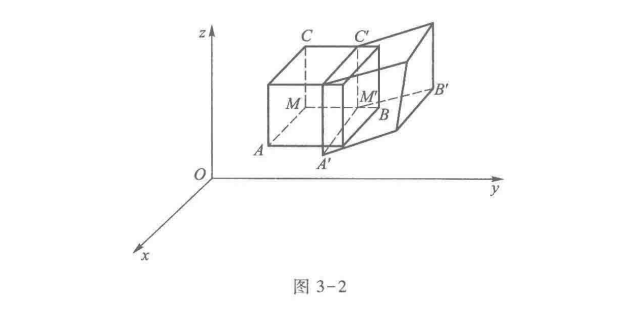
取一个六面微元体,正应变对应棱边的伸长,且应变对应棱边间夹角的变化
考虑小变形,我们给出正应变和切应变的表达式
\[
\begin{align}
\varepsilon_x = \frac{M'A'-MA}{MA},\gamma_{yz} = \frac{\pi}{2}-\angle C'M'B'\\
\varepsilon_y = \frac{M'B'-MB}{MB},\gamma_{xz} = \frac{\pi}{2}-\angle C'M'A'\\
\varepsilon_z = \frac{M'C'-MC}{MC},\gamma_{xy} = \frac{\pi}{2}-\angle A'M'B'\\
\end{align}
\]
这六个分量称为应变分量。
我们所考虑的是小变形,我们可以认为物体内各点的位移全由它自己的大小和形状的变化引起,忽略物体位置变化影响。
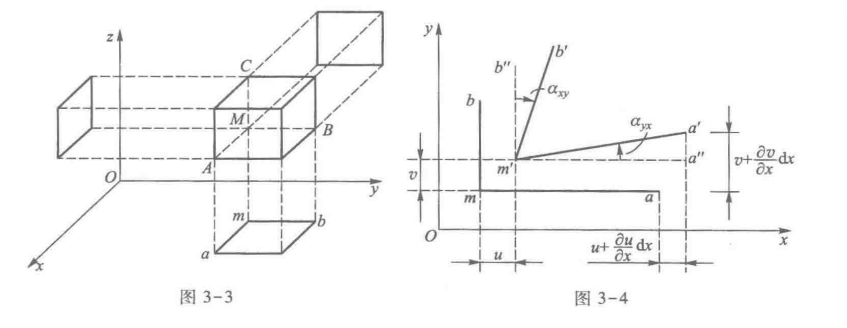
接下来建立应变分量和位移分量之间的关系。将我们的微分平行六面体分别投影到3个坐标平面。也就是如下图。
我们考虑 \(Oxy\) 平面上投影的变形。假定\(ma,mb\) 表示 \(MA,MB\) 在 \(Oxy\) 平面上的投影,\(m'a',m'b'\) 表示变形后 \(M'A',M'B'\) 在 \(Oxy\) 平面上的投影,所以A点位移表示为 \(u(x+dx,y,z),v(x+dx,y,z)\) , B点位移表示为\(u(x,y+dy,z),v(x,y+dy,z)\) ,其泰勒展开结果已在图中给出。取 \(m'a'\) 在\(Ox\) 轴上的投影 \(m'a''\) ,有
\[
m'a'' =dx+u+\frac{\partial u}{\partial x} dx -u = dx+ \frac{ \partial u}{\partial x}dx \approx M'A'
\]
于是正应变分量为
\[
\varepsilon_x= \frac{M'A'-MA}{MA} \approx \frac{dx + \frac{\partial u}{\partial x}dx - dx}{dx } = \frac{\partial u}{\partial x}
\]
同理有
\[
\varepsilon_y = \frac{\partial v}{\partial y} , \varepsilon_z = \frac{\partial w}{\partial z}
\]
我们得到了过物体内任意点并分别与3个坐标轴平行的微分线段的伸长率——正应变,接下来讨论切应变。
令 \(\alpha_{yx}\) 表示与 \(Ox\) 轴平行的微分线段 \(ma\) 向 \(Oy\) 轴转过的角度,\(\alpha_{yx}\) 表示与 \(Ox\) 轴平行的微分线段 \(mb\) 向 \(Ox\) 轴转过的角度,导出切应变分量:
\[
\gamma_{xy}= \frac{\pi}{2}- \angle B'M'A' \approx \frac{\pi}{2}-\angle b'm'a' = \alpha_{xy}+\alpha_{yx}
\]
有几何关系有
\[
\alpha_{yx} = \tan \alpha_{yx}= \frac{a'' a'}{m'a''} = \frac{\frac{\partial v}{\partial x}}{1+\frac{\partial u}{\partial x}}
\]
\(\frac{\partial u}{\partial x}\) 相比1是小量可以忽略,所以
\[
\alpha_{yx}= \frac{\partial v}{\partial x}
\]
同理可得 \(\alpha_{xy}\) 表达式
因此,切应变分量为
\[
\gamma_{xy}= \frac{\partial v}{\partial x}+ \frac{\partial u}{\partial y}
\]
其他方向上的切应变分量可由顺次轮换得到。
整理我们所得结果
\[
\begin{align}
&\varepsilon_{x} = \frac{\partial u}{\partial x}, \gamma_{yz} = \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}\\
&\varepsilon_{y} = \frac{\partial v}{\partial y}, \gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\\
&\varepsilon_{z} = \frac{\partial w}{\partial z}, \gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\\
\end{align}
\]
称为几何方程,又称柯西方程
相对位移张量:
\[
\begin{bmatrix}
\frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\
\frac{\partial v}{\partial x}&\frac{\partial z}{\partial y}&\frac{\partial v}{\partial z}\\
\frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z}\\
\end{bmatrix}
\]
对于单连通物体(无孔洞),若已知其相对位移张量,并假设位移分量具有二阶或二阶以上的连续偏导数,则可以通过积分求得连续单值的位移分量。也就是说,相对位移张量确定了物体变形情况。
我们可以将相对位移张量分解成如下形式(对称矩阵+反对称矩阵):
\[
\begin{align}
\begin{bmatrix}
\frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\
\frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}&\frac{\partial v}{\partial z}\\
\frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z}
\end{bmatrix} =
&\begin{bmatrix}
\frac{\partial u}{\partial x}&\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})&\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\\
\frac{1}{2}(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y})&\frac{\partial v}{\partial y}&\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\\
\frac{1}{2}(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z})&\frac{1}{2}(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})&\frac{\partial w}{\partial z}
\end{bmatrix}\\&
+\begin{bmatrix}
0&\frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x})&\frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})\\
\frac{1}{2}(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})&0&\frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y})\\
\frac{1}{2}(\frac{\partial w}{\partial x}-\frac{\partial u}{\partial z})&\frac{1}{2}(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z})&0
\end{bmatrix}
\end{align}
\]
定义
\[
\varepsilon_{ij} = \frac{1}{2}(u_{i,j}+u_{j,i})
\]
\[
\omega = \nabla \times \mathbf{u}=\begin{cases}
\omega_x= \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\\
\omega_y= \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\\
\omega_z= \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\\
\end{cases}
\]
其中 \(\omega\) 称为转动矢量,那么我们可以进一步改写表达式为
\[
\begin{align}
\begin{bmatrix}
\frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\
\frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}&\frac{\partial v}{\partial z}\\
\frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z}
\end{bmatrix} =
&\begin{bmatrix}
\varepsilon_{x}& \varepsilon_{xy} &\varepsilon_{xz}\\
\varepsilon_{yx}& \varepsilon_{y} &\varepsilon_{yz}\\
\varepsilon_{zx}& \varepsilon_{zy} &\varepsilon_{z}
\end{bmatrix}\\&
+\begin{bmatrix}
0& -\frac{1}{2}\omega_z &\frac{1}{2}\omega_y\\
\frac{1}{2}\omega_z& 0 &-\frac{1}{2}\omega_x\\
-\frac{1}{2}\omega_y& \frac{1}{2}\omega_x &0
\end{bmatrix}
\end{align}
\]
对于转动矢量,它代表微元体的刚性转动,是坐标的函数,对整个物体来说是变形的一部分。转动分量和应变分量一起完整地描述了物体的变形
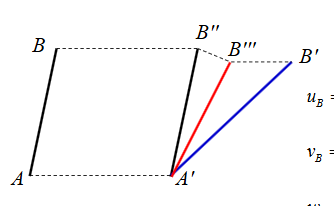
那么对于一个靠近A点的点B来说,变形所引起的位移有如下公式给出
\[
\mathbf{u}_B = \mathbf{u}+ \varepsilon d\mathbf{x}+ \omega d\mathbf{x}
\]
它包含三个部分
随A点的平移位移
绕A点刚性转动产生的位移
由A点邻近的微元体的变形在B点引起的位移。变形包括正应变与切应变,切应变带来转动
体应变
考察 \(dx,dy,dz\) 的微分平行六面体,变形前体积:
\[
V = dxdydz
\]
变形后体积
\[
\begin{align}
V^* &= dx(1+\varepsilon_x)dy(1+\varepsilon_{y})dz(1+\varepsilon_{z})\\
&\approx dxdydz(1+\varepsilon_{x}+\varepsilon_{y}+\varepsilon_{z})
\end{align}
\]
所以可得体应变表达式:
\[
\theta = \frac{V^*-V}{V} = \varepsilon_{x}+\varepsilon_{y}+\varepsilon_{z}
\]
也就是第一主变量的表达式,存在下面三种情况
\(\theta >0\) 微元体膨胀\(\theta<0\) 微元体收缩\(\theta =0\) 等容变形
应变协调方程
在我们引入应变协调方程之前,我们思考一个问题:如何从应变得到位移呢?因为我们知道,应变张量是由对位移求导得到的,那么我们就很自然的想到通过积分求得位移
\[
\int\frac{\partial u}{\partial x}dx+ \frac{\partial u}{\partial y}dy + \frac{\partial u}{\partial z}dz
\]
但是我们只知道 \(\frac{\partial u}{\partial x}\) ,而不知道直接知道其他两个分量。但是这两个分量实际上都是函数 ,我们对其求偏导便能用应变分量表示,比如说对于 \(\frac{\partial u}{\partial y}\)
\[
\begin{align}
&\frac{\partial}{\partial x}(\frac{\partial u}{\partial y}) = \frac{\partial }{\partial y}(\frac{\partial u}{\partial x} )= \frac{\partial \varepsilon_{x}}{\partial y}=A\\
&\frac{\partial}{\partial z}(\frac{\partial u}{\partial y})= \frac{\partial}{\partial y}(\gamma_{xy} - \frac{\partial v}{\partial x})=\frac{\partial \gamma_{xy}}{\partial y} -\frac{\partial \varepsilon_y}{\partial x} = B\\
&\frac{\partial}{\partial z}(\frac{\partial u}{\partial y}) = \frac{1}{2}[\frac{\partial}{\partial z}(\gamma_{xy}- \frac{\partial v}{\partial x}+\frac{\partial}{\partial z}(\gamma_{xz}- \frac{\partial w}{\partial x})] = \frac{1}{2}(-\frac{\partial \gamma_{yz}}{\partial x}+\frac{\partial \gamma_{xz}}{\partial y }+\frac{\partial \gamma_{xy}}{\partial z} ) =C
\end{align}
\]
利用积分
\[
\int Adx +Bdy +Cdz =0
\]
可以求得单值连续函数\(\frac{\partial u}{\partial y}\) ,然后按照这样的方法可以求得\(\frac{\partial u}{\partial z}\) ,最后求得 \(u\)
但是,为满足积分结果单值连续,我们给出条件
\[
\frac{\partial B}{\partial z} = \frac{\partial C}{\partial y},\frac{\partial A}{\partial z} = \frac{\partial C}{\partial x},\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}
\]
将 \(A,B,C\) 条件带入可求得关系,如果我们对每一个单值连续函数都做这样的处理,我们能得到18个条件,但只有6个是不同的,这六个条件也就是变形协调方程
回到最初的积分式子,当然,这是一个多元函数积分,微积分告诉我们这个积分结果可能是不唯一的,为了确保唯一性,我们也应当确保所积对象是单值连续函数(也就是积分与路径无关)。
此外,从数学角度上来说,柯西方程给出了包含六个方程却只有三个未知函数的偏微分方程,由于方程个数超过函数个数,方程组可能是矛盾的。
我们直接给出应变协调方程
\[
\begin{align}
&\frac{\partial^2 \varepsilon_z}{\partial y^2}+\frac{\partial^2 \varepsilon_y}{\partial z^2} = 2\frac{\partial^2\varepsilon_{yz}}{\partial y\partial z}\\
&\frac{\partial^2\varepsilon_x }{\partial z^2}+\frac{\partial^2 \varepsilon_z}{\partial x^2} = 2\frac{\partial^2 \varepsilon_{xz}}{\partial x\partial z}\\
&\frac{\partial^2 \varepsilon_y}{\partial x^2}+\frac{\partial^2 \varepsilon_x}{\partial y^2} = 2\frac{\partial^2 \varepsilon_{xy}}{\partial x\partial y}\\
&\frac{\partial}{\partial x}\left(-\frac{\partial\varepsilon_{yz} }{\partial x}+\frac{\partial \varepsilon_{xz}}{\partial y}+\frac{\partial \varepsilon_{xy}}{\partial z}\right) = \frac{\partial^2\varepsilon_x}{\partial y\partial z}\\
&\frac{\partial}{\partial y}\left(\frac{\partial \varepsilon_{yz}}{\partial x}-\frac{\partial \varepsilon_{xz}}{\partial y}+\frac{\partial \varepsilon_{xy}}{\partial z}\right) = \frac{\partial^2\varepsilon_y}{\partial x\partial z}\\
&\frac{\partial}{\partial z}\left(\frac{\partial \varepsilon_{yz}}{\partial x}+\frac{\partial \varepsilon_{xz}}{\partial y}-\frac{\partial \varepsilon_{xy}}{\partial z}\right) = \frac{\partial^2\varepsilon_z}{\partial x\partial y}
\end{align}
\]
又称圣维南方程,这是保证物体连续的一个必要条件
张量形式:
\[
\varepsilon_{ij,kl}e_{ikm}e_{jln}=0
\]
用应变导数表示
如果物体时单连通的,则应变分量满足应变协调方程也是物体连续的充分条件
而多联通物体,总是可以作适当的截面使它变成单连通物体,在此被割开以后的区域里,一定能求得单值连续的函数 \(u,v,w\) 。但对于求得的 \(u,v,w\) ,当点 \((x,y,z)\) 分别从截面两侧趋向于截面上某一点时,他们将趋于不同的值 \(u^+,v^+,w^+,u^-,v^-,w^-\) ,为满足连续条件,需添加补充条件
\[
u^+=u^-,v^+=v^-,w^+=w^-
\]
此时应变协调方程也是充分条件。