Neural Networks
约 2176 个字 13 张图片 预计阅读时间 15 分钟
Problem: Linear Classifiers aren't that powerful

对于几何视角,线性分类器的行为更像是将高维的欧氏空间分割成两个子空间,但是有些时候,我们的数据无法被线性分类器直接分类。
而对于视觉角度,我们认为线性分类器只为每个类别学习一个模板,但是线性分类器无法识别一个类别的多种模式。
Feature Transform
于是我们引入一个方法:特征变换(Feature Transforms)
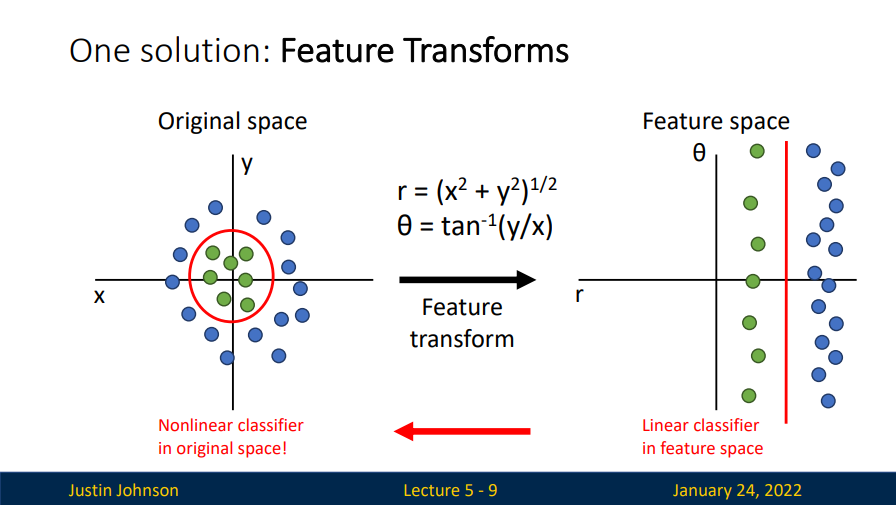
这是一个将笛卡尔坐标系变换到极坐标系的例子,原本在笛卡尔坐标系下线性不可分的数据集,变换后在极坐标系下线性可分了,也就是说我们可以在特征空间下构建线性分类器。
还有一种进行图像特征提取的方式就是定向梯度直方图。
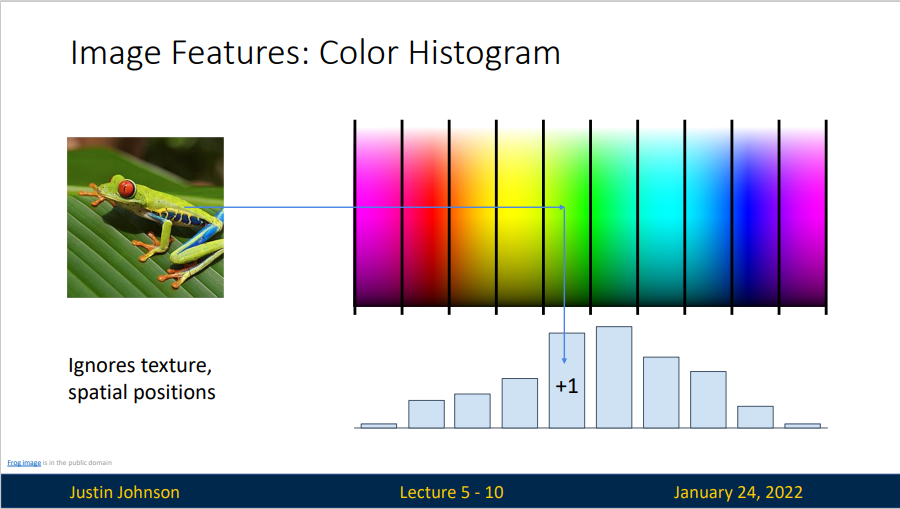
- Compute edge direction / strength at each pixel
- Divide image into 8x8 regions
- Within each region compute a histogram of edge directions weighted by edges strength

Neural Networks
一个二层神经网络的模型
Learnable parameters: \(W_1\in \mathbb{R}^{H\times D},b_1\in \mathbb{R}^{H},W_2\in \mathbb{R}^{C\times D},b_2\in \mathbb{R}^{C}\)
In pratcie we will usually add a learnable bias at each layers as well.
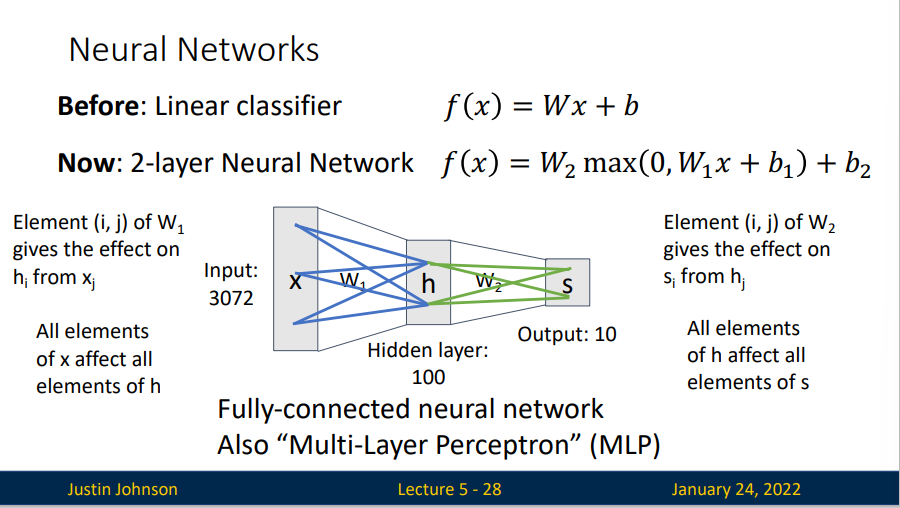
\(W_1\)的作用是将图像转换成一个100为的过度向量,函数\(\max(0,-)\)是非线性的,它会作用到每个元素,这个非线性函数有多种选择,这个形式是最常用的选择,它就是简单地设置阈值,将所有小于0的值变成0.最终再经历\(W_2\)的处理得到10个数字,这10个数字可以解释为是分类的评分。
那么,一个三层神经网络也可以类比看作\(W_3\max(0,W_2\max(0,W_1x+b_1)+b_2)+b_3\),其中\(W_1,W_2,W_3\)需要进行学习的参数。中间隐层的尺寸是网络的超参数。
非线性函数也称为激活函数。激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活, 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。 由于激活函数是深度学习的基础。

ReLU函数 最受欢迎的激活的激活函数是修正线性单元(ReLU),它实现简单,同时在各种预测任务中表现良好。使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。 这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)。 变体:
sigmoid函数 对于一个定义域在\(\mathbb{R}\)中的输入, sigmoid函数 将输入变换为区间(0, 1)上的输出。 因此,sigmoid通常称为 挤压函数(squashing function): 它将范围\((-\inf, \inf)\)中的任意输入压缩到区间\((0, 1)\)中的某个值:
在最早的神经网络中,科学家们感兴趣的是对“激发”或“不激发”的生物神经元进行建模。 因此,这一领域的先驱可以一直追溯到人工神经元的发明者麦卡洛克和皮茨,他们专注于阈值单元。 阈值单元在其输入低于某个阈值时取值0,当输入超过阈值时取值1。
当人们逐渐关注到到基于梯度的学习时, sigmoid函数是一个自然的选择,因为它是一个平滑的、可微的阈值单元近似。 当我们想要将输出视作二元分类问题的概率时, sigmoid仍然被广泛用作输出单元上的激活函数 (sigmoid可以视为softmax的特例)。 然而,sigmoid在隐藏层中已经较少使用, 它在大部分时候被更简单、更容易训练的ReLU所取代。 在后面关于循环神经网络的章节中,我们将描述利用sigmoid单元来控制时序信息流的架构。
tanh函数 与sigmoid函数类似,tanh(双曲正切)函数也能将其输入压缩转换到区间\((-1,1)\)。
Neurons
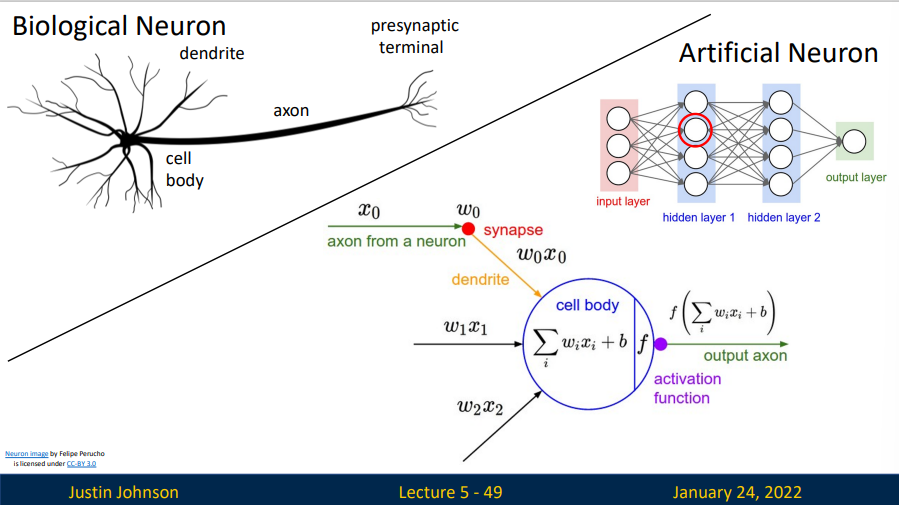
对于生物的神经元,每个神经元都从它的多个树突(dendrite)获得输入信号,然后沿着它唯一的轴突(axon)产生输出信号。轴突在末端会逐渐分枝,通过突触和其他神经元的树突相连。
因此,借鉴生物神经系统,建立了神经元计算模型。在该模型中,沿着轴突传播的信号将基于突触的突触强度,与其他神经元的树突进行乘法交互。其观点是,突触的强度(也就是权重 \(w_i\)),是可学习的,且可以控制一个神经元对于另一个神经元的影响强度(还可以控制影响方向:使其兴奋(正权重)或使其抑制(负权重))。在基本模型中,其他神经元的树突将信号(也就是输入 \(x_i\))传递到细胞体,信号在细胞体中相加(下图右侧的 \(\sum w_ix_i+b\))。如果最终之和高于某个阈值,那么神经元将会激活,向其轴突输出一个峰值信号(也就是一种非线性的输出)。在计算模型中,我们假设峰值信号的准确时间点不重要,是激活信号的频率在交流信息。基于这个_速率编码_的观点,将神经元的激活率建模为激活函数(activation function),它表达了轴突上激活信号的频率。
Space Warping
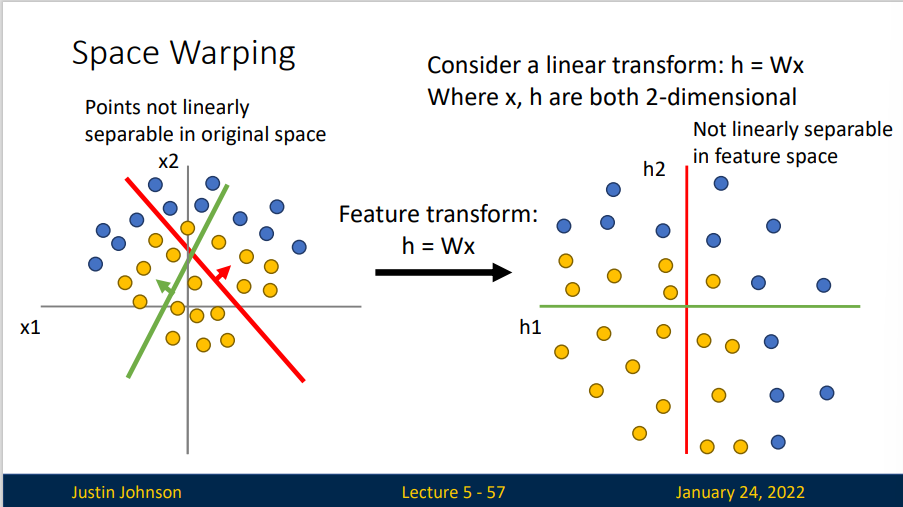
对于上方无法用超平面分割的数据集,我们找不到一个合适的变换矩阵\(W\)来分割。于是我们就需要一个非线性的方式来分割,也就是激活函数的方法。
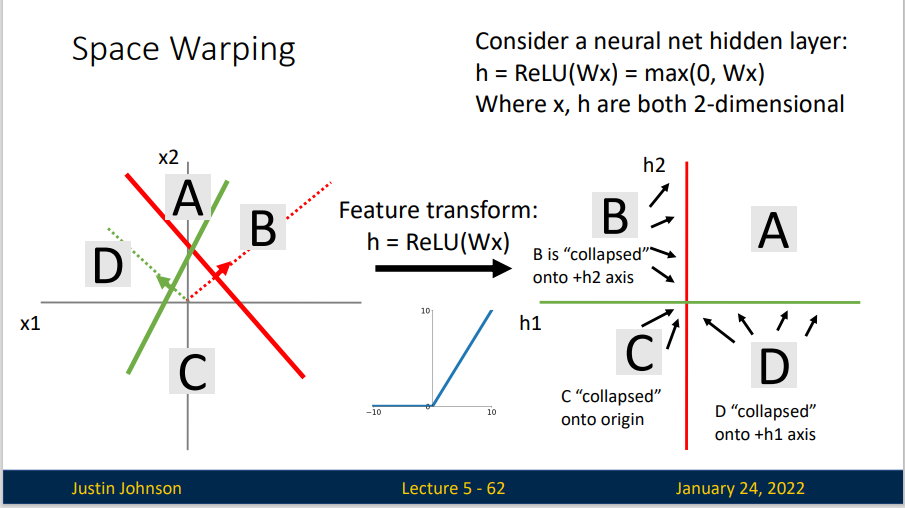
我们使用了两个ReLU激活函数,A区域内的数据仍对应变换后特征空间的A区域内的数据。而对于B和D区域内数据,变换后所对应的数据则落在坐标轴上,最后,对于C区域的数据,变换后他落在原点上。这样子,我们就对一个无法线性分割的数据集完成了一次分割。
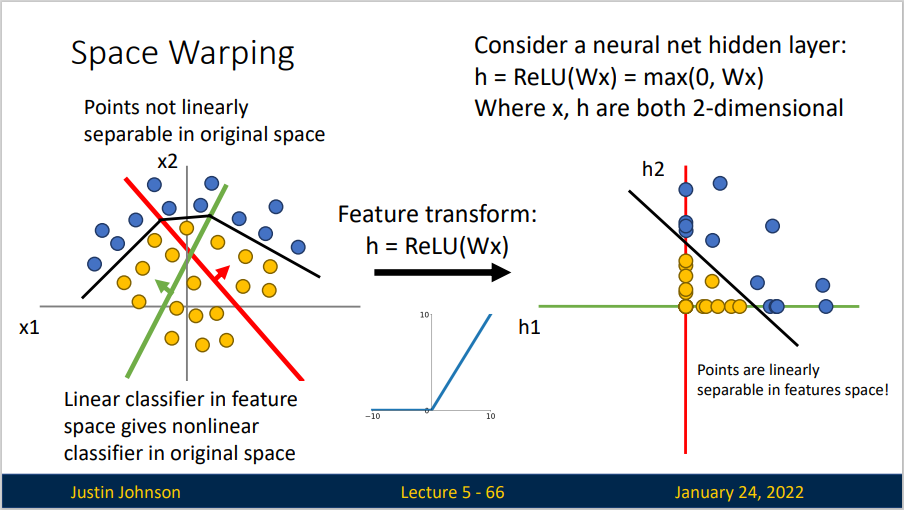
我们可以通过设定更多的隐藏层来进行更为复杂和精确的数据集划分,但这也会导致模型过拟合。为了防止过拟合,我们设置\(L_2\)惩罚项来保证拟合结果更为平滑。
设置\(L_2\)惩罚项来调整模型的方法也被称为权重衰减。 \(L_2\)正则化线性模型构成经典的岭回归(ridge regression)算法,使用\(L_2\)范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中,这可能使它们对单个变量中的观测误差更为稳定。
Universal Approximation
A neural network with one hidden layer can approximate any function \(f:R^N\rightarrow R^M\) with arbitrary precision

神经网络可以通过隐藏神经元,捕捉到输入之间复杂的相互作用,这些神经元依赖于每个输入的值。 我们可以很容易地设计隐藏节点来执行任意计算。 我们也可以用这种方法,设定足够的神经元和正确的权重以对任意函数建模,尽管实际中学习该函数是很困难的。
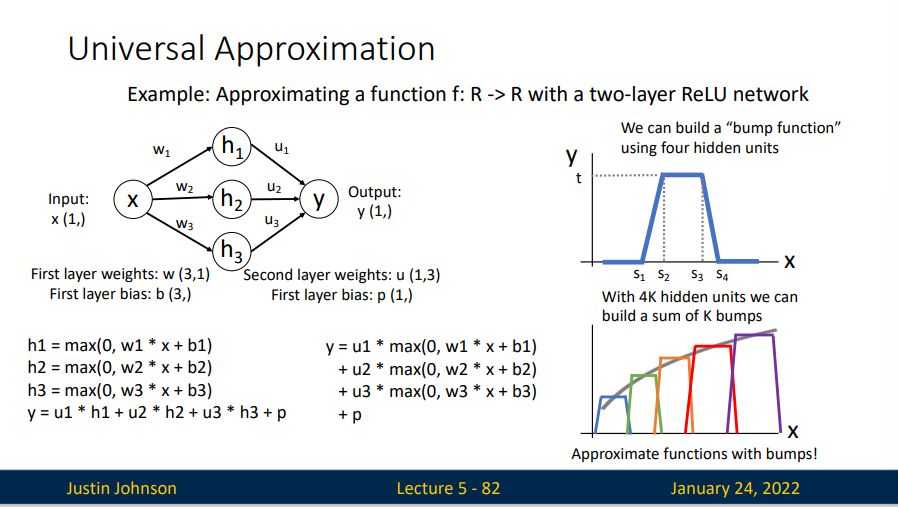
我们可以用四个神经元来建立一个"bump function",假定我们有4千个隐藏单元,我们可以建立一个1千个“bump function”,通过对这一千个bumps求和来拟合一个函数。
但是,事实上,神经网络并不会学习任何 bump 函数。
Universal approximation tells us: - Neural nets can represent any function
Universal approximation DOES NOT tell us: - Whether we can actually learn any function with SGD - How much data we need to learn a function
Convex Functions
A function \(f :X \subseteq \mathbb{R}^N \rightarrow \mathbb{R}\) is convex if for all \(x_1,x_2 \in X, t\in [0,1]\)
A convex function is a (multidimensional) bow
Generally speaking, convex functions are easy to optimize: can derive theoretical guarantees about converging to global minimum
Most neural networks need nonconvex optimization - Few or no guarantees about convergence - Empirically it seems to work anyway - Active area of researc
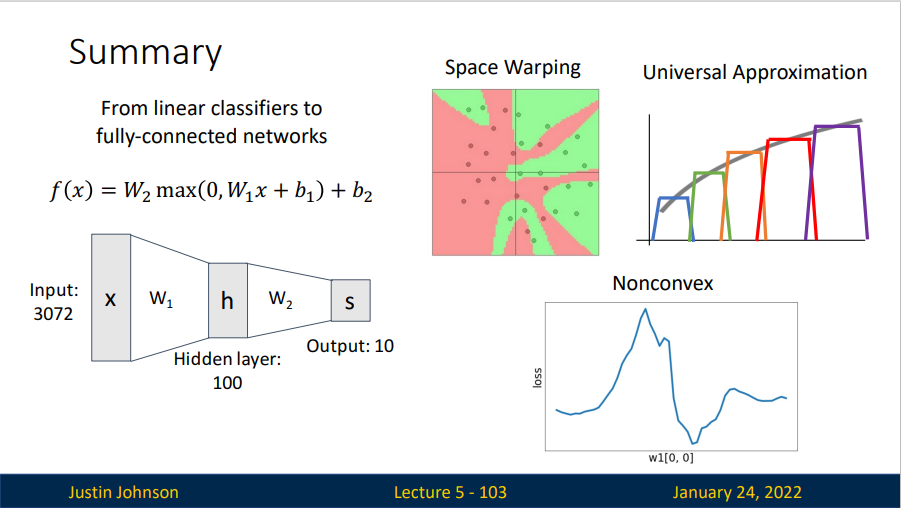
Summary